A 2000 áprilisi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 227. Létezik-e olyan pozitív egész n, hogy tetszőleges nem 0 i számjegy esetén az n, 2n, 3n, ..., 2000n számok mindegyikének tízes számrendszerbeli alakjában ugyanannyiszor fordul elő az i?

Megoldásvázlat. Példát mutatunk olyan n pozitív egész számra, amelyre tetszőleges 0-tól különböző i számjegy esetén az n, 2n, ..., 65536n mindegyikének tízes számrendszerbeli alakjában az i pontosan ugyanannyiszor fordul elő.

Legyen p=2¹⁶+1=65537. (Mint ismeretes, ez a szám prím.) Először bebizonyítjuk, hogy a 10 primitív gyök modulo p, vagyis az 1, 10, 10², ..., 10^p-2 számokat p-tel osztva az 1, 2, ..., 65536 maradékok egyszer-egyszer fordulnak elő.

A Fermat-tétel alapján 10²¹⁶=10^p-11 (mod p), ezért a legkisebb k szám, amire 10^k1 (mod p), osztója a p-1=2¹⁶-nak, azaz 2-hatvány. (Ezt a k kitevőt hívják a 10 rendjének modulo p.) Nem nehéz ellenőrizni, hogy

10²³-9462 (mod p),
10²⁴=(10²³)²9462²5902 (mod p),
10²⁵=(10²⁴)²5902²-32080 (mod p),
10²⁶=(10²⁵)²32080²-1111 (mod p),
10²⁷=(10²⁶)²1111²-10882 (mod p),
10²⁸=(10²⁷)²10882²-7435 (mod p),
10²⁹=(10²⁸)²7435²31534 (mod p),
10²¹⁰=(10²⁹)²31534²255 (mod p),
10²¹¹=(10²¹⁰)²255²-512 (mod p),
10²¹²=(10²¹¹)²512²-4 (mod p),
10²¹³=(10²¹²)²4²16 (mod p),
10²¹⁴=(10²¹³)²16²256 (mod p),
10²¹⁵=(10²¹⁴)²256²-1 (mod p).

Vagyis a 10 rendje nem lehet 2¹⁶-nál kisebb. Mivel k=p-1, az 1, 10, 10², ..., 10^p-2 számok csupa különböző maradékot adnak p-vel osztva, vagyis az összes 0-tól különböző maradékot kiadják.

Eredményünk egyik következménye, hogy az 1/p - tiszta szakaszos - tizedestört alakja p-1 hosszúságú periódusokból áll. Legyen n az a szám, amit az első p-1 tizedesjegy összeolvasásával kapunk, tehát n=(10^p-1-1)/p. Azt állítjuk, hogy ez a választás megfelelő.

Legyen 1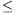k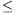p-1 tetszőleges egész. Mivel a 10 primitív gyök, létezik egy olyan l kitevő, amelyre 10^lk (mod p.

A k/p és 10^l/p számok tört része megegyezik. A k/p tizedestört alakjának első p-1 jegyét, az első periódust összeolvasva a kn számot kapjuk. Másrészt 10^l/p tizedesjegyei ugyanazok, mint 1/p tizedesjegyei, csak l hellyel balra csúsztatva. Ebből következik, hogy kn tízes számrendszerbeli felírásában pontosan ugyanazok a számjegyek vannak, mint n felírásában, ciklikusan felcserélve.

A. 236. Egy háromszög területe t, oldalai a<b<c, a hozzájuk tartozó súlyvonalak hossza rendre s_a, s_b, s_c. Bizonyítsuk be, hogy

4acs_as_c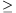16t²+(b²-a²)(c²-b²).

Megoldásvázlat.

A Héron-képletből t²=-a⁴+2a²b²+2a²c²-b⁴+2b²c²-c⁴; továbbá ismeretes, hogy 4s_a²=-a²+2b²+2c² és 4s_c²=2a²+2b²-c². Ezeket beírva, négyzetre emelve és rendezve a következő egyenlőtlenséget kapjuk:

-a⁸+6a⁶b²-13a⁴b⁴+2a⁴b²c²+2a⁴c⁴+12a²b⁶-10a²b⁴c²+

2a²b²c⁴-4b⁸+12b⁶c²-13b⁴c⁴+6b²c⁶-c⁸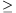0.

A baloldal szorzattá alakítható:

(a²-2b²+c²)²(-a⁴+2a²b²+2a²c²-b⁴+2b²c²-c⁴)0

azaz

(a²-2b²+c²)²t²0.

Megjegyzés. Egyenlőség akkor áll, ha a²+c²=2b². A B.3360. feladat szerint ez azzal ekvivalens, hogy az a és c oldalak valamint az ezekhez tartozó súlyvonalak által közrezárt négyszög húrnéngyszög.

A feladat valójában fordított módon "készült": a négyszögre felírtuk a Ptolemaiosz tétel általánosabb változatát. (Ha egy négyszög oldalai a, b, c és d, átlói e és f, akkor ac+bdef, és egyenlőség akkor áll, ha a négyszög húrnégyszög.) Ezt az egyenlőtlenséget rendezve kaptuk a feladatban kitűzött egyenlőtlenséget.

A. 237. Egy konvex n-szögnek megrajzoltuk kn+1 különböző átlóját (n és k pozitív egészek). Igazoljuk, hogy a megrajzolt átlók közül kiválasztható 2k+1 olyan, amelyek egy töröttvonalat alkotnak, és közülük semelyik kettő nem metszi egymást.

Megoldásvázlat. A k szerinti teljes indukcióval bebizonyítjuk, hogy létezik olyan cikk-cakkban haladó töröttvonal, ami a feltételeknek megfelel, sőt mindkét irányú cikk-cakk létezik.

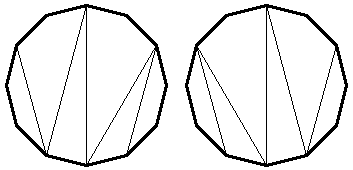
1. ábra

Állításunkat a triviális k=0 esetre is kiterjesztjük; ekkor az 1 behúzott átló közül kell egyet kiválasztanunk.

Tegyük fel, hogy az állítás igaz valamely k=m-re; ekkor a k=m+1 értékre is igazoljuk. Tegyük fel, hogy behúztunk összesen (m+1)n+1 átlót. Minden egyes csúcsnál, ahonnan legalább egy átlót behúztunk, rendezzük sorba az átlókat az óramutató járása szerint, és színezzük az első átlót pirosra:

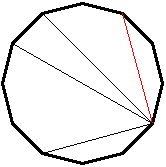
2. ábra

Legfeljebb n átlót színeztünk ki, van legalább mn+1 olyan átló, amit nem színeztünk ki. Ezek közül az indukciós feltevés szerint kiválasztható mindkét irányban egy-egy 2k+1 hosszúságú, cikk-cakkban haladó töröttvonal. Ezek közül vegyük az 1. ábra jobboldalán látható típusút. Ezt kiegészítve a végpontjainál kiszínezett piros élekkel, egy 2-vel hosszabb töröttvonalat kapunk:

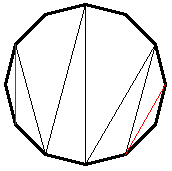
3. ábra

A másik fajta cikk-cakkot hasonlóan kapjuk.

A. 238. Legyen x pozitív valós szám és k pozitív egész. Bizonyítsuk be, hogy ha x^k+1/x^k és x^k+1+1/x^k+1 racionális, akkor x+1/x is racionális.

Megoldásvázlat. Ha x=1, akkor az állítás triviális. A továbbiakban feltételezzük, hogy x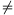1.

Legyen tetszőleges n egész számra 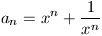. Azt kell igazolnunk, hogy ha a_k és a_k+1 racionális, akkor a₁ is racionális.

Behelyettesítéssel igazolható, hogy tetszőleges m, n egészekre

(1)    a_na_m=a_m+n+a_m-n.

Mivel a₀=2 racionális, az azonosságot az m=n,2n,3n,... választással felírva láthatjuk, hogy ha a_n racionális, akkor a_2n, a_3n, ... is mind racionális.

Tekintsük most az b₀=a₀, b₁=a_k, b₂=a_2k, b₃=a_3k, ... és a c₀=a₁, c₁=a_k+1, c₂=a_2k+1, c₃=a_3k+1, ... sorozatokat. Az (1) azonosság alapján ezekre teljesül, hogy b_m+1=a_kb_m-b_m-1 és c_m+1=a_kc_m-c_m-1; a két sorozatra tehát pontosan ugyanaz a rekurzív formula érvényes. Próbáljuk felírni c_m-et a következő alakban:

(2)    c_m=pb_m+qb_m+1,

ahol p és q alkalmas valós számok. Az m=0 és m=1 esetekben

a₁=pa₀+qa_k,

a_k+1=pa_k+qa_2k.

Ezt az egyenletrendszert megoldva

és

.

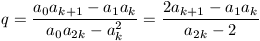(A nevezők pozitívak, mert a_2k>2. Ezeket beírva (2)-be a következő azonosságot kapjuk:

(a_2k-2)a_mk+1=(a₁a_2k-a_ka_k+1)a_mk+(2a_k+1-a₁a_k)a_(m+1)k,

vagy másképpen

(3)    (a_2k-2)a_mk+1 = (2a_(m+1)k-a_ka_mk)a_k+1-(a_ka_(m+1)k-a_2ka_mk)a₁ = (2a_(m+1)k-a_(m+1)k-a_(m-1)k)a_k+1-(a_(m+2)k+a_mk-a_(m+2)k-a_(m-2)k)a₁ = (a_(m+1)k-a_(m-1)k)a_k+1-(a_mk-a_(m-2)k)a₁.

Legyen most m=k+2. Ezzel a választással

(4)    (a_2k-2)a_(k+1)²=(a_(k+3)k-a_(k+1)k)a_k+1-(a_(k+2)k-a_k²)a₁.

Ebben az azonosságban a₁ kivételével mindegyik számról tudjuk, hogy racionális. Az a₁ együthatója pedig pozitív. Tehát a₁ is racionális.

Megjegyzés. Természetesen a (4) azonosság közvetlenül is ellenőrizhető.