A 2000. áprilisi B-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaLban folyamatosan közöljük.
B. 3362. Tizennyolc gyerek megoldotta a KöMaL áprilisi számának egy-egy feladatát. A megoldásokat elektronikus levelezéssel (e-mailen keresztül) akarják megbeszélni. Legalább hány e-mailt kell küldeniük egymásnak, hogy mindegyikük megtudja mindegyik megoldást? (Minden e-mail annyiszor számít, ahány embernek küldik.) (5 pont)
Gyanta Nándor ötletéből
Megoldásvázlat. Feltehető, hogy nem kapott két gyerek egyszerre levelet. Ekkor van egy olyan pillanat, amikor pontosan egy olyan gyerek van, aki mind a 18 megoldást ismeri. Ez előtt az állapot előtt biztos, hogy a többi gyerek elküldött legalább 1 levelet, és ez után pedig biztos, hogy mindenki kapott legalább 1 levelet. Ez összesen legalább 34 levél. Ennyi elég is, hiszen ha először mindenki elküldi ugyanannak a gyereknek az általa kidolgozott feladatot, majd ő az így összegyűjtött összes megoldást elküldi mindenkinek, akkor összesen 34 e-mailt küldtek egymásnak.
B. 3363. Van-e olyan háromszög, amit két vágással három egybevágó részre lehet darabolni? (3 pont)
Megoldásvázlat. Van:

B. 3364. Tegyük fel, hogy 15 különböző (pozitív) prímszám számtani sorozatot alkot. Igazoljuk, hogy a sorozat két szomszédos tagjának a különbsége 30000-nél nagyobb. (3 pont)
Székelyhidi Tamás 11. o.t., Budapest
Megoldásvázlat. Először azt bizonyítjuk be, hogy a sorozatban nem szerepel a 2, 3, ..., 13 prímek egyike sem. Ugyanis ha valamelyik szerepelne, akkor a sorozat első tagja (jelöljük p1-gyel) is a fenti prímek közül lenne az egyik. Ekkor viszont p1+p1d (ahol d a sorozat különbsége) is a sorozat tagja, pedig nem prím, ami nem lehet. Tehát a sorozat tagjai nagyobbak, mint 13. Második lépésként azt bizonyítjuk be, hogy d osztható az első hat prímmel, például 13-mal. p1, p1+d, p1+2d,..., p1+12d, amennyiben d nem többszöröse 13-nak, különböző maradékot adnak 13-mal osztva, tehát egyikük osztható 13-mal(de nem 13), és így nem lehet prím. Ugyanígy bizonyítható, hogy d osztható az első öt prímszámmal is. Tehát d osztható ezek szorzatával, 30030-cal, tehát biztosan nagyobb, mint 30000.
B. 3365. Bizonyítsuk be, hogy ha abc=1 és 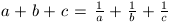 , akkor az a, b, c
számok közül legalább az egyik 1-gyel egyenlő. (3 pont)
, akkor az a, b, c
számok közül legalább az egyik 1-gyel egyenlő. (3 pont)
Gyanta Nándor, Budapest
Megoldásvázlat. Szorozzuk meg az egyenlet mindkét oldalát abc-vel! Mivel abc=1, a következő egyenlethez jutunk: a+b+c=bc+ac+ab. Ezt átalakítva abc-bc-ac-ab+a+b+c-1=0. A baloldalt szorzattá bontva (a-1)(b-1)(c-1)=0, amiből következik a feladat állítása.
B. 3366. Ismét útnak indul az F. 3279. feladat szöcskéje. Most egy r sugarú kör és egy, a kör középpontján át nem menő egyenes pontjai között ugrál, a körről az egyenesre, onnan pedig vissza a körre. Bizonyítsuk be, hogy r hosszúságú ugrásokkal legfeljebb 8 pontba juthat el. (5 pont)
Hraskó András, Budapest
Megoldásvázlat.
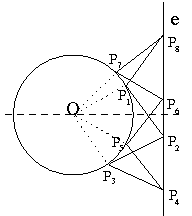
Feltehetjük, hogy ha a szöcske két helyre is ugorhat, akkor nem oda ugrik, ahonnnan jött. Legyen a szöcske kiindulási pontja P1, onnan ugorjon P2-re, és így tovább. Mivel az ugrások hossza r, ezért OP1P2P3 (esetleg elfajuló) rombusz. Hasonlóan OP3P4P5 is rombusz. Könnyen látható, hogy a P1OP5 háromszög és a P2P3P4 háromszög egymás eltoltjai, így P1P5||e. Ezért az O-ból e-re bocsájtott merőlegesre nézve P1 és P5 egymás tükörképei. (Ez az elfajuló esetekre is igaz.) Ha most a szöcske tovább ugrál P5-ből, hasonlóan belátható, hogy P5 és P9 is ugyanerre a merőlegesre egymás tükörképei, azaz P1 és P9 megegyeznek. Tehát a továbbiakban a szöcske már csak a P1,...,P8 pontok valamelyikére ugorhat.
Somogyi Dávid dolgozata alapján
B. 3367. Egy egyenlő szárú háromszög alakú papírlapot összehajtottunk úgy, hogy az alap A csúcsa a BC szár felezőpontjába került. Ekkor a hajtás élének egyik végpontja az AC szárat p:q arányban osztja. Milyen arányban osztja a hajtás élének másik végpontja az AB alapot? (5 pont)
A Magyar Hírlap nyomán
Megoldásvázlat.
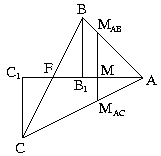
Jelölje BC felezőpontját F, AF felezőpontját
M. Legyen B ill. C merőleges vetülete
AF-re B1
ill. C1. Ha A-t
F-re hajtjuk, akkor a hajtási él AF felező
merőlegese. Legyen a hajtási él és AB ill. AC
metszéspontja MAB
ill. MAC. A párhuzamos
szelők tételének következménye miatt (C1F+FM):MA=CMAC:MACA=p:q= :1. Ezért C1F:MA=(
:1. Ezért C1F:MA=( -1):1. Mivel B1F=FC1, ezért BMAB:MABA=B1M:MA=(FM-FB1):MA=(FM-C1F):MA=1-(
-1):1. Mivel B1F=FC1, ezért BMAB:MABA=B1M:MA=(FM-FB1):MA=(FM-C1F):MA=1-( -1):1=2-
-1):1=2- :1=(2q-p):q. Tehát a hajtás
élének másik végpontja (2q-p):q arányban osztja
az AB alapot.
:1=(2q-p):q. Tehát a hajtás
élének másik végpontja (2q-p):q arányban osztja
az AB alapot.
Béky Bence dolgozata alapján
B. 3368. Hány megoldása van a pozitív egész számok körében az x7+y8=z9 egyenletnek? (4 pont)
Behm Andrea, Nagykanizsa
Megoldásvázlat. Például x=28(9n+4), y=27(9n+4), z=225+56n bármilyen n természetes szám esetén megoldást adnak, tehát végtelen sok megoldás van.
B. 3369. Egy tetraéder mindegyik élén kijelöljük az egyik harmadolópontot. Mekkora lehet az ezek által meghatározott konvex test és a tetraéder térfogatának hányadosa? (4 pont)
Megoldásvázlat. A harmadolópontok által meghatározott test térfogatát legegyszerűbben úgy határozhatjuk meg, hogy az eredeti tetraéder térfogatából levonjuk annak a négy kis tetraédernek a térfogatát, amelyeket az eredeti tetraéder egy-egy csúcsa, valamint az abból a csúcsból kiinduló három-három élen lévő harmadolópontok alkotnak.
Legyen az eredeti tetraéder térfogata 27 egység. Ekkor egy kis tetraéder térfogata 1, 2, 4 vagy 8 egység, attól függően, hogy az eredeti tetraéderrel közös csúcsából kiinduló élei közül 0, 1, 2 vagy 3 olyan van, amelyik az él 2/3 részével megegyező hosszúságú. Összesen 6 db 2/3 hosszú és 6 db 1/3 hosszú éle van a 4 kis tetraédernek. Könnyen belátható, hogy a következő 4 eset lehetséges:
- 1. Egy kis tetraéder térfogata 1, a többié 4 egység.
- 2. Egy kis tetraéder térfogata 1, egyé 2, egyé 4, egyé pedig 8 egység.
- 3. Három kis tetraéder térfogata 2, egyé pedig 8 egység.
- 4. Két kis tetraéder térfogata 2, másik kettőé pedig 4 egység.
A keresett arány értéke tehát 14/27, 12/27, 13/27 vagy 15/27.
B. 3370. A és B két véletlen esemény. Igazoljuk, hogy
|P(A.B)-P(A).P(B)| 1/4.
1/4.
(5 pont)
Megoldásvázlat.
A feladat megoldásához csak a legszükségesebbeket
kell tudni a valószínűségszámítás alapjaiból: egy A véletlen
esemény valószínűsége q P(A)
P(A) 1, és
P(AB) jelöli annak a valószínűségét, hogy A és
B egyszerre következnek be.
1, és
P(AB) jelöli annak a valószínűségét, hogy A és
B egyszerre következnek be.
I. Először belátjuk, hogy
P(AB)-P(A)P(B)
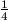 . Mivel 0
. Mivel 0 P(AB)
P(AB) P(A) és 0
P(A) és 0 P(AB)
P(AB) P(B), így P2(AB)
P(B), így P2(AB) P(A).P(B). Ezért
P(AB)-P(A).P(B)
P(A).P(B). Ezért
P(AB)-P(A).P(B) P(AB)-P2(AB)=P(AB)(1-P(AB))
P(AB)-P2(AB)=P(AB)(1-P(AB))
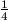 ,
hiszen ismert, hogy ha 0
,
hiszen ismert, hogy ha 0 x
x 1, akkor
x.(1-x)
1, akkor
x.(1-x)
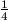 .
.
II. Most belátjuk, hogy
P(AB)-P(A)P(B)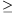 -
-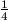 .
.
a) Ha P(A)+P(B) 1.
1.
Mivel P(AB)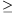 0, ezért
P(A)P(B)-P(AB)
0, ezért
P(A)P(B)-P(AB) P(A)P(B)
P(A)P(B)
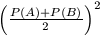

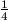 a
számtani és mértani közép közötti összefüggést felhasználva.
a
számtani és mértani közép közötti összefüggést felhasználva.
b) Ha P(A)+P(B)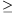 1, akkor könnyen bizonyítható, hogy
P(AB) legalább P(A)+P(B)-1
lesz. Így P(A)P(B)-P(AB)
1, akkor könnyen bizonyítható, hogy
P(AB) legalább P(A)+P(B)-1
lesz. Így P(A)P(B)-P(AB) P(A)P(B)-P(A)-P(B)+1=(1-P(A))(1-P(B))
P(A)P(B)-P(A)-P(B)+1=(1-P(A))(1-P(B)) P(B)(1-P(B))
P(B)(1-P(B))
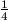 .
.
B. 3371. Legfeljebb hány közös érintője lehet két ellipszisnek, ha közös az egyik fókuszuk? (5 pont)
Megoldásvázlat. A két ellipszisnek legfeljebb két közös érintője lehet.
Ismert, hogy ha egy ellipszis egyik fókuszát tükrözzük az ellipszis tetszőleges érintőjére, akkor a másik fókusz köré írt vezérkör egy pontját kapjuk. Ezért a két ellipszis közös fókuszának a közös érintőre való tükörképe mindkét ellipszisnek a másik fókusza köré írt vezérkörén rajta van. a két vezérkörnek viszont legfeljebb két közös pontja van, ezért az ellipsziseknek sem lehet több közös érintőjük.

