Matematikából kitűzött gyakorlatok és feladatok
2000. április

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 580. Kati dolgozatot írt matematikából, majd még egy javító dolgozatot is írt. A tanár a két jegy helyett azok átlagát írta be az osztályozó füzetébe. Bizonyítsuk be, hogy Kati akkor jár jobban ezzel, ha a többi matematika jegyeinek átlaga nagyobb a két dolgozatjegy átlagánál.

Kovács Gabriella, Budapest

C. 581. Négy jármű egyszerre indul el A-ból, és egymást követően egyenlő időközönként érkezik meg B-be. A leggyorsabb és a leglassúbb jármű sebessége v₁, ill. v₄. Mekkora a másik két jármű sebessége?

C. 582.  Az ábrán látható sáv szélessége 1 m. Mekkora a területe?

Nagy Zoltán 9. o.t., Budapest

C. 583.  Egy gúla alapja egység oldalú négyzet. Egyik oldaléle szintén egységnyi hosszú és egybeesik a gúla magasságával. Mekkora a legnagyobb lapszöge?

Salát Máté 9. o.t., Budapest

C. 584. Egy körnek a területét vagy a kerületét tudjuk jobban (kisebb relatív hibával) közelíteni a körbe írt szabályos n-szög segítségével?

A B pontversenyben kitűzött feladatok

B. 3362. Tizennyolc gyerek megoldotta a KöMaL áprilisi számának egy-egy feladatát. A megoldásokat elektronikus levelezéssel (e-mailen keresztül) akarják megbeszélni. Legalább hány e-mailt kell küldeniük egymásnak, hogy mindegyikük megtudja mindegyik megoldást? (Minden e-mail annyiszor számít, ahány embernek küldik.) (5 pont)

Gyanta Nándor ötletéből

B. 3363. Van-e olyan háromszög, amit két vágással három egybevágó részre lehet darabolni? (3 pont)

B. 3364. Tegyük fel, hogy 15 különböző (pozitív) prímszám számtani sorozatot alkot. Igazoljuk, hogy a sorozat két szomszédos tagjának a különbsége 30000-nél nagyobb. (3 pont)

Székelyhidi Tamás 11. o.t., Budapest

B. 3365. Bizonyítsuk be, hogy ha abc=1 és 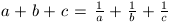, akkor az a, b, c számok közül legalább az egyik 1-gyel egyenlő. (3 pont)

Gyanta Nándor, Budapest

B. 3366. Ismét útnak indul az F. 3279. feladat szöcskéje. Most egy r sugarú kör és egy, a kör középpontján át nem menő egyenes pontjai között ugrál, a körről az egyenesre, onnan pedig vissza a körre. Bizonyítsuk be, hogy r hosszúságú ugrásokkal legfeljebb 8 pontba juthat el. (5 pont)

Hraskó András, Budapest

B. 3367. Egy egyenlő szárú háromszög alakú papírlapot összehajtottunk úgy, hogy az alap A csúcsa a BC szár felezőpontjába került. Ekkor a hajtás élének egyik végpontja az AC szárat p:q arányban osztja. Milyen arányban osztja a hajtás élének másik végpontja az AB alapot? (5 pont)

A Magyar Hírlap nyomán

B. 3368. Hány megoldása van a pozitív egész számok körében az x⁷+y⁸=z⁹ egyenletnek? (4 pont)

Behm Andrea, Nagykanizsa

B. 3369. Egy tetraéder mindegyik élén kijelöljük az egyik harmadolópontot. Mekkora lehet az ezek által meghatározott konvex test és a tetraéder térfogatának hányadosa? (4 pont)

B. 3370. A és B két véletlen esemény. Igazoljuk, hogy

|P(A^.B)-P(A)^.P(B)|1/4.

(5 pont)

B. 3371. Legfeljebb hány közös érintője lehet két ellipszisnek, ha közös az egyik fókuszuk? (5 pont)

A pontversenyben kitűzött nehezebb feladatok

A. 227. Létezik-e olyan pozitív egész n, hogy tetszőleges nem 0 i számjegy esetén az n, 2n, 3n, ..., 2000n számok mindegyikének tízes számrendszerbeli alakjában ugyanannyiszor fordul elő az i?

A. 236. Egy háromszög területe t, oldalai a<b<c, a hozzájuk tartozó súlyvonalak hossza rendre s_a, s_b, s_c. Bizonyítsuk be, hogy

4acs_as_c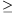16t²+(b²-a²)(c²-b²).

A. 237. Egy konvex n-szögnek megrajzoltuk kn+1 különböző átlóját (n és k pozitív egészek). Igazoljuk, hogy a megrajzolt átlók közül kiválasztható 2k+1 olyan, amelyek egy töröttvonalat alkotnak, és közülük semelyik kettő nem metszi egymást.

A. 238. Legyen x pozitív valós szám és k pozitív egész. Bizonyítsuk be, hogy ha x^k+1/x^k és x^k+1+1/x^k+1 racionális, akkor x+1/x is racionális.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. április 15.