New exercises and problems in Mathematics
May 2000
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in May 2000 |
C. 585. In certain audio cassettes, a 0.0075 mm wide tape is wound on the reels whose common diameter is 11 mm. The centres of the reels are in distance 42 mm apart. How long a tape can a usable cassette (in which the tape can be wound up on each reel without getting stuck at any point) contain?
C. 586. Find the maximum possible number of sides of a convex polygon which does not have two consecutive obtuse angles.
C. 587. Let n denote a positive integer. Connect the point of the x-axis whose abscissa is n with the points of the y-axis whose ordinates are n-1 and n+1, respectively. Connect, moreover, the point of the y-axis whose ordinate is n with the points of the x-axis whose abscissas are n-1 and n+1, respectively. Determine the area enclosed by the four segments obtained this way.
C. 588. Determine the inverse of the function
f:(- ,-2)
,-2)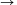 R, x
R, x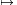 2x2+8x+7.
2x2+8x+7.
C. 589. A straight stick got stuck in a drainage ditch of a V-shaped cross-section. The two ends of the stick lean against the two sides of the ditch, forming equal angles with both sides. Prove that the two ends of the stick rest in the same distance from the bottom of the ditch.
 |
New problems in May 2000 |
B. 3372. In a certain right-angled triangle, the medians can be arranged to form the sides of another right-angled triangle. Prove that the two triangles are similar. (3 points)
Proposed by: N. Gyanta, Budapest
B. 3373. Lines e and g, respectively, are drawn on each side of a given line f, in a unit distance from f. Points E,G and F lie on the corresponding lines such that triangle EFG has a right angle at vertex F. Determine the length of the altitude of the triangle starting at F. (3 points)
Proposed by: Gy. Pap, Debrecen
B. 3374. A certain exam consists of a written and an oral part; the students can obtain an integer mark between 0 and 9 at each part. In the final evaluation student A is ranked higher than B if A's mark is not worse than that of B at each part of the exam, and is strictly better than that of B at one of the exams at least. In a group of 20 students no two students obtained identical results. Prove that there are three students A,B,C in the group such that A is ranked higher than B and B is ranked higher than C. (4 points)
B. 3375. Is there any polynomial
p(x)=x2+ax+b whose integers coefficients
satisfy a2-4b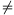 0 and which assigns a perfect square
value to at least 2000 different integers? (4 points)
0 and which assigns a perfect square
value to at least 2000 different integers? (4 points)
B. 3376. In a triangle ABC, side AC is of unit length. The median starting at vertex A divides the angle at A in the ratio 1:2. How long may side AB be? (3 points)
S. Mihalovics, Esztergom
B. 3377. Let k denote an odd integer. Find the remainder when the sum 2n-1k2+2n-2k4+2n-3k8+...+2k2n-1+k2n is divided by 2n+2. (4 points)
Proposed by: M. Bencze, Brassó
B. 3378. The pupils of a graduating class apply at five different universities; each university receiving the application of at least half of the pupils. Prove that there exist two universities such that at least one fifth of the pupils apply at both institutions. (5 points)
B. 3379. In a triangle ABC, the angle
bisectors AA1,
BB1, CC1 meet at point O. Prove that 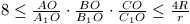 , where R and r,
respectively, denote the radii of the circumscribed and the inscribed
circle. (5 points)
, where R and r,
respectively, denote the radii of the circumscribed and the inscribed
circle. (5 points)
Proposed by: M. Bencze, Brassó
B. 3380. Show that every parallelepiped has a vertex where either none of the 3 plane angles between the edges are acute or none of the 3 dihedral angles are obtuse. (4 points)
B. 3381. A teacher noticed that among the 30
pupils who attend to her class, two celebrate their birthdays on the
very same day. This is not a big surprise: prove that the probability
of two people out of 30 having the same birthday is at least 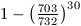 . (5 points)
. (5 points)
 |
New advanced problems in May 2000 |
A. 239. Construct a triangle, if the three points where the extensions of the medians intersect the circumcircle of the triangle are given.
Proposed by: J. Rácz, Budapest
A. 240. Let n and m denote positive integers. Prove that

where 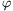 is Euler's totient function.
is Euler's totient function.
A. 241. Prove that, for every positive integer n,
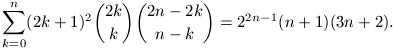
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: megoldas@komal.elte.hu.
