New exercises and problems in Mathematics
September 2000
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in September 2000 |
C. 590. According to the law of gravity, an object falling free to the earth's surface moves through s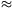
4.903t2 meters in t seconds. How is this formula modified if distance is measured in feet and time is measured in minutes?
C. 591. Ann thought of 5 numbers and told Bob the list of all the sums that can be obtained by adding any two of the numbers. This list goes as follows: 6,7,8,8,9,9,10,10,11,12. Help Bob to find out which numbers Ann was thinking of.
C. 592. Determine the average of all 5-digit palindromes. (A palindrome like 12421 is a number, reading the same backward as forward.)
C. 593. Peter selected a few stamps from his collection; one of each of the face values: 1,2,..., 37 forints. His plan is to arrange them in groups such that the sum of the face values is the same in each group. How many different arrangements can be made?
C. 594. In a cyclic trapezium, a and d denote the length of one base and the sum of the lengths of the other three sides. Given a and d, determine the sides of the trapezium which has a maximal area.
 |
New problems in September 2000 |
B. 3382. The sum of the squares of 17 different positive prime numbers is again a perfect square. Prove that the difference between the squares of the two largest numbers is divisible by the smallest one. (3 points)
Proposed by: A. Gyurcsek, Veszprém
B. 3383. In a right angled triangle, sa and sb denote the medians that belong to the legs of the triangle, the median belonging to the hypotenuse is sc. Determine the maximum value of the expression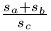 
. (3 points)
Proposed by: Á. Besenyei, Tatabánya
B. 3384. Prove that if a, b, c>0, then
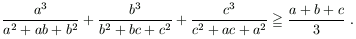(3 points)
Proposed by: M. Ábrány, Beregszász
B. 3385. The sides of a triangle ABC satisfy BC=AC+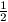
AB. Point P divides side AB in the ratio 3:1. Prove that 
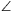PAC=2(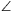CPA). (4 points)
B. 3386. 2001 points are given in a 5x5x10 rectangular box. Prove that there are two of them whose distance is not greater than
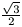. (4 points)
Proposed by: M. Ábrány, Beregszász
B. 3387. Determine the angle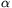 
if, for some nonzero vector p, the sum of p and the vector obtained from p by rotating it by 2 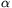equals to the vector obtained from p by rotating it by 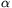. (3 points)
B. 3388. In a triangle ABC, the angle at vertex B measures 120o. The bisector of this angle intersects side AC at point P. The bisector of the exterior angle at vertex C intersects line AB at Q, and finally, segment PQ intersects side BC at R. Find the measure of 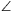PRA. (5 points)
Proposed by: S. Katz, Bonyhád
B. 3389. Define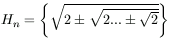 
,
where each surd contains n square root signs. How many different real numbers belong to the set 
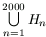? (4 points)
B. 3390. In a certain tetrahedron, each vertex is incident to three edges of length 5,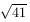 
and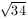 
, respectively. Determine the length of each segment between the midpoints of some two opposite edges of the tetrahedron. (5 points)
B. 3391. When Bob, holding his valid reserved ticket, entered the railway carriage, he found, to his utmost surprise, that all the 78 seats had already been occupied. In fact, Dan entered the carriage without a reservation, and the other 77 passengers, including Jim, though having a valid reservation, not necessarily sat on the seats they had booked. Bob immediately asked the passenger occupying his seat to find another seat for himself. Next, the passenger who had to stand up went to his own reserved seat, and so on until Dan got exposed. What is the probability that Jim could remain seated all along? (5 points)
 |
New advanced problems in September 2000 |
A. 242. 2001 points are given in a 5x5x10 rectangular box. Prove that there can be found two points among them whose distance is less than 0.7.
A. 243. Determine all pairs of prime numbers p,q which satisfy
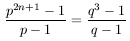for some integer n>1.
Proposed by: E. Fried, Budapest
A. 244. A sequence of numbers is called of Fibonacci-type if each term, after the first two, is the sum of the previous two. Prove that the set of positive integers can be partitioned into the disjoint union of infinite Fibonacci-type sequences.
Proposed by: B. Énekes, Tolna
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.