New exercises and problems in Mathematics
October 2000
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in October 2000 |
C. 595. Find all 3-digit numbers which are equal to the sum of the factorials of their respective digits.
C. 596.
Solve the equation
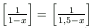on the set of real numbers. ([a] denotes the integer part of a, that is, the largest integer not exceeding a.)
C. 597.
Prove that, in any right triangle, the distance between the incentre and the
circumcentre is at least
(
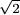-1) times the radius of the circumcircle.
C. 598. Is it possible to find 2000 positive integers such that none of them is divisible by any of the other numbers but the square of each is divisible by all the others?
Proposed by: M. Ábrány, Ukraine
C. 599. A right cone of unit height whose circular base has a radius R is truncated in the following way. First, it is cut along a plane whose distance from the base is h. Next, the removed cone is reflected in the cutting plane and its image is removed from the frustum. Calculate the volume of the solid obtained this way.
 |
New problems in Oktober 2000 |
B. 3392. We have 25 vessels whose volumes are 1,2,..., 25 litres, respectively. 10 vessels are to be selected such that from an unlimited supply of water, exactly 1 litre can be measured with the help of any two selected vessels. How many different selections can be made? (4 points)
Proposed by: L. Kozma, Székelyudvarhely
B. 3393. Triangles ABC and A'B'C' are given in the plane such that points A', B' and C' are the midpoints of segments CC', AA' and BB', respectively. Determine the ratio of the areas of the two triangles. (3 points)
B. 3394. Prove that the positive numbers a, b, c are the lengths of the sides of some triangle if and only if (a2+b2+c2)2>2(a4+b4+c4). (3 points)
B. 3395. Construct the pentagon A1A2A3A4A5, given the reflections of point Ai through point Ai+1 for i=1, 2, ..., 5, respectively, where A6=A1. (3 points)
B. 3396. Find all positive integer solutions of the equation xy+yz+zx-xyz=2. (4 points)
B. 3397. An acute triangle ABC and a rectangle KLMN are given such that N is incident to segment AC and K,L are incident to segment AB. Translating the rectangle parallel to AC an other rectangle K'L'M'N' is obtained whose vertex M' is incident to segment BC. Prove that the line connecting the intersection point of CL' and AB with the intersection point of AM and CB is perpendicular to line AB. (4 points)
B. 3398. Points A, B, C, D are points in the space such that segments AB and CD are of 4 unit length while segments BC and DA are of 5 unit length. Let x and y denote the squares of the lengths of segments AC and BD, respectively. Plot in the Cartesian system all pairs (x,y ) that arise this way. (4 points)
Proposed by: A. Hraskó Budapest
B. 3399. Two circles e and f are given in the plane, and a point P outside the circles. A tangent line from P is drawn to each circle, touching the circles at points E and F, respectively. Prove that the ratio of the lengths of the two segments that the two circles cut out of line EF does not depend on the choice of the two tangent lines.(5 points)
B. 3400.
For a given interger d let Sd={x
2+dy2:x,y
Z}.
Assume are a
Sd, b
Sd such that b is a prime and
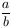is an integer. Prove that
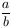
Sd. (5 points)
Proposed by: M. Csörnyei, London
B. 3401. In a ware house there are a lot of parcels, each weighing at most 1 (metric) ton. We have two lorries which can be loaded with weights of 3 and 4 tons, respectively. A contract is to be made according to which we carry at least N tons of wares at each turn. What is the largest value of N with which we may undertake the contract? (5 points)
 |
New advanced problems in October 2000 |
A. 245. We want to make a round trip with our car. There are a few gas-stations along the road where the total amount of fuel is enough to make two round trips. Prove that there is a station from where the round trip can be completed in both directions.
A. 246. Find all quadruples of real numbers x, y, z, w which satisfy x+y+z+w=x7+y7+z7+w7=0.
Shay Gueron, Haifa
A. 247. Prove that there is no point on the lines determined by the sides of the unit square whose distance from each vertex of the square is rational.
Á. Kovács, Budapest
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.