A 2000 novemberi A-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 248. Hányféleképpen lehet egy n-elemű halmaz hatványhalmazát két diszjunkt részre: az I és H halmazokra bontani úgy, hogy a következő feltételek egyszerre teljesüljenek?
a) tetszőleges a, b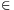 I esetén
a
I esetén
a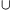 b
b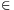 I és
a
I és
a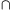 b
b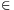 I;
I;
b) tetszőleges a, b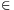 H esetén
a
H esetén
a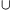 b
b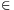 H és
a
H és
a b
b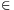 H;
H;
c) tetszőleges a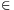 I, b
I, b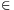 H esetén a
H esetén a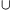 b
b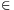 I és a
I és a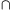 b
b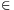 H.
H.
(Egy halmaz hatványhalmazának az összes részhalmazainak halmazát nevezzük.)
Javasolta: Csirmaz Előd, Budapest
Megoldás. Jelöljük az n-elemű halmazt S-sel, elemei legyenek x1, ..., xn.
Könnyen ellenőrizhető, hogy megfelelő az a két felbontás, amikor az összes részhalmaz H-ba, illetve I-be kerül, azaz H és I valamelyike üres. Nevezzük ezeket triviális felbontásoknak. A továbbiakban pontosan leírjuk, mik a nemtriviális felbontások, amelyekben sem H, sem I nem üres.
Először megmutatjuk, hogy egy nem triviális felbontásban 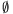
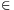 H és
S
H és
S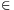 I. Legyen ugyanis h
I. Legyen ugyanis h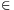 H és i
H és i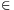 I két
tetszőleges halmaz; ekkor
I két
tetszőleges halmaz; ekkor 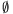 =
=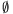
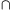 h
h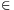 H és S=S
H és S=S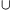 i
i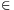 I az a), b) és c)
tulajdonságok miatt.
I az a), b) és c)
tulajdonságok miatt.
Tegyük fel, hogy n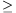 1, és
tekintsük most az {x1}, \dots, {xn} egyelemű részhalmazokat. Azt állítjuk, hogy ezek
közül pontosan egy tartozik I-be. Ha mindegik egyelemű halmaz
H-ba tartozna, akkor a c) tulajdonság miatt az {x1}
1, és
tekintsük most az {x1}, \dots, {xn} egyelemű részhalmazokat. Azt állítjuk, hogy ezek
közül pontosan egy tartozik I-be. Ha mindegik egyelemű halmaz
H-ba tartozna, akkor a c) tulajdonság miatt az {x1}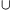 {x2}
{x2}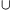 ...
...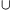 {xn}=S halmaz is
H-nak lenne eleme, ami ellentmodás. Az egyelemű részhalmazok között
tehát van olyan, ami I-be tartozik. Ha az egyelemű halmazok közül
legalább kettő tartozna I-be, akkor az a) tulajdonság miatt ezek
metszete,
{xn}=S halmaz is
H-nak lenne eleme, ami ellentmodás. Az egyelemű részhalmazok között
tehát van olyan, ami I-be tartozik. Ha az egyelemű halmazok közül
legalább kettő tartozna I-be, akkor az a) tulajdonság miatt ezek
metszete, 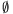 is I-beli lenne, ami
szintén ellentmondás.
is I-beli lenne, ami
szintén ellentmondás.
Legyen {xj} az az
egyelemű halmaz, amely I-be tartozik. Az a) és b) tulajdonságok alapján
megállapíthatjuk, hogy minden olyan r részhalmaz I-bve tartozik,
amelynek {xj} része; más szóval, ha
xj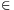 r, akkor r
r, akkor r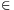 I. Megfordítva, ha egy r részhalmaznak
xj nem eleme, akkor r
I. Megfordítva, ha egy r részhalmaznak
xj nem eleme, akkor r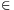 I nem lehetséges, ugyanis r
I nem lehetséges, ugyanis r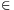 I esetén az a) tulajdonság alapján r
I esetén az a) tulajdonság alapján r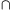 {xj}=
{xj}=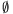 is I-beli lenne. Azt kaptuk tehát,
hogy egy r halmaz akkor és csak akkor tartozik I-be, ha
xj-t tartalmazza.
is I-beli lenne. Azt kaptuk tehát,
hogy egy r halmaz akkor és csak akkor tartozik I-be, ha
xj-t tartalmazza.
A nemtriviális felbontások száma tehát a lehetséges xj-k száma, azaz n.
Az n=0, azaz S=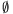 esetben a két triviális felbontás ugyanaz:
I=H=
esetben a két triviális felbontás ugyanaz:
I=H=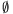 és más felbontás
nincs; az összes felbontások száma tehát 1. Ha n
és más felbontás
nincs; az összes felbontások száma tehát 1. Ha n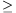 1, akkor a két triviális felbontás különböző, az összes
felbontások száma n+2.
1, akkor a két triviális felbontás különböző, az összes
felbontások száma n+2.
A. 249. Legyenek a, b, c, t pozitív számok és abc=1. Igazoljuk, hogy
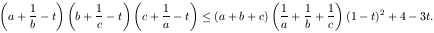
Megoldás. A 2000. évi Nemzetközi Matematikai Diákolimpia 2. feladatában azt kellett bizonyítani, hogy ha az a,b,c pozitív számok szorzata 1, akkor
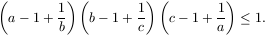
A részletes megoldás megtalálható a KöMaL 2000/7. számának 387. oldalán. Ezt az egyenlőtlenséget fel fogjuk használni.
Mint egy kis számolással ellenőrizhető, az egyenlet az abc=1 azonosság többszöri felhasználásával átrendezhető a következő alakba:
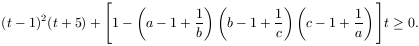
A baloldalon álló összegnek mindkét tagja nemnegatív.
A. 250. Tekintsük a Hanoi tornyai néven közismert játék négytornyos változatát: n darab különböző méretű korong egymásra van helyezve nagyság szerint sorban úgy, hogy alul van a legnagyobb, felül a legkisebb. A korongokat egy másik helyre kell áthelyezni a következő szabályok betartásával:
Bizonyítsuk be, hogy a szükséges minimális lépésszám legalább 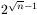 és kisebb, mint
és kisebb, mint 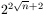 .
.
Énekes Béla (Tolna) ötletéből
Megoldás.A megoldáshoz többször is fel fogjuk használni azt az ismert tényt, hogy három torony esetén a minimális lépésszám pontosan 2n-1.
Először is megmutatjuk, hogy az f függvény szigorúan monoton növekvő. Legyen n<m, és tekintsünk egy pakolási sorrendet, amely m korongot f(m) lépésben át tud pakolni. Hajtsuk végre ugyanezt a pakolási sorrendet úgy, hogy csak a legkisebb n korong mozgatásait hajtjuk végre. Ezáltal az n kisebb korongot pakoltuk át, kevesebb mint f(m) lépésben.
A felső becsléshez bebizonyítjuk, hogy f(k2)<22k. Ebből a becslés következik, mert a
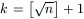 választással
n<k2 és
választással
n<k2 és 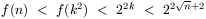 . Állításunk igazolásához megadunk egy
konstrukciót, amelyben k2
korong kevesebb, mint 22k
lépésben áthelyezhető. Jelöljük A,B,C,D-vel a négy helyet,
ahova a korongokat pakolhatjuk, és tegyük fel, hogy mondjuk az
A helyről kell az összes korongot a B helyre
átpakolnunk. Osszuk fel a korongokat k-as csoportokra. Ha
egyszerre egy egész k-as csoportokat mozgathatnánk az
A,B,C helyek között, akkor 2k-1 lépés elegendő lenne. Egy egész
k-as csoportot viszont bármelyikről bármelyikre átpakolhatunk
2k-1 lépésben a D
felhasználásával. Ez összesen (2k-1).(2k-1)<22k lépés. (Az ábra a k=3 esetre
mutatja be az algoritmust.)
. Állításunk igazolásához megadunk egy
konstrukciót, amelyben k2
korong kevesebb, mint 22k
lépésben áthelyezhető. Jelöljük A,B,C,D-vel a négy helyet,
ahova a korongokat pakolhatjuk, és tegyük fel, hogy mondjuk az
A helyről kell az összes korongot a B helyre
átpakolnunk. Osszuk fel a korongokat k-as csoportokra. Ha
egyszerre egy egész k-as csoportokat mozgathatnánk az
A,B,C helyek között, akkor 2k-1 lépés elegendő lenne. Egy egész
k-as csoportot viszont bármelyikről bármelyikre átpakolhatunk
2k-1 lépésben a D
felhasználásával. Ez összesen (2k-1).(2k-1)<22k lépés. (Az ábra a k=3 esetre
mutatja be az algoritmust.)
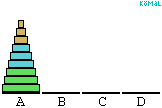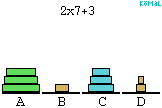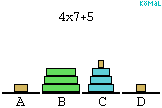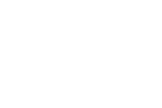
Az alsó becsléshez a követekző állításokat bizonyítjuk be:
I. Három torony esetén, tetszőleges helyzetből kiindulva, legalább 2n-2+1 lépés szükséges ahhoz, hogy az összes korongot legalább egyszer elmozdítsuk.
II. Négy torony esetén, tetszőleges helyzetből kiindulva, legalább
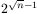 lépés szükséges ahhoz, hogy az
összes korongot legalább egyszer elmozdítsuk.
lépés szükséges ahhoz, hogy az
összes korongot legalább egyszer elmozdítsuk.
A második állításból a feladat alsó becslése triviálisan következik.
Az I. állítás bizonyítása. Legyen a két legnagyobb korong A, illetve B. Amikor A-t vagy B-t mozgatjuk, az összes kisebb korongnak egy tornyot kell alkotnia. Tekintsük A-nak és B-nek egy-egy olyan mozgatását, amelyek között csak a kisebb korongokat mozgatjuk; könnyű végiggondolni, hogy a kisebb korongok a két áthelyezéskor nem ugyanazt a tornyot alkotják. A kisebb korongokat ezért összesen legalább 2n-2-1 lépésben átmozgatjuk az egyik helyről a másikra. Ez, A és B egy-egy áthelyezésével együtt, legalább 2n-2+1 lépés. Ezzel az I. állítást igazoltuk.
A II. állítás bizonyítása. Az állítást teljes indukcióval
igazoljuk. Mivel az n korong elmozdításához mindenképpen
szükséges n lépés, és n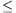 39 esetén
39 esetén 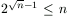 ,
az állítás n
,
az állítás n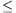 39-re
triviális. Legyen tehát n
39-re
triviális. Legyen tehát n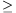 40, és tegyük fel, hogy az állítás minden kisebb
értékre igaz.
40, és tegyük fel, hogy az állítás minden kisebb
értékre igaz.
Legyen 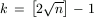 , és tegyük fel, hogy
egy f(n) hosszú lépéssorozat során minden korongot
elmozdítottunk. A lépéssorozatot két részre osztjuk. A sorozat első
fele annyi lépésből áll, amelyben pontosan n-k korongot
mozdítunk el. A sorozat második fele az összes többi lépésből áll.
, és tegyük fel, hogy
egy f(n) hosszú lépéssorozat során minden korongot
elmozdítottunk. A lépéssorozatot két részre osztjuk. A sorozat első
fele annyi lépésből áll, amelyben pontosan n-k korongot
mozdítunk el. A sorozat második fele az összes többi lépésből áll.
Ha a sorozat második felében is legalább n-k korongot elmozdítunk, akkor mindkét fél sorozat legalább f(n-k) lépésből áll, vagyis a lépések száma legalább
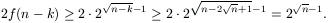
Az állítás tehát ebben az esetben igaz.
Vizsgáljuk most azt az esetet, ha a lépéssorozat második felében (n-k)-nál kevesebb korongot mozdítunk el. Színezzük pirosra azokat a korongokat, amiket a lépéssortozat első felében nem mozdítunk el; ezek száma k. Színezzük kékre azokat a korongokat, amiket a lépések második felében nem mozdítunk el; ezek száma legalább k+1. Mivel minden korongot legalább egyszer elmozdítunk, a piros és a kék korongok halmaza diszjunkt.
Legyen C a legkisebb kiszínezett korong. Ha C színe kék, akkor a lépéssorozat második felében C nem mozdul el. A C korongra nem helyezhetjük rá a nála nagyobb piros korongokat; a k darab piros korongot a lépéssorozat második felében úgy mozdítjuk el, hogy csupán három torony között mozoghatnak. Ezért a piros korongok elmozdításához legalább 2k-2+1 lépésre van szükség.
Hasonlóan, ha a C korong piros, akkor a sorozat első felében a legalább k+1 darab kék korong csupán három torony között mozoghat, ezért elmozdításukhoz legalább 2k-1+1 lépés szükséges. A lépésszám mindkét esetben legalább
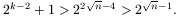
Megjegyzések. 1. Az alsó becslésre adott bizonyításban Csóka Endre dolgozatának ötleteit használtuk fel.
2. Jobb felső becslést kaphatunk, ha a korongokat nem egyenlő méretű csoportokra osztjuk. Ha például a csoportok mérete felülről lefelé 1,2,...,k, akkor a kapott becslés:

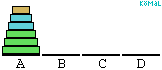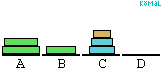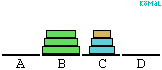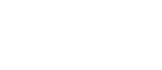
Ebből következik például, hogy 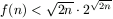 .
.
3. Az alsó becslés lépéseinek kis módosításával könnyű
bebizonyítani, hogy 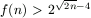 . (Csupán
k-t kell máshogy megválasztani:
. (Csupán
k-t kell máshogy megválasztani: 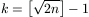 .) Ez az eredmény az előbbi becsléssel együtt adja,
hogy
.) Ez az eredmény az előbbi becsléssel együtt adja,
hogy
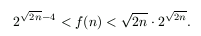
4. Be lehet bizonyítani, hogy a 2. megjegyzésben leírt becslés éles; tetszőleges pozitív egész k esetén
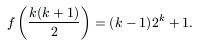
A többtornyos Hanoi-tornyokról bővebben például az American Mathematical Monthly 1941. márciusi számának 216-219. oldalán olvashatunk.

