Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A 2000. decemberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

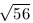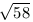B. 3412. Mutassuk meg, hogy két kivétellel minden pozitív egész q számhoz létezik olyan p egész, hogy <p/q<. (3 pont)

Az NRICH Online Maths Club feladata

Megoldás.Az átrendezéssel kapható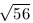 q<p<q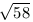 követelményt biztosan kielégíti legalább egy p egész, ha q (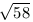-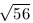)> 1, azaz q>1/(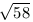-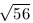)=(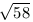+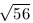)/2, azaz, ha q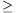8. A fennmaradó esetekre közvetlen számolással adódik, hogy 7<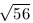< <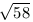8 és 22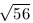<3<3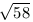 <23 miatt q=1 és q=3 értékére nincs megfelelő p, másrészt q=2,4,5,6,7-re p=15,30,38,45,53 megfelelőek.

B. 3413. A tavaly még professzionálisnak nevezett magyar labdarúgó bajnokság egy csoportjában az idén 8 csapat szerepel. Minden meccs egyik résztvevője otthon, a másik idegenben játszik. Egy idényben, amikor minden csapat minden másikkal pontosan egyszer játszik, egy csapat sorsolását igazságosnak nevezzük, ha felváltva játszik otthon és idegenben. Lehet-e olyan sorsolást készíteni, amelyben mind a 8 csapat sorsolása igazságos? (4 pont)

Megoldás.Minden csapathoz rendeljünk hozzá egy 7 hosszú 0-1 sorozatot, ahol 0 azt jelenti, hogy az adott fordulóban a csapat idegenben, 1 pedig azt, hogy otthon játszott. Ha egy csapat sorsolása igazságos, akkor a hozzá rendelt sorozat vagy 0101010, vagy 1010101.
Ha tehát kiválasztunk tetszőleges három csapatot, akkor ha mindhármuk sorsolása igazságos lenne, akkor közülük legalább kettőhöz ugyanaz a sorozat lenne rendelve. Ez viszont nem lehet, mert az egymás elleni meccsüket valamelyikük otthon, a másik pedig idegenben játssza.
Tehát már 3 csapat esetén sem lehet igazságos sorsolást készíteni.

B. 3414. Egy húrnégyszög átlói merőlegesek egymásra, oldalhosszai négyzetének összege 8 egység. Határozzuk meg a körülírt körének sugarát. (3 pont)

Javasolta: Besenyei Ádám, Tatabánya

Megoldás.

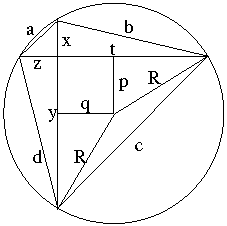
Az ábra jelöléseit használva: 8=a2+b2+c2+d2=2(x2+y2+z2+t2)=((y+x)2+(y-x)2+(t+z)2+(t-z)2)=4((R2-q2)+p2+(R2-p2)+q2)=8R2, tehát a körülírt kör sugara egységnyi.

B. 3415. A p paraméter mely értékeire van az

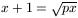
egyenletnek pontosan egy valós gyöke? (4 pont)

Megoldás.A p=0 megfelel (x=-1 az egyetlen megoldás).

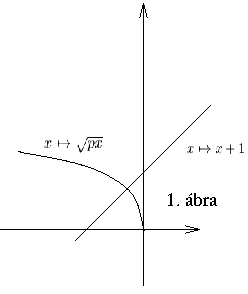
Ha p<0, akkor az 1. ábráról leolvasható, hogy az x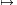x+1 és az 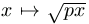függvények grafikonja egyetlen pontban találkozik. Ha p>0, akkor a feltétel azt jelenti, hogy az y=x+1 egyenes az 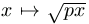függvény görbéjének érintője. (2. ábra).

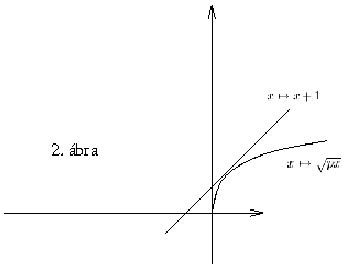
Ekkor az x+1=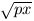 egyenletnek csak egy megoldása van. Tehát D=(2-p)2-4=0, azaz p=0 vagy p=4. Csak ez utóbbi teljesíti a p>0 feltételt. Tehát a feladat kérdésére a válasz: p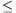0 és p=4.

B. 3416. Egy négyszöglapokkal határolt konvex poliéder felszíne A, éleinek négyzetösszege Q. Bizonyítsuk be, hogy Q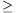2A. (4 pont)

Javasolta: Besenyei Ádám, Tatabánya

Megoldás.Minden él két lapot határol. Így a feladat állítása következik abból, hogy egy négyszög területe legfeljebb akkora, mint az oldalai négyzetösszegének a negyede. Az ábra jelöléseivel a terület kétszerese:

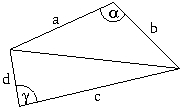
2T=absin 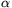+cdsin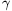 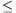ab+cd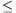(a2+b2)/ 2+(c2+d2)/ 2=(a2+b2+c2+d2)/ 2, tehát

2A=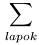2T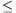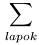(a2+b2+c2+d2)/ 2=Q.

B. 3417. Tekintsük a síkon az összes olyan kört, amelynek egyenlete felírható

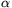 ((x-2)2+y2-1)+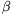((x+2)2+y2-1)=0

alakban, ahol 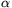és 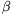valós számok. Hol vannak azok a pontok, amelyek egyik ilyen körön sincsenek rajta? (4 pont)

Megoldás.Írjuk át az egyenletet

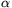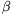(+)(x2+y2+3)+4(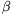-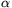)x=0    (1)

alakba.

Egy (a,b) pont pontosan akkor van rajta az ezzel az egyenlettel meghatározott alakzaton, ha

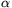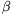(+)(a2+b2+3)+4(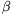-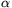)a=0.    (2)

Ha a=0, akkor ez csak akkor teljesülhet, ha 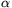+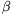=0. Ekkor viszont (1) nem kör egyenlete. Tehát az x=0 egyenes pontjai egyik körön sincsenek rajta.

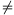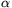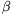
A továbbiakban tegyük fel, hogy a 0. Ha + 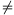0, akkor feltehető, hogy 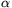+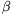=1. Az (1) egyenlet ekkor így írható:

(x+2(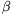-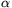))2+y2=4(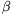-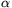)2-3.

Ez pontosan akkor kör egyenlete, ha a jobb oldali kifejezés pozitív. A (2) egyenletből kapjuk, hogy 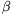-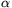=(a2+b2+3)/(-4a). Ezért

4(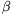-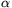)2-3= [(a2-3)2+b4+2a2b2+6b2]/4a2.

Ez csak akkor nempozitív, ha a2=3 és b=0. Tehát a (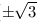;0) pontok kivételével mindig találunk megfelelő kört.

Vagyis azok a pontok amelyek egyik körön sincsenek rajta vagy az y tengelyen vannak, vagy pedig a (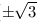;0) pontok.

B. 3418. Az ABC háromszögben az A, B, illetve C csúcsokból induló súlyvonalak a háromszög köré írt kört rendre az A1, B1, illetve C1 pontokban metszik. Bizonyítsuk be, hogy tA1BC+tB1CA+tC1AB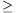tABC. (5 pont)

Javasolta: Varga István, Békéscsaba

Megoldás.Ismert, hogy a háromszög magasságpontját az oldalegyenesekre ill. az oldalfelező pontokra tükrözve a körülírt kör egy-egy pontjához jutunk. Ezek után tekintsük az ábrát.

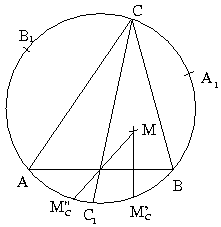
MC''MC' AB, valamint C1 az M pont két tükörképe közé esik. Így tAMB=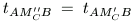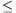tAC1B. Hasonlóan tBMC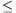tBA1C és tCMA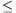tCB1A. A három egyenlőtlenséget összegezve kapjuk, hogy tABC=tAMB+tBMC+tCMA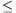tAC1B+tBA1C+tCB1A. Ezzel az állítást beláttuk.

B. 3419. A sík mely pontjaiból húzható az y=x3 egyenletű görbéhez három érintő? (4 pont)

Megoldás.Két érintő

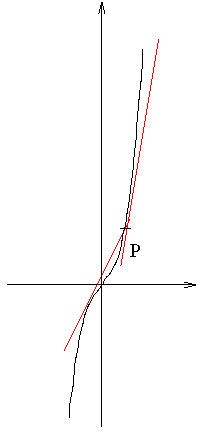
Két (másfél) érintő

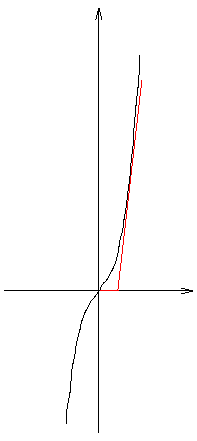
Egy érintő

Három érintő

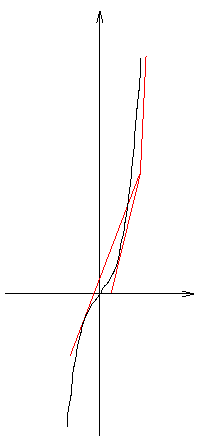
B. 3420. Keressünk olyan f:RR nem konstans függvényt, amelynek grafikonja 3-szoros nagyítással kapható a függvény négyzetének grafikonjából. (5 pont)

Javasolta: Lóczi Lajos, Budapest

Megoldás.Legyen f(x)=0, ha x negatív, és legyen 1/3, ha nemnegatív.

B. 3421. Bizonyítsuk be, hogy ha x, y, u és v olyan egész számok, amelyekre (x2+3y2)/(u2+3v2) egész, akkor alkalmas a, b egészekkel ez a hányados is felírható a2+3b2 alakban. (5 pont)

Javasolta: Csörnyei Marianna, London

Megoldás.A megoldás olvasható a KöMaL februári számában, Csörnyei Marianna cikkében.