New exercises and problems in Mathematics
December
2000
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in December 2000 |
C. 605. Solve the equation
,
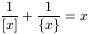where [x] and {x} denote the integer and the fractional part of x, respectively.
C. 606. A rectangular yard is tiled with identical square tiles. The tiles are arranged in 20 rows, each row containing 35 tiles. A snail is moving along a diagonal of the rectangle, starting at one vertex. Find the number of tiles crossed by the snail before it reaches the opposite vertex.
C. 607. A square of side 12 cm is rotated about a point P through an angle of 90o. The two squares cover an area of 211 cm2 altogether. A third square is obtained rotating the square further about P, again through 90o. Given also that the three squares cover an area of 287 cm2 together, determine the position of P.
Proposed by: G. Bakonyi, Budapest
C. 608. In the course of a KENO drawing, 20 winning numbers are drawn from the lot of the first 80 positive integers. Calculate the probability that none of the winning numbers contain the digit 8.
C. 609. Prove that the distance between the line 3x-4y+4=0 and a lattice point in the plane is always a rational number.
 |
New problems in Decober 2000 |
B. 3412. Prove that for all but two positive integers
q there is an integer p such that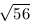 
<p/q<
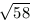. (3 points)
B. 3413. In the Hungarian Soccer League, last year still called `professional', one group comprises 8 teams. At each match one of the participating teams plays away while the other plays at home. During a season, when each team plays exactly one game with any other team, the draw of a team is called balanced if it plays alternately at home and away. Is it possible to arrange that each of the 8 teams has a balanced draw? (4 points)
B. 3414. In a cyclic quadrilateral whose diagonals are perpendicular, the sum of the squares of the edges is 8. Determine the circumradius of the quadrilateral. (3 points)
Proposed by: Á. Besenyei, Tatabánya
B. 3415. Determine all values of the parameter p for which the equation
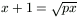
has exactly one root. (4 points)
B. 3416. Each face of a convex polyhedron is a
quadrilateral. The surface area of the polyhedron is A, the sum of the
squares of its edges is Q. Prove that Q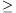
2A. (4 points)
Proposed by: Á. Besenyei, Tatabánya
B. 3417. Consider all circles in the plane whose equation
can be written in the form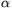 
((x-2)2+y2-1)+
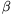((x+2)2+y2-1)=0 with suitable real numbers 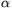, 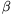. Determine the locus
of points which do not lie on any of these circles. (4 points)
B. 3418. In a triangle ABC, the medians starting at
vertices A, B, C intersect the circumcircle at points
A1, B1, C1,
respectively. Prove that tA1BC+tB1CA+tC1AB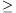tABC. (5 points)
Proposed by: I. Varga, Békéscsaba
B. 3419. Find those points in the plane through which 3 different tangents can be drawn to the curve y=x3. (4 points)
B. 3420. Find a non-constant function f:R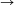
R whose graph can be obtained from the
graph of the square of the function by an enlargement of
ratio 3. (5 points)
Proposed by: L. Lóczi, Budapest
B. 3421. Assume that (x2+3y2)/(u2+3v2) is an integer number for certain integers x, y, u and v. Prove that this fraction can also be written in the form a2+3b2 with suitable integers a and b. (5 points)
Proposed by: M. Csörnyei, London
 |
New advanced problems in December 2000 |
A. 251. Given a sphere and a point P on it, let PQ denote, for any point Q not on the sphere, the second intersection of line PQ with the sphere. In the degenerate case when PQ is tangent to the sphere, let PQ=P. Prove that if points A,B,C,D of the sphere are not coplanar, then there are at most two different points Q such that the tetrahedron AQBQCQDQ is equilateral. (A tetrahedron is called equilateral if all its faces are congruent.)
A. 252. The integers a1,...,an give at least k+1 different remainders when they are divided by n+k. Prove that some of them add up to an integer divisible by n+k.
Proposed by: Gy. Károlyi and K. Podoski, Budapest
A. 253. Find all functions f: (0,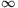
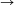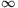)(0,) for which each
pair of positive numbers x and y satisfy
f(x)f(yf(x))=f(x+y).
International Mathematical Competition for University Students 2000, London
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.