Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A 2001. januári A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 254.  Adottak a síkon a P1, P2, ..., Pn pontok. Ezekkel a pontokkal a következő műveletet végezhetjük: Kiválasztunk egy olyan 1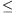i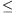n indexet, amelyre a Pi, Pi+1, Pi+2 pontok nincsenek egy egyenesen, és a PiPi+1Pi+2 háromszög negatív körüljárású. A Pi+1 pontot kicseréljük arra a pontra, amit úgy kapunk, hogy Pi+1-et tükrözzük a PiPi+2 szakaszra. Ezt a műveletet mindaddig ismételjük, amíg csak létezik megfelelő i index. Bizonyítsuk be, hogy tetszőleges pontokból kiindulva, az eljárás véges sok lépés után véget ér.

Megoldás. A feladat állítása nem igaz. Mutatunk egy olyan, 4 pontból álló példát, amikor a megadott algoritmus sohasem ér véget.

Tekintsünk egy olyan P1P2P3P4 négyszöget, amely negatív körüljárású, P1P2=1, P3P4=3, P2P3=P4P1=2 és a P2-nél levő szöge konkáv.

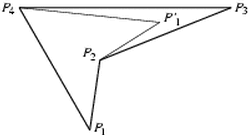
Tükrözzük a P1 pontot a P4P2 szakaszra; az így kapott pontot jelöljük P1'-vel. A P1' pont a tükrözés miatt a P4P2 egyenesnek a P3-at tartalmazó partjára esik.

Ha a P2P1' szakasznak lenne közös pontja a P3P4 szakasszal, akkor a négyszög-egyenlőtlenség alapján P2P1'+P3P4>P2P3+P1P4 teljesülne, ami nem igaz, hiszen P2P1'+P3P4=P2P3+P1P4=4. Hasonlóképpen a P4P1' és P2P3 szakaszoknak sem lehet közös pontja. Mindezekből következik, hogy a P1' pont a P2P3P4 háromszög belsejében van.

A feladatban leírt algoritmus szerint a P1 pontot kicserélhetjük a P1' pontra. Ezzel egy másik négyszöghöz jutunk, amely szintén negatív körüljárású, oldalai rendre 3, 2, 1, 2 egység hosszúak, és az 1 egységnyi oldal mellett van egy konkáv szöge. Ha mindig az egységnyi oldal hegyesszögű csúcsát tükrözzük a szemközti átlóra, minden lépésben ilyen tulajdonságú négyszögeket fogunk kapni, és így az eljárás nem ér véget.

A. 255.  Legyen 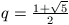, és definiáljuk a pozitív egészeken értelmezett f függvényt a következőképpen.

    1. Legyen f(1)=2;

    2. Ha f(1), ..., f(n-1)-et már definiáltuk, és az n nem szerepel ezek között, akkor legyen f(n)=f(n-1)+1;

    3. Ha f(1), ..., f(n-1)-et már definiáltuk, és az n szerepel ezek között, akkor legyen k a legkisebb pozitív egész, amelyre f(k)=n, és legyen f(n)=n+k.

Igazoljuk, hogy tetszőleges n pozitív egészre

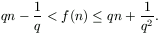
Megoldás. Az állítást teljes indukcióval igazoljuk. Az n=1 esetben \(\displaystyle f(1)=2=q\cdot1+{1\over q^2}\), vagyis az állítás igaz.

Legyen n>1, és tegyük fel, hogy az állítás minden ennél kisebb értékre igaz.

Ha n=f(k) és k a legkisebb ilyen pozitív egész, akkor a definíció 2. pontja szerint f(n)=n+k; az indukciós feltevés szerint pedig

\(\displaystyle qk-{1\over q}

Ezt átrendezve kapjuk, hogy

\(\displaystyle {1\over q}n-{1\over q^3}\le k<{1\over q}n+{1\over q^2},\)

és

\(\displaystyle \left(1+{1\over q}\right)n-{1\over q^3}={1\over q^3}\le n+k<\left(1+{1\over q}\right)n+{1\over q^2},\)

azaz

\(\displaystyle qn-{1\over q^3}\le f(n)

Ha az n nem szerepel az f(1), ...f(n-1) értékek között, akkor n\(\displaystyle ge\)4 (n=4 az első ilyen érték), és a definíció 3. pontja szerint f(n)=f(n-1)+1. A felső becslés ebből máris következik, mert az indukciós feltevés szerint

\(\displaystyle f(n)=f(n-1)+1\le q(n-1)+{1\over q^2}+1

Az alsó becslés igazolásához legyen k az a pozitív egész, amelyre \(\displaystyle {n\over q}-1k és k+1 számokra. Az indukciós feltevés szerint

\(\displaystyle f(k)\le qk+{1\over q^2}

\(\displaystyle f(k+1\)q(k+1)-{1\over q}>n-1,">

továbbá

\(\displaystyle f(k+1)-f(k)

Mivel az n nem függvényérték, a három egyenlőtlenség egyszerre csak úgy teljesülhet, ha f(k)=n-1 és f(k+1)=n+1. Az f definíciója szerint ebből f(n-1)=(n-1)+k=n+k-1 és f(n)=f(n-1)+1=n+k.

Az indukciós becslést a k+1 számra felírva

\(\displaystyle n+1=f(k+1)\le q(k+1)+{1\over q^2},\)

amiből

\(\displaystyle k\ge{1\over q}n-1+{1\over q}-{1\over q^3}\)

és

\(\displaystyle f(n)=n+k\ge n+{1\over q}n-1+{1\over q}-{1\over q^3}=qn-{1\over q}.\)

Mivel f(n) egész, a \(\displaystyle qn-{1\over q}=q(n-1)+1\) szám pedig irracionális, az egyenlőség nem lehetséges, tehát \(\displaystyle f(n\)qn-{1\over q}">.

A. 256. Van n golyó, mindegyiknek szeretnénk megtudni a súlyát. Ehhez rendelkezésünkre áll egy olyan egykarú mérleg, amellyel egyszerre egy vagy két golyó súlyának összegét lehet meghatározni. Arra is fel kell készülnünk, hogy esetleg az egyik mérés pontatlan lesz. Jelöljük f(n)-nel azt a minimális mérésszámot, amellyel az összes golyó súlya minden esetben biztosan meghatározható. Igazoljuk, hogy

f(n)<n+log3n+3.

Surányi László és Virág Bálint ötletéből

Megoldás. Számozzuk meg a golyókat 1-től n-ig; a súlyukat jelöljük x1, ..., xn-nel.

Mérjük meg először az 1, golyót, az n-edik golyót, valamint minden 1\(\displaystyle le\)i<n-re az i-edik és az (i+1)-edig golyó súlyának összegét. Jelöljük a kapott eredményeket M1-gyel, Mn-nel, illetve Mi,i+1-gyel; ez eddig n+1 mérés. Ha ezek mind pontosak, akkor M1=x1, Mn=xn és Mi,i+1=xi+xi+1, valamint

(1) M1+M2,3+M4,5+...=M1,2+M3,4+M5,6+...,

mert mindkét oldalon x1+x2+...+xn áll. (Az utolsó mérés a két összegben az egyik oldalon Mn, a másikon Mn-1,n. Hogy melyik melyik oldalon, az n paritásától függ.) Megfordítva, ha valamelyik mérésben többet vagy kevesebbet kapunk eredményül, akkor a megfelelő oldal is ugyanennyivel nagyobb vagy kisebb.

Ha mindegyik mérés pontos volt, akkor több mérésre nincs szükség, mert az összes golyó súlyát meg tudjuk határozni:

    x1=M1,
    x2=M1,2-x1=M1,2-M1,
    x3=M2,3-x2=M2,3-M1,2+M1,
    x4=M3,4-x3=M3,4-M2,3+M1,2-M1,
    ...

A továbbiakban ezért azt az esetet vizsgáljuk, amikor az egyik mérés pontatlan, azaz (1) két oldala különböző. Legyen

    y1=M1,
    y2=M1,2-M1,
    y3=M2,3-M1,2+M1,
    y4=M3,4-M2,3+M1,2-M1,
    ...,

ezen kívül legyen D (1) két oldalának különbsége:

D=M1-M1,2+M2,3-M3,4+-....

Vagy az M1, M2,3, ...mérések valamelyike D-vel nagyobb a pontos értéknél, vagy pedig az M1,2, M3,4, ...mérések valamelyike D-vel kisebb. Mindkét esetben igaz az, hogy

    1) xi=yi ha az M1, M1,2, ..., i-1,i értékek pontosak;
    2) xi=yi+(-1)i+1D, ha az M1, M1,2, ..., Mi-1,i értékek valamelyike a pontatlan.

Ha tudnánk, melyik mérés a pontatlan, akkor mindegyik golyó súlyát ki tudnánk számítani a meglevő információkból. Megmutatjuk, hogy további, legfeljebb log3n+2 méréssel meghatározhatjuk, hogy melyik volt a pontatlan mérés. A feltételek szerint ezek a további mérések már mind pontosak lesznek.

Válasszunk olyan i és j számokat, amelyekre 1\(\displaystyle le\)i<j\(\displaystyle le\)n és \(\displaystyle i\equiv j\pmod2\). Ha megmérjük az i-edik és a j-edik golyó súlyának összegét, háromféle eredményt kapunk:

1) xi+xj=yi+yj+2.(-1)i+1D, ha a pontatlan mérés M1, ..., Mi-1,i valamelyike;

2) xi+xj=yi+yj+(-1)i+1D, ha a pontatlan mérés Mi,i+1, ..., Mj-1,j valamelyike;

3) xi+xj=yi+yj, ha a pontatlan mérés Mj,j+1, ..., Mn valamelyike.

Az első (n+1) mérés mindegyike ,,gyanús''; ezek bármelyike lehet a pontatlan mérés. A továbbiakban minden lépésben kiválasztunk két, azonos paritású sorszámú golyót, ezek súlyának összegét megmérjük, és így a gyanús mérések halmazát körülbelül a harmadára fogjuk csökkenteni.

Az egyszerűbb számolás érdekében legyen N a legkisebb pozitív egész, amelyre n+1\(\displaystyle le\)2.3N. Tegyük fel, hogy egy adott helyzetben legfeljebb k\(\displaystyle le\)2.3K gyanús mérésünk van: Mm,m+1, Mm+1,m+2, ..., Mm+k-1,m+k. Legyen i=m+2.3K-1 és j=m+4.3K-1, és mérjük meg az i-edik és j-edik golyó súlyának összegét. Az összeg ismeretében eldönthetjük, hogy a hibás mérés az Mm,m+1, ..., Mi-1,i, az Mi,i+1, ..., Mj-1,j, vagy pedig az Mj,j+1, ..., Mm+k-1,m+k között van. Az új helyzetben a gyanús mérések száma legfeljebb 2.3K-1 lesz.

Összesen (n+1)+N mérés után a gyanús mérések száma legfeljebb 2.30=2. Ezután egyetlen méréssel, például a két gyanús mérés egyikének újbóli elvégzésével kiderül, melyik volt a hibás mérés. A mérések száma összesen

(n+1)+N+1<n+log3n+3.