A 2001. januári B-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B. 3422. Igazoljuk, hogy 72001-33335 osztható 100-zal. (3 pont)
Megoldás. 2001=3.667, 3335=5.667. Így
72001-33335 = (73)667-(35)667 = 343667-243667 = (343-243)(343666+343665243+...+243666).
Az első tényező éppen 100.
B. 3423. Alkothatnak-e egy háromszög beírt körének az oldalakon levő érintési pontjai tompaszögű háromszöget? (3 pont)
Megoldás. Nem. A beírt kör középpontja mindig az érintési pontok által meghatározott háromszög belsejében van, ezért ez a háromszög mindig hegyesszögű.
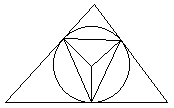
B. 3424. Egy szabályos háromszögbe négyzetet írunk, amelynek minden csúcsa a háromszög kerületén van. A négyzet egyik oldala egy kisebb szabályos háromszöget metsz le; ebbe hasonló módon ismét négyzetet írunk, és így tovább. A háromszög hányadrészét fedi le a négyszögek végtelen sorozata? (3 pont)
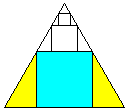
Megoldás. A négyzeteknek a háromszög oldalával párhuzamos
oldalai a háromszöget trapézokra bontják. Az ábrán az egyik ilyen
trapézt színeztük ki. Mindegyik trapéz területének 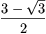 -szerese a megfelelő négyzet területe. A
négyszögek által lefedett rész tehát a teljes terület
-szerese a megfelelő négyzet területe. A
négyszögek által lefedett rész tehát a teljes terület 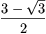 -szerese, körülbelül 63,4%-a.
-szerese, körülbelül 63,4%-a.
B. 3425. A 3+4+5+6=3.6; 15+16+17+...+34+35=15.35 egyenlőségek azt sugallják, hogy a természetes számokból ki lehet választani néhány egymás követőt úgy, hogy összegük egyenlő a legkisebb és a legnagyobb kiválasztott szám szorzatával. Mutassuk meg, hogy végtelen sok ilyen tulajdonságú sorozat van! (5 pont)
Kiss Sándor, Nyíregyháza
1. megoldás. Olyan a<b pozitív egészeket kell keresnünk, amelyekre
a+(a+1)+...+b=ab,
azaz
\(\displaystyle {(b-a+1)(a+b)\over2}=ab,\)
(1) a2+2ab-b2-a-b=0.
Tegyük fel, hogy az (a0,b0) számpár megoldása az (1) egyenletnek. Ebből további egész megoldásokat fogunk konstruálni.
Tekintsük az x2+(2b0-1)x-b02-b0=0 másodfokú egyenletet. Ennek egyik gyöke x1=a0. A másik gyöke a Viéte-képletekből x2=-(2b0-1)-a0. Ha tehát az (a0,b0) számpár megoldása az (1) egyenletnek, akkor a (-a0-2b0+1,b0) számpár is megoldás.
Tekintsük most az x2-(2a0-1)x-a02+a0=0 másodfokú egyenletet. Ennek egyik gyöke x1=b0, másik gyöke x2=(2a0-1)-b0. Tehát az (a0,2a0-b0-1) számpár is megoldása (1)-nek.
Az iménti kétféle lépést felváltva alkalmazva kapjuk, hogy a következő számpárok mind megoldásai az (1) egyenletnek:
(a0,b0);
(-a0-2b0+1,b0);
(-a0-2b0+1,-2a0-5b0+1);
(5a0+12b0-2,-2a0-5b0+1);
(5a0+12b0-2,12a0+29b0-6).
Ha a0<b0 pozitív egészek, akkor 5a0+12b0-2<12a0+29b0-6 is pozitív egészek. Így a feladat egy megoldásából egy ,,nagyobb'' megoldást konstruáltunk.
Megjegyzés. Az, hogy ha (a0,b0) megoldás, akkor (5a0+12b0-2,12a0+29b0-6) is megoldás, egyszerű behelyettesítéssel is ellenőrizhető:
(5a0+12b0-2)2+2(5a0+12b0-2)(12a0+29b0-6)-
-(12a0+29b0-6)2-(5a0+12b0-2)-
-(12a0+29b0-6)=a2+2ab-b2-a-b=0.
2. megoldás. Az (1) egyenletet átalakítva
(2a+2b-1)2-8b2=1,
ami x=2a+2b-1, y=b helyettesítéssel az x2-8y2=1 Pell-egyenlet. Ennek megoldásai mindazok az (x,y) számpárok, amelyekre \(\displaystyle x\pm2\sqrt{2}y=\big(3\pm2\sqrt{2}\big)^n\) valamely n pozitív egészre. Ebből végtelen sok megoldást nyerhetünk, például az n=2,3,4 kitevőkre a következő (a,b) számpárokat kapjuk: (3,6), (15,35), (85,204).
B. 3426. Mit kapunk maradékul, ha az x2001 polinomot elosztjuk (x+1)2-nel? (4 pont)
Megoldás. A binomiális tétel alapján
x2001=((x+1)-1)2001=
\(\displaystyle ={2001\choose0}(x+1)^{2001}-+\dots+{2001\choose2000}(x+1)-{2001\choose2001}.\)
Az utolsó kettő kivételével mindegyik tag osztható (x+1)2-nel. A maradék tehát
\(\displaystyle {2001\choose2000}(x+1)-{2001\choose2001}=2001x+2000.\)
B. 3427. Tükrözzük a hegyesszögű ABC háromszög oldalegyeneseit a rájuk nem merőleges magasságvonalakra. Az így kapott hat tükörkép közül három az ABC háromszög belsejében fekvő A1B1C1 háromszöget, míg a másik három az A2B2C2 háromszöget határolja. Ez utóbbi háromszögnek van egy 20o-os és egy 70o-os szöge. Számítsuk ki az A1B1C1 háromszögek szögeit. (4 pont)
Bakonyi Gábor, Budapest
Megoldás. Legyenek a háromszög szögei \(\displaystyle alpha\)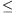
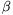
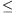
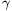 .
.
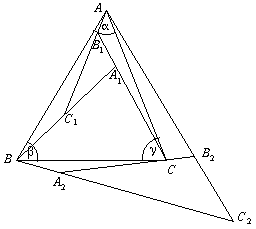
A szögek összeszámolásával ellenőrizhető, hogy az ábra szerinti
betűzéssel
C1A1B1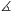 =2
=2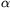 ,
A1B1C1
,
A1B1C1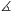 =2
=2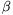 =
=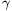 ,
B1C1A1
,
B1C1A1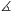 =3
=3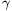 -180o,
C2A2B2
-180o,
C2A2B2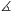 =180o-3
=180o-3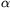 ,
A2B2C2
,
A2B2C2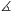 =180o+
=180o+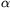 -2
-2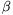 és
B2C2A2
és
B2C2A2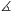 =2
=2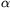 +2
+2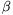 -180o.
-180o.
Az utóbbi három szög közül az egyik 20, egy másik 70 fokos, a
harmadik 90 fokos. A szögek sorrendjétől függően hat eset
lehetséges. Mindegyik esetben egy egyenletrendszer adja meg az 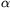 ,
, 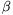 és
és 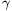 értékét.
értékét.
180o-3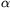 |
180o+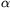 -2 -2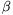 |
2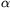 +2 +2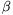 -180o -180o |
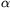 | 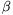 | 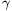 |
|
| 20o | 70o | 90o | 53 o o | 81 o o | 45o | Nem
megoldás, mert 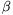 > >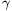 |
| 20o | 90o | 70o | 53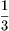 o o | 71 o o | 55o | Nem
megoldás, mert 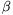 > >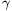 |
| 70o | 20o | 90o | 36 o o | 98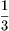 o o | 45o | Nem
megoldás, mert 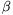 > >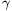 |
| 70o | 90o | 20o | 36 o o | 63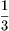 o o | 80o | Megoldás |
| 90o | 20o | 70o | 30o | 95o | 55o | Nem megoldás, mert
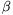 > >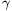 |
| 90o | 70o | 20o | 30o | 70o | 80o | Megoldás |
A feladatnak tehát kétféle megoldása van; az ABC háromszög
szögei 36 , 63
, 63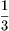 és 80, vagy pedig 30, 70 és 80 fokosak. Az eslő
esetben az
A1B1C1 háromszög
szögei 73
és 80, vagy pedig 30, 70 és 80 fokosak. Az eslő
esetben az
A1B1C1 háromszög
szögei 73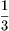 , 46
, 46 és 60 fokosak, a második esetben az
A1B1C1 háromszög
szabályos.
és 60 fokosak, a második esetben az
A1B1C1 háromszög
szabályos.
B. 3428. Bizonyítsuk be, hogy tetszőleges háromszögben érvényes az alábbi összefüggés:
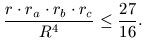
(R a háromszög köré írt, r a háromszögbe írt, ra, rb, rc pedig a hozzáírt körök sugarát jelentik.) (4 pont)
Tőricht Pál és Árokszállási Tibor, Paks
Megoldás. Jelöljük a háromszög területét t-vel,
félkerületét s-sel. Mint ismeretes,
t=r.s=ra.(s-a)=rb.(s-b)=rc.(s-c),
továbbá a Héron-képlet szerint
t2=s(s-a)(s-b)(s-c). Ezekből
következik, hogy
r.ra.rb.rc=t2. Ezt
behelyettesítve láthatjuk, hogy a bizonyítandó állítás ekvivalens az
ismert 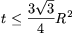 egyenlőtlenséggel.
egyenlőtlenséggel.
B. 3429. Legyen 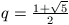 , és legyen f:N
, és legyen f:N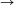 N egy olyan függvény, amelyre tetszőleges pozitív egész
n esetén
N egy olyan függvény, amelyre tetszőleges pozitív egész
n esetén
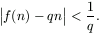
Igazoljuk, hogy f(f(n))=f(n)+n. (4 pont)
Megoldás. Tetszőleges n pozitív egészre
|f(f(n))-f(n)-n|=|f(f(n))-qf(n)+(q-1)f(n)-q(q-1)n|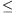
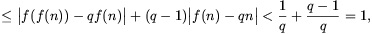
tehát f(f(n))-f(n)-n=0.
B. 3430. Adottak a síkon a P1, P2, ...,
Pn pontok. Kiválasztunk egy olyan
1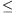 i
i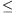 n
indexet, amelyre a Pi,
Pi+1, Pi+2 pontok nincsenek egy egyenesen, és a
PiPi+1Pi+2 háromszög negatív körüljárású. (Az indexelés
ciklikus). A Pi+1 pontot
kicseréljük arra a pontra, amit úgy kapunk, hogy Pi+1-et tükrözzük a PiPi+2
szakasz felezőpontjára. Ezt mindaddig ismételjük, amíg csak létezik megfelelő
i index. Bizonyítsuk be, hogy tetszőleges pontokból kiindulva az eljárás
véges sok lépés után véget ér. (5 pont)
n
indexet, amelyre a Pi,
Pi+1, Pi+2 pontok nincsenek egy egyenesen, és a
PiPi+1Pi+2 háromszög negatív körüljárású. (Az indexelés
ciklikus). A Pi+1 pontot
kicseréljük arra a pontra, amit úgy kapunk, hogy Pi+1-et tükrözzük a PiPi+2
szakasz felezőpontjára. Ezt mindaddig ismételjük, amíg csak létezik megfelelő
i index. Bizonyítsuk be, hogy tetszőleges pontokból kiindulva az eljárás
véges sok lépés után véget ér. (5 pont)
Megoldás. Legyenek a Pi pont koordinátái xi és yi. A P1...Pn (hurkolt) sokszög előjeles területét a következő képlettel definiálhatjuk:
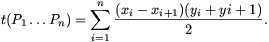
Ismeretes, hogy ez a képlet nem változik, ha a sokszöget párhuzamosan eltoljuk, más szóval, csak a sokszög oldalvektoraitól függ. Azt is könnyű ellenőrizni, hogy amikor a Pi+1 pontot tükrözzük a PiPi+2 szakaszra, akkor az előjeles terület a PiPi+1Pi+2 háromszög területének kétszeresével nő.
Az előjeles terület tehát minden lépésben nő. Ugyanakkor az oldalvektoroknak csk a sorrendje változik, mert minden lépésben két oldalvektort kicserélünk. Lépéseink során, a területnövekedés miatt, az oldalvektorok egy adott sorrendje legfeljebb egyszer fordulhat elő; ezért legfeljebb n!-1 lépést tehetünk meg a feltételeknek megfelelően.
B. 3431. OKOSBANK páncélszekrényén több különböző zár van. A bankban n pénztáros dolgozik, mindegyiknek kulcsa van a zárak némelyikéhez. (Egy pénztárosnak több kulcsa is lehet, és egy zárhoz többüknek is lehet kulcsa.) Tudjuk, hogy bármelyik k pénztáros együtt mindig ki tudja nyitni a páncélszekrényt, de k-1 pénztáros soha. Legalább hány zár van a páncélszekrényen? (5 pont)
Vígh Viktor, Szeged
Megoldás. A feltétel szerint bármely k-1 pénztároshoz van egy olyan zár, amiot egyikük sem tud kinyitni. Ha H1 és H2 pénztárosok két különböző k-1 elemű részhalmaza, akkor léteznek olyan Z1 és Z2 zárak úgy, hogy a H1-be tartozó pénztárosok nem tudják kinyitni Z1-et, a H2-be tartozók pedig Z2-t. A két halmazban összesen legalább k pénztáros van, eggyüttesen tehát mindkét zárat ki tudják nyitni.
Az eddigiekből következik, hogy a különböző, k-1
pénztárosból álló halmazokhoz különböző olyan zárak tartoznak, amit az
illető pénztárosok nem tudnak kinyitni. A zárak száma tehát legalább
annyi, mint a k-1 elemű pénztároshalmazok száma, 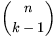 .
.
Ennyi zár elegendő is. Ha minden k-1 elemű pénztároshalmazhoz van egy zár, amit az adott pénztárosok nem tudnak kinyitni, akkor a feltételek teljesülnek.
