A 2001. januári C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 610. Az ábrán látható céltábla három koncentrikus körből és két egymásra merőleges egyenesből áll, amelyek átmennek a körök középpontján. Az így keletkezett 12 rész területe egyenlő. Adjuk meg a három kör sugarának arányát.

Megoldás. \(\displaystyle 1:\sqrt2:\sqrt3\).

C. 611.  Határozzuk meg az a, b, c, d, e számjegyeket úgy, hogy a velük felírt két ötjegyű számra teljesüljön az 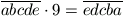egyenlőség.

Reményi Gusztáv, Budapest

Megoldás. Egy ötjegyű szám kilencszerese csak akkor lesz ötjegyű, ha az első számjegye 1. Ekkor az utolsó számjegy 9. Ahhoz, hogy az \(\displaystyle \overline{1bcd9}\) szám kilencszerese ötjegyű legyen, b-nek 0-nak vagy 1-nek kell lennie. Azt is tudjuk, hogy 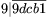, tehát (b+c+d) 9-cel osztva 8 maradékot ad. Ezekből már következtethetünk a számra, ami 10989.

C. 612. Az ABC háromszög C csúcsánál derékszög van. Jelölje D a C csúcsból az AB átfogóra bocsátott magasság talppontját. A D-ből a befogókra bocsátott merőlegesek talppontja legyen P és Q. Bizonyítsuk be, hogy a DP és a DQ szakaszok összege legfeljebb akkora, mint a befogók hosszainak harmonikus közepe.

(Az a és b számok harmonikus közepe a reciprokaik átlagának reciproka, azaz 2ab/(a+b).

Varga István, Békéscsaba

Megoldás. Legyen a háromszög oldalainak hossza AC=b, BC=a, AB=c, továbbá DP=x, DQ=y.

Azt kell igazolnunk, hogy

A Pitagorasz-tételből, valamint az ABC, ACD, CBD, ADP és CDQ háromszögek hasonlóságából 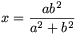és \(\displaystyle y={a^2b\over a^2+b^2}\). Ezeket behelyettesítve, a bizonyítandó állítás:

Ez, mint beszorzás és egyszerűsítés után láthatjuk, ekvivalens az (a-b)²\(\displaystyle ge\)0 egyenlőtlenséggel.

C. 613. Messe az ABC háromszög BC oldalával párhuzamos egyenes az AB oldal egyenesét a D, az AC oldal egyenesét az E pontban. Legyen M a BC oldal tetszőleges belső pontja. Mekkora az ADME négyszög területe, ha az ABC háromszög területe T, és az ADE háromszög területe t?

Besenyei Ádám, Tatabánya

Megoldás. Attól függően, hogy az egyenes a háromszög oldalegyeneseinek melyik részét metszi, több eset is lehetséges.

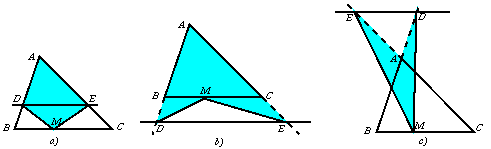
Legyen BC=a, az ABC háromszög A-ból induló magasságának hossza m. Az ABC és ADE háromszögek hasonlóak, a hasonlóság aránya \(\displaystyle \sqrt{t}:\sqrt{T}\). Ezért 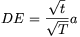, az ADE háromszög A-ból induló magassága pedig \(\displaystyle {\sqrt{t}\over\sqrt{T}}m\). A BDE háromszög M-ből induló magassága az a) esetben , a b) esetben 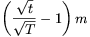, a c) esetben .

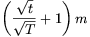Ebből rövid számolással kapjuk az ADBE négyszög területét, amely mindegyik esetben \(\displaystyle \sqrt{Tt}\).

C. 614. Az m valós paraméter mely értékeire nincs megoldása az

msin²x+(m-1)sin x+m-2=0

egyenletnek?

Reményi Gusztáv, Budapest

Megoldás. Akkor nincs megoldás, ha az

(1) my²+(m-1)y+(m-2)=0

egyenletnek nincs gyöke a [-1,1] intervallumban.

Az m=0 esetben az (1) egyenlet elsőfokú; egyetlen megoldása, y=2, az intervallumon kívül esik. Az m=0 tehát megfelelő.

A 0-tól különböző m-ekre az (1) egyenlet másodfokú. Akkor nincs megoldása a [-1,1] intervallumban, ha diszkriminánsa negatív, vagy pedig a két gyök abszolút értéke nagyobb 1-nél. Az egyenlet diszkriminánsa

Ez akkor negatív, ha \(\displaystyle m<1-{2\over\sqrt{3}}\) vagy \(\displaystyle \)1+{2\over\sqrt{3}}">.

Ha \(\displaystyle 1-{2\over\sqrt{3}}\le m\le1+{2\over\sqrt{3}}\), akkor a (2) egyenletnek két valós gyöke van: \(\displaystyle {-(m-1)-\sqrt{-3m^2+6m+1}\over2m}\) és 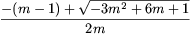. Azt kell megvizsgálnunk, hogy ezek mikor kisebbek -1-nél, illetve mikor nagyobbak 1-nél. Ez összesen négy egyenlőtlenség megoldását jelenti. A továbbiakban a

(2) \(\displaystyle {-(m-1)+\sqrt{-3m^2+6m+1}\over2m\)1">

egyenlőtlenség megoldását részletesebben tárgyaljuk, a többinek csak a végeredményét közöljük. Az m különböző értékeire a megoldás lépései különböznek egymástól. A (2) egyenlőtlenség egy lehetséges megoldását a következő táblázatban foglaltunk össze.

Eset	Megoldás
\(\displaystyle 1-{2\over\sqrt{3}}\le m<0\)	Az egyenlőtlenséget 2m-mel beszorozva (az egyenlőtlenség iránya megfordul) és rendezve \(\displaystyle \sqrt{-3m^2+6m+1}<3m-1.\) A feltétel szerint a jobboldal negatív, így ez az egyenlőtlenség az intervallum semelyik pontjában sem teljesül.
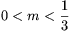	2m-mel szorozva és rendezve \(\displaystyle \sqrt{-3m^2+6m+1\)3m-1."> A 3m-1 kifejezés a teljes intervallumban negatív, ezért az egyenlőtlenség teljesül.
\(\displaystyle {1\over3}\le m\le1+{2\over\sqrt{3}}\)	Beszorozva és rendezve \(\displaystyle \sqrt{-3m^2+6m+1\)3m-1."> A megadott intervallumban mindkét oldal nemnegatív, ezért négyzetre emelhetünk: -3m2+6m+1>9m2-6m+1 m(m-1)<0 Ez akkor teljesül, ha m<1.

Összefoglalva, az \(\displaystyle {-(m-1)+\sqrt{-3m^2+6m+1}\over2m\)1"> egyenlőtlenség akkor teljesül, ha 0<m<1.

A további három egyenlőtlenség megoldását a következő táblázatban foglaltuk össze.

\(\displaystyle {-(m-1)+\sqrt{-3m^2+6m+1}\over2m\)1">	0<m<1
\(\displaystyle {-(m-1)+\sqrt{-3m^2+6m+1}\over2m}<-1\)	\(\displaystyle 1-{2\over\sqrt{3}}\le m<0\)
\(\displaystyle {-(m-1)-\sqrt{-3m^2+6m+1}\over2m\)1">	Sehol sem teljesül
\(\displaystyle {-(m-1)-\sqrt{-3m^2+6m+1}\over2m}<-1\)	\(\displaystyle 1-{2\over\sqrt{3}}\le m<0\) vagy 0<m<1

A táblázatból látható, hogy \(\displaystyle 1-{2\over\sqrt{3}}\le m<0\) és 0<m<1 esetén esik az (1) egyenlet mindkét gyöke a [-1,1] intervallumon kívül.

Eredményeinket összegezve, az (1) egyenletnek akkor nincs megoldása a [-1,1] intervallumban, ha m<1 vagy \(\displaystyle \)1+{2\over\sqrt{3}}">.

Megjegyzés. Egy másik lehetséges megoldás az (1) egyenletet következő átrendezésén alapul:

Az f:[0,1]\(\displaystyle arrow\)R, \(\displaystyle f(y)={y+2\over y^2+y+1}\) függvény vizsgálatával ellenőrizhető, hogy ennek a függvénynek az értékkészlete az \(\displaystyle \left[1,1+{2\over\sqrt{3}}\right]\) intervallum. Az ezen kívül eső m-ekhez nem létezik megfelelő y.