A fizika elméleti feladatok megoldása, 2001. január

A 2001. januári számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3394. Két autó indul el azonos időpontban, ugyanarról a helyről. Az egyik sebessége 60 km/h, a másik sebessége 80 km/h. Lehetséges-e, hogy az alábbi sebességgel távolodnak egymástól:

a) 140 km/h;

b) 20 km/h;

c) 100 km/h? (3 pont)

Közli: Pécsi István, Szolnok

Megoldás: Igen. A távolodás sebessége 140 km/h, ha egymással ellentétes irányba haladnak; 20 km/h, ha azonos az irányuk; míg 100 km/h, ha a haladási irányok merőlegesek egymásra.

P. 3395. Egy acél repülőgép-anyahajó hossza a 0 ^oC-os Jeges-tengeren 600 m. Milyen hosszú lesz ugyanez a hajó a 20 ^oC-os Földközi-tengeren? (3 pont)

Közli: Radnóti Katalin, Budapest

Hányszorosára változik a hajó vízbe merülő részének térfogata? (+2 pont)

Megoldás:

l=l₀(1+$\displaystyle alpha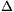$ Delta T).

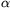Vasra alpha =1,17^.10^-5 K^-1, ahonnan l=600,14 m.

Kihasználva, hogy a kiszorított víz tömege (a hajó tömege) változatlan

${V_{20}\over V_0}={\rho_0\over\rho_{20}}.$

Mivel (a só hatását elhanyagolva) 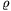rho ₀=999,87 kg/m³ és 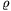rho ₂₀=998,23 kg/m³, V₂₀/V₀=1,0016.

P. 3396. Az A és B pontokból egyszerre indítunk el egy-egy testet. Az A pontból induló test kezdősebesség nélkül lecsúszik a h=1 m magas lejtőn, a B pontból indulót ferdén elhajítjuk. A két test egyszerre és ugyanakkora nagyságú sebességgel csapódik be a C pontban. Milyen hosszú a lejtő? (A közegellenállás és a súrlódás elhanyagolható.) (5 pont)

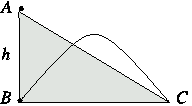
OKTV feladat nyomán

Megoldás: A lejtő tetejéről indított test végsebessége és csúszási ideje:

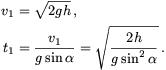
$\eqalign{v_1&=\sqrt{2gh}\,,\cr t_1&={v_1\over g\sin\alpha}=\sqrt{2h\over g\sin^2\alpha}\,.\cr}$

A beta 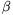szög alatt v₂ sebességgel elhajított test akkor repül l=h/ 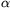alpha távolságra, ha

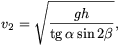
$v_2=\sqrt{gh\over\tg\alpha\sin2\beta},$

ekkor a repülési idő

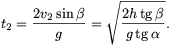
$t_2={2v_2\sin\beta\over g}=\sqrt{2h\tg\beta\over g\tg\alpha}.$

Ha v₁=v₂ és t₁=t₂, akkor

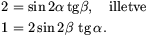
$\eqalign{2&=\sin2\alpha\,{\tg}\beta,\quad{\rm illetve}\cr1&=2\sin2\beta\,\tg\alpha.\cr}$

Ezek az egyenletek a

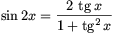
$\sin2x={2\,\tg x\over1+\tg^2x}$

összefüggés segítségével megoldhatók:

$\tg\alpha=\sqrt{{\sqrt{13}-1\over6}}=0{,}659,\qquad\alpha=33{,}38^{\circ},$

és

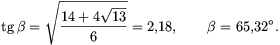
$\tg\beta=\sqrt{14+4\sqrt{13}\over6}=2{,}18,\qquad\beta=65{,}32^{\circ}.$

Innen a lejtő alapjának hossza l=1,517 m.

P. 3397. Az ábrán látható merev, L=2 m hosszú rúd A végpontja állandóan az x tengelyen, B végpontja pedig az y tengelyen mozog. Az A pont sebessége állandó: v_A=1 m/s, és t=0-kor a rúd függőleges.

Határozzuk meg a B pont sebességét, gyorsulását és a rúd szöggyorsulását az idő függvényében. Mekkorák ezek az értékek az alábbi időpillanatokban: t₁=0,5 s, t₂=1,5 s és t₃=1,999 s? (A feladat elemi úton is megoldható.) (5 pont)

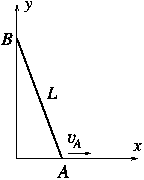
Közli: Holics László, Budapest

Megoldás: A rendszert az A ponthoz rögzített koordinata-rendszerben írjuk le. Ebben a fal v_A sebességgel balra mozog, a B pont sebessége pedig merőleges rúdra. Innen a B pont függőleges sebessége (a sebesség a nyugvó rendszerben)

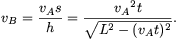
$v_B={v_As\over h}={{v_A}^2t\over\sqrt{L^2-(v_At)^2}}.$

(Itt h a B pont magassága, s pedig a vízszintes elmozdulása a mozgó rendszerben.) A rúd szögsebessége:

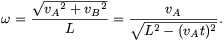
$\omega={\sqrt{{v_A}^2+{v_B}^2}\over L}={v_A\over\sqrt{L^2-(v_At)^2}}.$

A B pont a_B gyorsulása az a_t=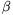 beta L érintőleges és a_r= 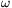omega ²L sugár irányú gyorsulások eredője. Mivel a_B függőleges

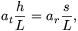
$a_t{h\over L}=a_r{s\over L},$

ahonnan

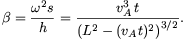
$\beta={\omega^2s\over h}={v_A^3\,t\over\left({L^2-(v_At)^2}\right)^{3/2}}.$

Hasonlóan:

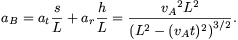
$a_B=a_t{s\over L}+a_r{h\over L}={{v_A}^2L^2\over\left({L^2-(v_At)^2}\right)^{3/2}}.$

Adatainkkal:

	t₁=0,5 s	t₂=1,5 s	t₃=1,999 s
v_B [m/s]	0,258	1,13	31,61
a_B [m/s²]	0,55	1,73	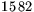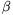$15\,82$
[1/s²]	0,069	0,65	7904,7

Megjegyzés: A szingularitás miatt nyilván valami hamarabb elromlik: ha a rúd csak neki van támasztva a falnak, előbb-utóbb elhagyja azt; ha pedig valami csúszkához van rögzítve, egyre nagyobb erő kell az egyenletes sebesség fenntartásához. (A súlypont ugyan nem gyorsul, de a forgás szögsebessége igen, ehhez egyre nagyobb forgatónyomaték kell, ami az A pontban ható húzóerőből és a falicsúszka visszahúzó erejéből adódik.

P. 3398. Egy korong egyik esetben csak forgó mozgást végez függőleges tengelye körül, másik esetben csak haladó mozgást végez vízszintesen. A két mozgás energiája azonos. A korongot lapjával vízszintes asztalra helyezzük. Melyik esetben áll meg hamarabb? Hányszor hamarabb? (Feltételezhetjük, hogy a korong egyenletesen nyomja az asztalt.) (5 pont)

Közli: Simon Péter, Pécs

Megoldás: A forgás nélkül haladó korong mozgási energiája 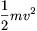${1\over2}mv^2$ , a középpontja körül forgóé 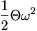${1\over2}\Theta\omega^2$ , ahol 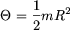$\Theta={1\over2}mR^2$ . A kettő egyenlőségéből

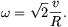
$\omega=\sqrt{2}{v\over R}.$

A tisztán csúszó korongot F=mg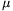 erő fékezi. A forgó korongot fékező forgatónyomaték kiszámításához osszuk fel a korongot n egyenlő (R/n) vastagságú körgyűrűre. Egy-egy ilyen gyűrűben a forgatónyomaték értéke jó közelítéssel állandó (minél nagyobb n, annál jobb a közelítés), a középtől számított k-adikban:

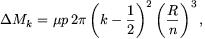
$\Delta M_k=\mu p\,2\pi\left(k-{1\over2}\right)^2\left({R\over n}\right)^3,$

ahol a nyomás p=mg/(R²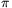). A teljes forgatónyomaték tehát

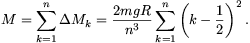
$M=\sum_{k=1}^n\Delta M_k={2mgR\over n^3}\sum_{k=1}^n\left(k-{1\over2}\right)^2.$

Mivel

$\sum_{k=1}^nk^2={n(n+1)(2n+1)\over6},\qquad{\rm illetve}\qquad\sum_{k=1}^nk={n(n+1)\over2},$

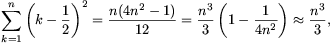
$\sum_{k=1}^n\left(k-{1\over2}\right)^2={n(4n^2-1)\over12}={n^3\over3}\left(1-{1\over4n^2}\right)\approx{n^3\over3},$

így

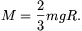
$M={2\over3}mgR.$

A haladó- illetve a forgómozgás lefékeződéséhez szükséges idők rendre

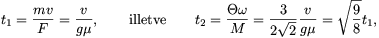
$t_1={mv\over F}={v\over g\mu},\qquad{\rm illetve}\qquad t_2={\Theta\omega\over M}={3\over2\sqrt{2}}{v\over g\mu}=\sqrt{9\over8}t_1,$

tehát a tisztán haladó mozgást végző korong áll meg hamarabb.

P. 3399. Az ábrán látható kerethez nyújthatatlan cérnából kötött hurkot erősítünk és a keretnél fogva szappanoldatba mártjuk. Ha a hurokban levő hártyát kiszúrjuk, a hurok körré feszül ki. Mekkora erő ébred a cérnában, ha a kör sugara 1 cm, az oldat felületi feszültsége 0,03 N/m? (4 pont)

Közli: Sári Péter, Budapest

Megoldásvázlat:

F=2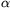 alpha r=10^-4 N

P. 3400. Acetilén gázzal (c_p/c_V=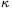=1,25) az ábra szerinti ABCDA körfolyamatot végezzük. Határozzuk meg, hogy a körfolyamat izochor szakaszában a gáz által a környezetnek leadott energia hányszorosa a körfolyamat izobár szakaszán végzett tágulási munkának? (4 pont)

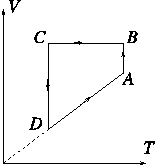
Közli: Légrádi Imre, Sopron

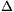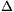Megoldásvázlat: A BC szakasz izochor, a leadott hő c_vT ( Delta T=T_B-T_C=T_A-T_D). A DA szakasz izobár, a felvett hő c_p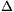T, ebből a tágulási munka (c_p-c_v) 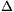Delta T. A kérdéses hányados tehát

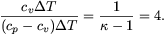
${c_v\Delta T\over(c_p-c_v)\Delta T}={1\over\kappa-1}=4.$

P. 3401. Három azonos, T területű fémlap d₁ és d₂ távolságra helyezkedik el egymástól. Az A jelű fámlap töltetlen, a B és C fémlapok töltése +q és -q. Egy adott pillanatban a K kapcsoló segítségével az A és C fémlapokat egy ismeretlen ellenállású fogyasztón keresztül összekapcsoljuk. Mekkora energiát ad le a fogyasztó a környezetének? (5 pont)

Közli: Kotek László, Pécs

Megoldás: Az AB illetve BC kapacitások értéke C_AB=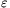 epsilon ₀T/d₁ es C_BC= 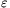epsilon ₀T/d₂. A kapcsoló zárásakor a -q töltés úgy oszlik meg az A és a C fegyverzeteken, hogy az AB és a BC kondenzátorok feszültsége egyforma legyen. Innen

$q_A={-qd_2\over d_1+d_2},\qquad q_C={-qd_1\over d_1+d_2}.$

A terhelésen hő formájában leadott energia a kezdeti E_k=q²/(2C_BC) és a végső E_v=q_A²/(2C_AB)+q_C²/(2C_BC) különbsége, azaz

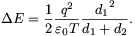
$\Delta E={1\over2}{q^2\over\varepsilon_0T}{{d_1}^2\over d_1+d_2}.$

P. 3402. Ugyanakkora erő hat-e két áramjárta vezető, illetve egy árammal átjárt vezető és egy vele párhuzamos elektronsugár között, ha a többi adat megegyezik? (4 pont)

Közli: Kovács Gyula, Gyömrő

Megoldás: Nem! Az áram által átjárt vezetők semlegesek, közöttük csak a Lorentz-erő hat. A katódsugár (elektronsugár) töltése negatív, elektromosan megosztja a vezetőt, ezért a katódsugár és a vezető között a mágneses Lorentz-erőn kívül elektromos vonzás is fellép. (Ez egyébként akár nagyobb effektus is lehet, mint a mágneses.)

P. 3403. Egy űreszközt szeretnénk a Földről a Marsra eljuttatni úgy, hogy a lehető legkevesebb energiát kelljen befektetnünk. A Földhöz képest mekkora sebességgel kell kilőnünk ezt az eszközt, és a kilövéskor mekkorának kell lennie a Föld--Nap--Mars szögnek? (A Föld és a Mars gravitációs vonzását az objektum pályájának módosításában ne vegyük figyelembe!) (6 pont)

Közli: Nagy Ádám, Budapest, Szent István Gimn.

Megoldás: A pálya optimalizálásakor két szempont játszik szerepet: (i) A Mars elérésekor a szondának feltehetően marad még mozgási energiája, ez annál nagyobb, minél ,,kerekebb'' a pálya. (ii) Az űrszondát a Földhöz képest kell felgyorsítani, így a Föld sebesége segítheti, de nehezítheti is a pályára állást.

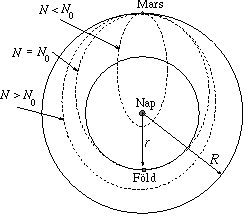
Az optimális átszállópálya nyilván olyan, hogy a Mars pályáját csak érinti, azaz a sebességnek ott csak érintőleges (tangenciális) komponense van. Paraméterezzük ezeket a pályákat a szonda N perdületével (impulzusmomentumával), ami a szonda tömegének, az előbb említett sebességnek és a Mars-pálya sugarának a szorzata! (Az N a pályára jellemző állandó, míg a sebesség a pálya mentén változik!) Ebben a paraméterezésben az energia

$E(N)=-{\gamma Mm\over R}+{N^2\over2mR^2}.$

Itt M a Nap, m a Marsra juttatandó objektum tömege és R a Mars-pálya sugara. E(N) kifejezhető a pálya a fél-nagytengelyével is:

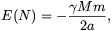
$E(N)=-{\gamma Mm\over2a},$

így összefüggést kapunk az N és a között. Eszerint amíg

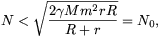
$N<\sqrt{{2\gamma Mm^2rR\over R+r}}=N_0,$

(ahol r a Föld-pálya sugara,) addig a<(R+r)/2, azaz az N-nel jellemzett pálya metszi a Földét, míg az N₀-hoz tartozó pálya éppen érinti azt. Ezért csak a 0<N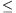N₀ tartományt kell vizsgálnunk.

Legyen a Föld-pálya és az átszálló pálya metszésében a Föld sebessége v, az űrszonda sebessége w, a pályák érintői által bezárt szög pedig 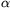alpha .

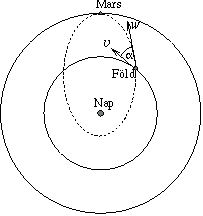
A szondát a Földhöz képest (!) akkora sebességre kell gyorsítani, melyenek a Föld-pályával párhuzamos és arra merőleges komponensei rendre w₁=w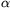 alpha -v és w₂=w 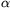alpha . Ennek megfelelően az energiaszükséglet

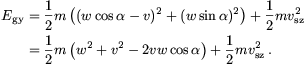
$\eqalign{E_{\rm gy}&={1\over2}m\left((w\cos\alpha-v)^2+(w\sin\alpha)^2\right)+{1\over2}mv_{\rm sz}^2\cr&={1\over2}m\left(w^2+v^2-2vw\cos\alpha\right)+{1\over2}mv_{\rm sz}^2\,.\cr}$

(Itt v_sz a Földről való szökési sebesség.)

A pálya energia és az impulzusmomentum segítségével a w² és a w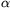 alpha megadható:

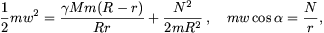
${1\over2}mw^2={\gamma Mm(R-r)\over Rr}+{N^2\over2mR^2}\,,\quad mw\cos\alpha={N\over r},$

így a minimalizálandó energia

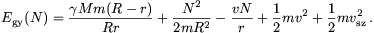
$E_{\rm gy}(N)={\gamma Mm(R-r)\over Rr}+{N^2\over2mR^2}-{vN\over r}+{1\over2}mv^2+{1\over2}mv_{\rm sz}^2\,.$

Ez N-nek egy kvadratikus kifejezése, melynek

$N^*={mvR^2\over r}$

értéknél van minimuma, így az az N<N^* értékekre monoton csökkenő. Mivel N₀<N^* a 0<N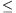N₀ pályák közül az N=N₀ pálya az optimális. Ezt a pályát Hohmann-ellipszisnek is nevezik.

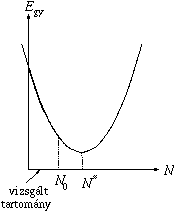
mellett a pálya nagytengelye éppen R+r, azaz az átszálló pálya a Mars-pálya mellett a Föld-pályát is csak érinti, és a két érintési pont a nagytengely két átellenes végpontja. Megjegyzendő, hogy ez a Földröl indítható, Mars-pályát érintő pályák közül a maximalis (!) energiájú, viszont ebben az esetben lehet a legjobban kihasználni a Föld sebességét a pályára állaskor. N₀ értékét behelyettesítve némi átalakítások után

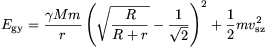
$E_{\rm gy}={\gamma Mm\over r}\left(\sqrt{{R\over R+r}}-{1\over\sqrt{2}}\right)^2+{1\over2}mv_{\rm sz}^2$

amiből a szükséges kezdősebesség 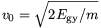$v_0=\sqrt{2E_{\rm gy}/m}$ =4,34^.10⁴ m/s.

A legyen a szonda keringési ideje T, a Marsé T_M. A szonda pont T/2 ideig repül, enyivel kell a kilövéskor a Marsnak a talákozási ponthoz (A Földdel átellenes ponthoz) képest lemaradni. Eszerint a kilövéskor a Föld-Nap-Mars szög

$\pi\left(1-{T\over T_M}\right)=\pi\left(1-\left({R+r\over2R}\right)^{3/2}\right)=0{,}7737~{\rm rad}=44{,}33^{\circ}.$

Már regisztráltál?
Új vendég vagy?