New exercises and problems in Mathematics
January 2001

Please read The Conditions of the Problem Solving Competition.

New exercises in January 2001

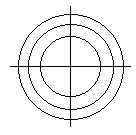
C. 610. The target on the diagram consists of three concentric circles and two perpendicular lines crossing at the common centre of the circles. Given that the respective areas of the twelve regions are equal find the ratios of the radii of the circles.

C. 611. Find the decimal digits a, b, c, d, e if the two numbers formed by these digits satisfy the equality .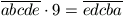

C. 612. Triangle ABC is right angled at C. The foot of the altitude from C is D and the feet of the perpendiculars from D on the legs are P and Q respectively. Show that DP+DQ does not exceed the harmonic mean of the legs. (The harmonic mean of two numbers a and b is the reciprocal of the average of their reciprocals, i.e., H(a,b)=2ab/(a+b).)

I. Varga, Nagyszalonta

C. 613. The line parallel to the side BC of the triangle ABC intersects the lines AB and AC at the points D and E respectively. Let M be an arbitrary point interior to the side BC. Given that the areas of the triangle ABC and ADE are T and t respectively, find the area of the quadrilateral ADME.

C. 614. Find those values of the real parameter m for which the following equation has no solution.

msin ²x+(m-1)sinx+m-2=0. 

G. Reményi, Budapest

New problems in Decober 2000

B. 3422. Show that 7²⁰⁰¹-3³³³⁵ is divisible by 100. (3 points)

B. 3423. Is it possible that the points of tangency of the incircle of a triangle form an obtuse triangle? (3 points)

B. 3424. A square is inscribed in an equlateral triangle in such a way that its vertices are on the perimeter of the triangle. One side of the square is the side of a smaller equilateral triangle where there is a smaller square inscribed similarly to the first one. Proceeding endlessly with smaller and smaller squares what is the ratio of the total area covered by the squares and that of the triangle. (3 points)

B. 3425. Consider the following equalities: 3+4+5+6=3^.6; 15+16+...+34+35=15^.35. They provide examples for sequences of consecutive integers whose sum is equal to the product of the first and the last terms. Prove that there are infinitely many finite sequences of this property. (5 points)

S. Kiss, Nyíregyháza

B. 3426. Find the remainder when the polynomial x²⁰⁰¹ is divided by (x+1)². (4 points)

B. 3427. Reflect each side of the acute angled triangle ABC through the two altitudes that are not perpendicular to the respective sides. Three of the six mirror images thus produced form a triangle A₁B₁C₁ in the interior of the triangle ABC while the remaining three lines form the triangle A₂B₂C₂. The measures of two angles of the latter triangle are 20^o and 70^o respectively. Find the angles of the triangle A₁B₁C₁. (4 points)

G. Bakonyi, Budapest

B. 3428. Show that the following relation holds in any triangle:

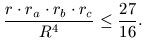
(R is the circumradius, r is the inradius and r_a, r_b and r_c denote the radii of the excircles respectively.) (4 points)

P. Tőricht and T. Árokszállási, Paks

B. 3429. Let 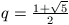and let f:N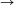N be a function satisfying

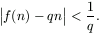
for every n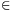N. Prove that f(f(n))=f(n)+n. (4 points)

Solution

B. 3430. Given are the points P₁, P₂, ..., P_n in the plane. Subscript i is called wrong if the corresponding point P_i is not incident to the line connecting its neighbours P_i-1 and P_i+1 and, additionally, the orientation of the triple P_i-1, P_i, P_i+1 in this order is negative. For any wrong subscript i the point P_i+1 can be replaced by its mirror image through the midpoint of the segment P_iP_i+2. This operation can be performed as long as there are wrong subscripts. (The subscripts are used in the usual cyclic manner, i.e. P_n+1=P₁, P₀=P_n, etc.) Show that no matter how the points are given the above procedure terminates. (5 points)

B. 3431. The supersafe of TweedleBank is furnished with several locks. There are n tellers working in the Bank and each of them is holding some keys for the safe. Any teller can have more than one keys and there might also be locks for which there are more than one tellers are provided with a key. Given that any k tellers are able to open the safe together but there are no k-1 of them who can do this find the minimum number of locks on the safe. (5 points)

V. Vígh, Szeged

New advanced problems in January 2001

A. 254. Given are the points P₁, P₂, ..., P_n in the plane. Subscript i is called wrong if the corresponding point P_i is not incident to the line connecting its neighbours P_i-1 and P_i+1 and, additionally, the orientation of the triple P_i-1, P_i, P_i+1 in this order is negative. For any wrong subscript i the point P_i+1 can be replaced by its mirror image through the segment P_iP_i+2. This operation can be performed as long as there are wrong subscripts. (The subscripts are used in the usual cyclic manner, i.e. P_n+1=P₁, P₀=P_n, etc.) Show that no matter how the points are given the above procedure terminates.

A. 255. Let 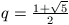and define the function f on the set of positive integers as follows.

Start with f(1)=2 and let n>1.

If the values f(1), ..., f(n-1) have already been defined and n is not among these values then set f(n)=f(n-1)+1;

otherwise consider k, the smallest positive integer, for which f(k)=n and let f(n)=n+k.

Prove that

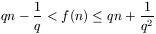
for any positive integer n.

A. 256. n marbles are to be measured with the help of a one-armed balance. We are allowed to measure one or two marbles at a time. It may happen, however, that one of the results is misread. Denote by f(n) the minimum number of weighings neccessary to determine the weight of each marble. Prove that

f(n)<n+log₃n+3.

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary

or by e-mail to: solutions@komal.elte.hu.

Deadline: 15 February 2001