A fizika elméleti feladatok megoldása, 2001. február

A 2001. februári számban kitűzött fizika elméleti feladatok megoldásai

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3404. Belül üres alumíniumgolyó 20,0 ^oC-os vízben lebeg. A vizet a golyóval együtt melegíteni kezdjük. Nő vagy csökken ekkor a golyóra ható felhajtóerő? Miért? (3 pont)

Tarján Imre emlékverseny, Szolnok

Megoldás. A víz hőtágulási együtthatója nagyobb, mint az alumíniumé, ezért melegíteskor jobban ,,ritkul'', mint az alumínium, tehát a felhajtóerő csökken.

P. 3405. A robogók rugózását gyakran az ábrán látható változó menetemelkedésű csavarrugóval oldják meg. Mi az előnye ennek a rugónak? (4 pont)

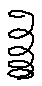
Közli: Honyek Gyula, Budapest

Megoldás. A változó menetemelkedésű rugó összenyomáskor nem követi a Hooke-törvényt: kis összenyomáskor lágyabb, nagy öszenyomás esetén viszont keményebb. Ilyenkor ugyanis a kis menetemelkedésű rész már teljesen összenyomódik (a menetek összeérnek), a maradék rész viszont mindig keményebb, mint az egész rugó. Ezzel elérhető, hogy a kis úthibákra lágyan, a nagyokra keményen reagáljon a robogó.

P. 3406. Milyen magasra ér fel az a rakéta, amit az első kozmikus sebességgel függőlegesen lőnek ki a Föld felszínéről? (4 pont)

Schwartz Lajos emlékverseny, Nagyvárad

Megoldás. Éppen egy Föld-sugárnyira a Föld felszínétől (ha a Föld forgását nem vesszük figyelembe).

P. 3407. Az ábrán felülnézetben látható elrendezésben egymásra tettünk három ugyanolyan méretű, de különböző tömegű, homogén tömegeloszlású rudat. A rudak egyik vége egy-egy oszlopra, másik vége mindig egy másik rúd közepére támaszkodik. Az oszlopok egyforma magasak. Mekkora erővel nyomják a rudakat? (Legyen m₁=1 kg, m₂=2 kg, m₃=3 kg.) Változik-e az eredmény, ha két rudat felcserélünk? (5 pont)

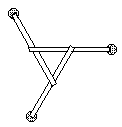
Közli: Sári Péter, Budapest

Megoldás. Azt kell kihasználni, hogy mindegyik rúd ugyanakkora erővel nyomja az oszlopot, mint annak a rúdnak a közepet, amelyikre támaszkodik. Ebből az $\displaystyle alpha$ jelű rúd által a megfelelő oszlopra gyakorolt erőre az

$\displaystyle F_{\alpha}={4\over7}m_{\alpha}g+{2\over7}m_{\gamma}g+{1\over7}m_{\beta}g$

általános megoldás adódik, ahol a $\displaystyle gamma$ rúd támaszkodik $\displaystyle alpha$ -ra, az pedig a $\displaystyle beta$ -ra. Két eset lehetséges: a) m₁ támaszkodik az m₂-re, az pedig az m₃-ra, illetve b) m₁ támaszkodik az m₃-ra, az pedig az m₂-re. A megoldások rendre:

$\displaystyle a:\quad\quad F_2={120\over7}{\rm N},\quad F_2={130\over7}{\rm N},\quad F_3={170\over7}{\rm N},$

illetve

$\displaystyle b:\quad\quad F_1={110\over7}{\rm N},\quad F_2={150\over7}{\rm N},\quad F_3={160\over7}{\rm N}.$

P. 3408. Nagyon érzékeny mérlegen lemérjük egy levegővel felfújt léggömb súlyát. Ezután kiengedjük a levegőt, és lemérjük az üres léggömb (és a madzag) súlyát. Mit tapasztalunk? Miért? (4 pont)

Lánczos Kornél verseny, Székesfehérvár

Megoldás. A felfújt lufi esetében a mérleg nagyobb értéket mutat, mert ekkor a lufiban levő levegő sűrűbb, mint a kinti, így a benti levegő súlyát nem egyenlíti ki a felhajtóerő.

P. 3409. Ideális gázzal végzett nyitott folyamatot a (V,T) diagramon egy egyenes szakasz ábrázolja. Milyen esetekben lehet a szakasz felezőpontjában a nyomás a kezdő- és végállapot nyomásának számtani közepe? (5 pont)

Közli: Légrádi Imre, Sopron

Megoldás. Ha a folyamat izobár, vagy ha izochor. Az első esetben a folyamatot egy (az origón átmenő) egyenes egy szakasza adja meg, és a nyomások (mivel azonosak) nyilvan megfelelnek a feltételnek. A második esteben a folyamatot egy (a T tengellyel párhuzamos) szakasz adja meg, e mentén pedig a nyomás arányos a T-vel.

P. 3410. Síkkondenzátor lemezei között olyan homogén E elektromos és az ábra síkjára merőleges homogén B mágneses mező van, hogy a lemezekkel párhuzamosan belőtt pozitív töltésű részecskék irányváltoztatás nélkül érik el az ernyőt. A síkkondenzátor lemezeinek hossza b, az ernyő c távolságra van a lemezek jobb oldali végétől. Ha a mágneses mezőt kikapcsoljuk, a töltött részecskék becsapódási pontja az ernyőn y-nal elmozdul. Határozzuk meg a részecskék Q/m fajlagos töltését! (A nehézségi erő hatásától tekintsünk el!) (5 pont)

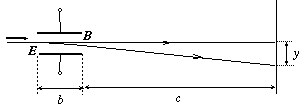
Közli: Kotek László, Pécs

Megoldás. Abból, hogy a mágneses mező jelenlétében a részecskék nem térülnek el, tudjuk, hogy a vízszintes sebességük v_v=E/B. A tér kikapcsolása után a kondenzátor lemezei között b/v_v idő alatt átrepülő részecskék az elektromos tér hatására v_f=(Q/m)Eb/v_v függőleges sebességre tesznek szert. A geometriából következik, hogy v_v:v_f=(b/2+c):y. Ezekből az összefüggésekből a fajlagos töltés:

$\displaystyle {Q\over m}={Ey\over B^2b(b/2+c)}.$

P. 3411. N menetes, r sugarú lapos tekercset egy hosszú, egyenes vezetőtől l távolságra helyezünk el (l<<r). A lapos tekercs és az egyenes vezető egy síkban vannak. Az egyenes vezetőbe egy voltmérőt iktatunk, távoli végeit pedig leföldeljük. Mit mutat a voltmérő, ha a tekercs áramát t₀ idő alatt egyenletesen nulláról I₀-ra növeljük?

Adatok: N=100, l=100 cm, r=2 cm, t₀=5 s, I₀=2 A. (5 pont)

(Lásd a Kölcsönös indukció c. cikket lapunk 110. oldalán.)

Közli: Gnädig Péter, Budapest

Megoldás. A mért feszültség nagysága

U=MI₀/t₀,

ahol M a lapos tekercsnek a végtelenül hosszúnak tekinthető egyenes vezetőre vonatkoztatott kölcsönös indukciós együtthatója. Ezt nehéz számolni, de tudjuk (a feladat kitűzésekor emlÍtett cikkből), hogy megegyezik a hosszú vezető lapos tekercsre vonatkoztatott kölcsönös indukciós együtthatójával, ami viszont könnyen számolható. Ehhez tegyük fel, hogy az egyenes vezetőben az áram $\displaystyle Delta$ I/ $\displaystyle Delta$ t ütemben változik. 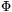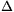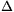Ekkor a tekercs belsejeben $\displaystyle Delta$ B/ $\displaystyle Delta$ t=( $\displaystyle mu$ ₀/2 $\displaystyle pi$ l) $\displaystyle Delta$ I/ $\displaystyle Delta$ t, tehát a tekercs fluxusának változási üteme $\displaystyle Delta$ Phi / Delta t=(₀r²/2l) Delta I/ Delta t. Mivel az indukált feszültség nagysága N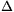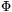/ Delta t, a keresett kölcsönös indukciós együttható M=₀Nr²/2l. Adatainkkal U=1,01^.10^-8V.

P. 3412. Keresztezett állású polárszűrőkön nem jut át a fény. Ha közéjük becsúsztatunk egy harmadik polárszűrőt, valamennyi fény átjuthat. A bejövő fénynek legfeljebb hányad része juthat át? (5 pont)

Közli: Radnai Gyula, Budapest

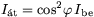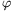Megoldás. Egy polárszűrőn átmenő fény intenzitása $I_{\rm\acute{a}t}=\cos^2\!\varphi\,I_{\rm be}$ (itt phi a beeső fény polarizációs sikjának és a szűrő által kijelölt polarizációs síknak a szöge, I_be pedig a beeső fény intenzitása.) Ennek megfelelően, ha a beeső fény polarizációs síkja az első szűrőével 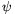$\psi$ szöget zár be, az első és a középső szűrők polarizációs síkjai pedig 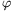phi szöget, akkor az átmenő fény intenzitása 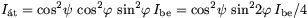$I_{\rm\acute{a}t}=\cos^2\!\psi\,\cos^2\!\varphi\,\sin^2\!\varphi\,I_{\rm be}=\cos^2\!\psi\,\sin^2\!2\varphi\,I_{\rm be}/4$ . 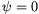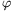Ez nyilván akkor a legnagyobb, ha $\psi=0$ és phi =45^o. 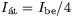Ilyenkor $I_{\rm\acute{a}t}=I_{\rm be}/4$ .

P. 3413. Ha egy fényes kanálba annak homorú oldala felől belenézünk, fejreállva látjuk magunkat. Megfordítva a kanalat, a domború oldala felől nézve egyenes állásban látjuk magunkat, de úgy tűnik, hogy ugyanakkorának, mint az előbb. Próbáljuk ki, és magyarázzuk meg a jelenséget! (4 pont)

Közli: Tichy Géza, Budapest

Megoldás. Az első esetben a kanál mint homorú tükör által létrehozott valódi képet látjuk, a másodikban a kép virtuális. Mindket esetben a t tárgytávolság jóval nagyobb, mint az f fókusztávolság (ami a két esetben azonos), tehát a képtávolság k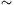f. Mivel t is, k is azonos a két esetben, a kép mérete is az.

P. 3414. A paksi atomerőműben az 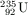atommag egy ,,termikus'' neutronnal ütközve 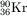-ra és 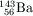-ra hasadhat, miközben három gyors neutron is keletkezik. A Kr és a Ba izotóp instabil, 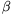-sugárzást kibocsátva még négyszer bomlanak. Mik a végtermékek? (4 pont)

Közli: Korpássy Péter, Budapest

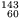Megoldás. ${\phantom1}{}^{90}_{40}$ Zr (cirkónium) és ${}^{143}_{\phantom{1}60}$ Nd (neodínium)

P. 3415. Egy hagyományos lemezjátszót 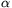szögben megdöntünk. Ráteszünk a korongjára egy kis testet, a tengelyétől r távolságra, a lehető legalacsonyabb helyzetben. Ezután a korongot nyugalmi helyzetből indítva 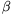szöggyorsulással forgatjuk. A kis test t idő múlva csúszik meg.

a) Mekkora a 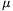tapadási súrlódási együttható a korong és a kis test között?

b) Legalább mekkora legyen 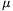, hogy kezdetben még ne csússzon meg a test? (6 pont)

Közli: Balogh Péter, Budapest

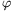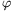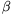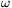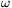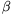Megoldás. Jelölje phi (t) a korong elfordulását ( phi (t)= beta t²/2), a pillanatnyi szögsebességét pedig omega (t) ( omega (t)= beta t). A testet mgcos 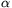alpha erő nyomja a koronghoz, és mgsin 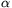alpha erő próbálja az esésvonal mentén lehúzni. Ezen kívül hat még a súrlódási erő, melynek a nagysága pont akkora, hogy az összes erő eredőjének radiális komponense -m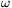²(t)r, a tangenciális komponens pedig m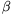r:

$S_t(t)-mg\sin\alpha\sin\varphi(t)=mr\beta\,,$

$S_r(t)+mg\sin\alpha\cos\varphi(t)=-m\omega^2(t)r\,.$

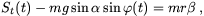
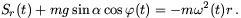
Innen

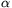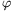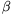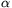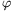S²(t)=(mgsin alpha sin phi (t)+mr)²+(mgsin alpha cos phi (t)+m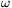²(t)r)²

adódik.

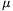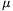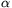a) A tapadási súrlódási együtthatót az S(t)=mgcos alpha egyenlet adja meg.

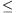
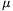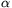b) A kis test akkor nem csúszik meg rögtön az indításkor, ha S(0)mgcos alpha , azaz

$\sqrt{\left({r\beta\over g\cos\alpha}\right)^2+{\rm tg}^2\alpha}\leq\mu.$

Már regisztráltál?
Új vendég vagy?