A 2001. áprilisi C-jelű matematika feladatok megoldása
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
C. 625. A McDonald's éttermekben 6-os, 9-es vagy 20-as csomagolásban rendelhetünk Chicken McNuggets-et. (Így például kérhetünk 21 darabot, mert 21=6+6+9, de semmilyen módon nem kaphatunk 19 darabot.) Melyik az a legnagyobb darabszám, amit nem tudunk rendelni?
Megoldás. Ha találunk hat egymást követő pozitív egész számot, amely felbontható a 6, 9 és a 20 összegére, akkor újabb 6-osok hozzáadásával az összes ennél nagyobb pozitív egész is előállítható ezen a módon. Könnyen meggyőződhetünk róla, hogy a 43 nem áll elő ezen számok összegeként, viszont
44=20+6+6+6+6
45=9+9+9+9+9
46=20+20+6
47=20+6+6+6+9
48=6+6+9+9+9+9
49=20+20+9.
Így 44-től kezdve bármelyik egész szám előáll a kívánt módon, tehát a 43 az a legnagyobb darabszám, amit nem áll módunkban megrendelni.
C. 626. Az 5 egység sugarú körlapot vágjuk szét két húrral három egyenlő területű részre. Milyen hosszúak ezek a húrok?
Javasolta: Reményi Gusztáv, Budapest
Megoldás.
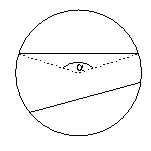
A területek egyenlőségéből következik, hogy a húrok által levágott két körszelet területe a kör területének harmadrésze, tehát \(\displaystyle {1\over3}r^2\pi={1\over2}r^2(\overset\frown\to\alpha-\sin\alpha)\), amiből \(\displaystyle \sin\alpha=\overset\frown\to\alpha-{2\over3}\pi\). A két oldalt ábrázolva látható, hogy az egyenletnek egyetlen megoldása van,
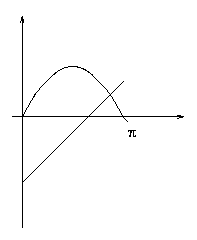
méghozzá \(\displaystyle {2\over3}\pi\) és \(\displaystyle pi\) között, tehát a megoldást x-szel jelölve 2,09<x<3,15. Helyettesítsünk be először (próbaképpen) 2,5-et. Erre az értékre azt kapjuk, hogy \(\displaystyle \sin2,5=0,597\)0,406=2,5-{2\over3\pi}">,
tehát x>2,5. \(\displaystyle alpha\)=2,7-re 0,4272<0,606, tehát x<2,7. \(\displaystyle alpha\)=2,6-re 0,515>0,506, ami már kisebb különbség, így próbálkozzunk most \(\displaystyle alpha\)=2,61-gyel. Erre az értékre 0,506<0,516 jön ki, tehát 2,6<x<2,61. Legyen most \(\displaystyle alpha\)=2,605. Ekkor sin2,605=0,511 és \(\displaystyle 2,605-{2\over3}\pi=0,511\), tehát három tizedesjegy pontossággal azt kapjuk, hogy a keresett gyök 2,605. Tehát x=2,605, amiből a két húr hossza \(\displaystyle 5\cdot2\sin{{\alpha}\over2}=9,664\).
C. 627. Oldjuk meg a következő egyenletrendszert:
a+b=c+d,
a3+b3=c3+d3.
Javasolta: Ábrány Miklós, Beregszász
Megoldás. (a+b)3=a3+b3+3ab(a+b)=c3+d3+3ab(c+d), (a+b)3=(c+d)3=c3+d3+3cd(c+d).
Ebből ab=cd vagy c+d=0. Utóbbi esetben a+b=0, ekkor a=-b, c=-d megoldásai az egyenletrendszernek. Ha ab=cd, akkor a+b=c+d felhasználásával (a+b)2-2ab=(c+d)2-2cd, és ebből (a-b)2=(c-d)2. Két eset van. Az első: a-b=c-d. Mivel a+b=c+d, ebből a=c és b=d következik. A második eset: a-b=d-c. Ebből a=d, b=c. Tehát az egyenletrendszernek összesen három esetben van megoldása, mindegyikben végtelen sok:
I. a=c, b=d
II. a=d, b=c
III. a=-b, c=-d.
C. 628. Egy tetraéder alakú kartondobozt felvágunk az egyik csúcsából induló három éle mentén, majd az ,,elváló'' lapokat leterítjük a fenti csúccsal szemközti lap síkjába. Így egy 30 cm oldalú négyzetet kapunk. Mekkora a tetraéder térfogata?
Megoldás. Az m=30 cm oldalú negyzet lesz a tetraéder testhálója. Belátható, hogy a hálóról hiányzó szakaszok csak a rajzon látható módon (pirossal jelöltük) helyezkedhetnek el. Legyen az alaplap a T területű derékszögű háromszög, ekkor \(\displaystyle T={{a^2}\over2}={{15^2}\over2}=112,5\) \(\displaystyle ({\text cm}^2)\).
A tetraéder magassága az m=30 cm lesz, így \(\displaystyle V={{T\cdot m}\over3}=1125\) \(\displaystyle ({\text cm}^3)\).
C. 629. Igazoljuk, hogy ha tizenhárom egész szám összege osztható 6-tal, akkor a tizenhárom szám tizenharmadik hatványának összege is osztható 6-tal.
Javasolta: Székelyhidi Tamás, Ercsi
Megoldás. Legyen a egy egész szám, ekkor 6|a13-a, hiszen a13-a=a(a6-1)(a6+1)=a(a-1)(a+1)(a4+a2+1)(a6+1).
Az első három tényező szorzata biztosan osztható 6-tal. Ez azt jelenti, hogy a13 és a 6-tal osztva ugyanannyi maradékot ad. Így ha a tizenhárom egész szám összege osztható volt 6-tal, akkor a tizenhárom egész szám tizenharmadik hatványának összege is osztható 6-tal.

