 |
Exercises and problems in Physics |
Please read The Conditions of the Problem Solving Competition.
New experimental problem:
M. 224. Determine, applying dripping or some other method, the proportion of the surface tension of eau de cologne to that of water. (6 points)
New problems:
P. 3426. One of two trains travelling on parallel tracks covers 90 km per hour, the other one 10 meters per second. A passenger travelling in one of the trains sees the other train pass by is 8 seconds. What is the length of the other train? (3 points)
P. 3427. An airliner takes off from the runway at a speed of 190 km/h, and reaches a height of 2000 m and a speed of 540 km/h in 40 seconds, following a straight trajectory with a uniform acceleration. a) During the rise, what are the magnitude and the direction of the acceleration of the plane? b) During the rise, the suitcase on the floor of the plane does not slip. What is the minimum coefficient of static friction required for this? (Assume that the plane of the floor is parallel to the velocity.) (4 points)
P. 3428. A small axle is fastened to one end of a thin staff of mass m, perpendicular to the staff. The axle can slide without friction on the horizontal track shown in the figure. The staff tumbles over to one side from its unstable equilibrium position. a) Will the force exerted onto the track ever be zero? b) Will the axle of the staff ever lose touch with the track? c) What is the force pressing the track when the staff has turned 0o, 90o and 180o?
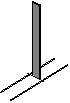
(5 points)
P. 3429. A table-tennis player moves his bat up and down in such a way that the ball always bounces to a height of 40 cm from the bat. The collision number is 0.5. What is the speed of the bat when hitting the ball? (The mass of the ball is much less than that of the bat and air resistance is also negligible.) (4 points)
P. 3430. A sun furnace has been at work in the Pyrenees since 1969, in which 63 mirrors of 30 m2 each reflect the sunlight into a small area. How much energy do the mirrors at least concentrate if a hole with a diameter of 15 cm can be melted in 1 minute into a 1 cm thick iron plate with an initial temperature of 35 oC? What is at least the power output of the sun furnace? (3 points)
P. 3431. There is some water at
T0=80 oC in a tub, the temperature of the
surroundings is T*=20 oC. The temperature of
the water as a function of time goes as follows:
T(t)=T*+(T0-T*)e-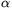
t, where 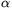is a constant characteristic of
the cooling. During the first 5 minutes, the temperature decreases by
10 oC. How much later should the same amount of water of
10 oC be poured again into the tub so that the mixture reaches
the temperature of 30 oC as soon as possible? (5 points)
P. 3432. Identical metal spheres are placed into the vertices of a regular tetrahedron. The spheres do not touch. When a single sphere (A) is given a charge of 20 nC it reaches the same potential as when A and another sphere are given 15 nC each. What equal charges should be given to A and to two other spheres, and what equal charges to all four spheres so that the potential of sphere A is always the same? (6 points)
P. 3433. An old voltmeter reads the voltage of a battery as 0.7 V at a measuring limit of 1 V, and as 2.6 V at a measuring limit of 10 V. What does the voltmeter read at a measuring limit of 100 V? (4 points)
P. 3434. Determine the resultant resistance of the infinite circuit made up of 1 k\(\displaystyle Omega\) resistors shown in the figure between points A and C, and between points A and B.
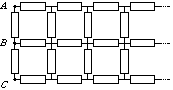
(6 points)
P. 3435. A coil with an inductivity of 0.2 H and an ohmic resistance of 62.8 \(\displaystyle Omega\) is connected to the mains alternating voltage. a) What should the capacity of the capacitor connected in series with the coil be so that the active power does not change? b) Can the power factor be improved by connecting a capacitor parallel to the coil? Can the power factor be increased to 1? (4 points)
P. 3436. One of the planets of star Noname is long and cylindrical. The average density of the planet is identical to that of the Earth, its radius equals that of the Earth and the period of its revolution is exactly 1 day. a) What is the first cosmic speed for this planet? b) How high above the surface of the planet do the synchronous telecommunications satellites orbit? c) What is the second cosmic speed for this planet?
(5 points)
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.