New exercises and problems in Mathematics
April
2001
Please read The Conditions of the Problem Solving Competition.
 |
New exercises in April 2001 |
C. 625. At McDonald's you can order Chicken McNuggets in boxes of 6, 9, and 20. What is the largest number of nuggets that you cannot get no matter what combination of the above boxes you order?
C. 626. Two chords of a disc of radius 5 divide the disc into three parts of equal areas. How long are these chords?
Proposed by G. Reményi, Budapest
C. 627. Solve the following system of equations: a+b=c+d, a3+b3=c3+d3.
Proposed by M. Ábrány Beregszász
C. 628. A tetrahedron shaped cardboard box is `cut open' along three edges starting at the same vertex and is developed in the plane where its four faces form a square with 30 cm long sides. Determine the volume of the tetrahedron.
C. 629. Thirteen integers add up to a number divisible by 6. Prove that their thirteenth powers also add up to a multiple of 6.
Proposed by T. Székelyhidi, Ercsi
 |
New problems in April 2001 |
B. 3452. Two players alternately mark the fields of a 5x5 board. The one who moves first always writes one X sign, while the second player always writes two O signs. The one who first completes a row or a column of the board with her signs, wins the game. How can the second player win the game? (4 points)
Proposed by N. Gyanta, Budapest
B. 3453. In a triangle ABC whose centroid is denoted by S, points H and Q are the midpoints of segments AS and AB, respectively. The line parallel to BC through H intersects the segment AB at P and the line CQ at R. Find the ratio between the areas of triangles PQR and APH. (3 points)
Proposed by T. Káspári, Paks
B. 3454. We have 27 unit cubes. a) Is it possible to paint the faces of these small cubes with three colours: purple, white and yellow, in such a way that they can be arranged, in three different ways, three cubes, each of edge-length 3, whose whole surface is purple, white, and yellow, respectively? b) Find the smallest number such that no matter how one paints this many faces of the small cubes with purple, it is possible to form a cube of edge-length 3 whose complete surface is purple. (4 points)
B. 3455. Find infinitely many pairs of integers (m, n) such that the numbers m and n have the same prime divisors, and also m+1 and n+1 have identical prime factors. (5 points)
Proposed by N. Gyanta, Budapest
B. 3456. Each edge of a tetrahedron is labelled by a positive integer. We may change these numbers such that at each time we choose one vertex of the tetrahedron and replace the three numbers assigned to the edges starting at that vertex as follows: To each edge we write either the sum or the difference of the numbers written on the other two edges, writing the sum in one case and the difference in the other two cases. When we write the difference of the numbers a and b we may freely choose either a-b or b-a. Is it possible to achieve, iterating this procedure a finite number of times, that 0 is written on every edge of the tetrahedron in the end? (3 points)
Proposed by J. Mezei, Vác
B. 3457. Determine those positive prime numbers p and q for which the equation x4+p2x+q=0 has a repeated root. (4 points)
Proposed by Á. Besenyei, Budapest
B. 3458. In the plane n red points are given. Prove that it is possible to place 2n blue points such that each triangle formed by the red points contains at least a blue one in its interior. (5 points)
B. 3459. Circles of radii a, b, c, d that lie outside each other are drawn around the consecutive vertices A, B, C, D of a parallelogram such that a+c=b+d. Prove that the four lines obtained as common external tangents to opposite circles form a circumscribed quadrilateral. (4 points)
B. 3460. In a triangle, the point where the incircle
touches the side opposite to the angle \(\displaystyle gamma\) divides the side into segments whose lengths are x and
y. Prove that the area of the triangle is equal to 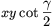 . (4
points)
. (4
points)
Proposed by Á. Besenyei, Budapest
B. 3461. Let a>0 and c\(\displaystyle ne\)0 be integers. Prove that if the Diophantine equation x2-ay2=c has at least 4c2+1 different solutions, then it has infinitely many solutions. (5 points)
Proposed by E. Fried, Budapest
 |
New advanced problems in April 2001 |
A. 263. On a circle there are n red and n blue arcs given in such a way that each red arc intersects each blue one. Prove that some point is contained by at least n of the given coloured arcs.
Schweitzer Competition, 2000
A. 264. The rational numbers in the interval (0,1) are mapped, by a polynomial p of real coefficients, onto the set of all rational numbers of an other interval. Prove that the degree of p is not greater than 1.
Proposed by E. Fried, Budapest
A. 265. A sequence a1,
a2, ... is defined recursively as follows. Let
a1=a2=a3=1 and 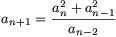 for n\(\displaystyle ge\)3. Prove
that each term of the sequence is an integer.
for n\(\displaystyle ge\)3. Prove
that each term of the sequence is an integer.
Send your solutions to the following address:
KöMaL Szerkesztőség (KöMaL feladatok), Budapest Pf. 47. 1255, Hungary
or by e-mail to: solutions@komal.elte.hu.
