A 2001. májusi C-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 630. Egy négyjegyű szám első két számjegyének összege egyenlő az utolsó két számjegy összegével. Az első és az utolsó számjegy összege a harmadik számjegyet adja. A második és negyedik számjegy összege az első és a harmadik összegének kétszerese. Melyik ez a négyjegyű szám?

Megoldás. Legyen a négyjegyű szám \(\displaystyle \overline{abcd}\). Tudjuk, hogy a+b=c+d, a+d=c, b+d=2(a+c). Az első és a harmadik egyenletben c helyére a+d írható, a rendezés után ezt a két egyenletet kapjuk: b=2d, b=4a+d, amiből 4a=d. Az a lehetséges értékei 1, 2. Ha a=1, akkor d=4, b=8, c=5, vagyis a négyjegyű szám 1854.

Ha a=2, akkor d=8, de ekkor b már nem számjegy. Tehát az egyetlen megoldás 1854.

C. 631. Az y=|x-1|+|x+1| függvény grafikonja és az y=c egyenletű egyenes által közrezárt síkidom területe 30. Mekkora a c állandó értéke?

Megoldás. Ábrázoljuk először az y=|x-1|+|x+1| függvényt. Három eset van:

1. x<-1, ekkor a függvény y=-x+1-x-1=-2x;

2. \(\displaystyle -1\leq x<1\), ekkor y=-x+1+x+1=2;

3. \(\displaystyle 1\leq x\), ekkor y=2x.

Tehát a függvény:

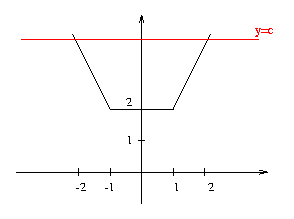
A függvény és az y=c egyenes által határolt síkidom egy trapéz,

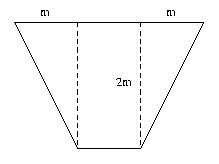
melynek területe \(\displaystyle t={{(4+2m)\cdot2m}\over2}=2m^2+4m=30\), amiből m=-5 vagy m=3 adódik. Ebből csak a második jó megoldás. Tehát c=2+2m=8.

C. 632. A 3, 15, 24, 48, ... sorozat a 3 azon többszöröseiből áll, amelyek 1-gyel kisebbek egy négyzetszámnál. Mennyi a maradék, ha a sorozat 2001-edik tagját elosztjuk 1000-rel?

Javasolta: Magyar Zsolt, Budapest

Megoldás. Mivel csak a 3k\(\displaystyle pm\)1 alakú számok négyzete ad 3-mal osztva 1-et maradékul, ezért három egymást követő négyzetszámból kettő a sorozathoz tartozik. Vagyis 3000 darab egymást követő négyzetszám esetén van 2000 tagja a kérdéses sorozatnak. Most az első négyzetszám a 2², mert ehhez tartozik a 2²-1=3. A 3000. négyzetszám a 3001², ehhez tartozik a 3001²-1, ami a sorozat 2000. tagja. A 3002²-1 lesz a 2001. tag, ami 9012003, vagyis 1000-rel osztva 3 a maradék.

C. 633. Egy tetraéder lapjainak területe egyenlő, továbbá a háromszög lapok beírható köreinek sugarai is egyenlőek. Mutassuk meg, hogy a tetraéder lapjai egybevágóak.

Megoldás.

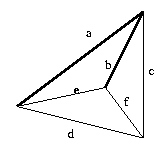
Mivel a területek és a beírt körök sugara egyenlő, ezért t=rk/2 miatt a háromszögek kerülete is egyenlő. Legyen a kerület k, ekkor 2(a+b+c+d+e+f)=2(2k). Mivel d+e+f=k, ezért a+b+c=k, vagyis az egy csúcsból induló élek összege is k. Így beláttuk, hogy az a+b összeget az e és a c is k-ra egészíti ki, amiből e=c következik. Hasonlóan igaz b=d, valamint a=f. Ez pedig igazolja az egybevágóságot.

C. 634. Csonkakúp alakú, felfelé szélesedő 1 literes háztartási mérőedényen a 1/2 liter jele az edény magasságának 2/3 részénél található. Mekkora az alapkör és a fedőkör átmérőjének aránya?

Megoldás.

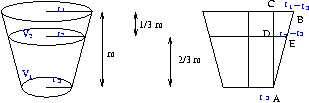
\(\displaystyle AED\triangle\sim ACB\triangle\), így \(\displaystyle {{r_2-r_3}\over{r_1-r_3}}={{{2\over3}m}\over m}\), és ebből \(\displaystyle r_2={2\over3}r_1+{1\over3}r_3\). Mivel V₁=V₂, ezért \(\displaystyle {{\pi}\over3}\cdot{2\over3}m((r_2)^2+(r_3)^2+r_2r_3)={{\pi}\over3}\cdot{1\over3}m((r_2)^2+(r_1)^2+r_2r_1)\). Ebbe behelyettesítve az r₂-re fent kapott kifejezést, majd átrendezve kapjuk, hogy 0=25r₃²+13r₁r₃-11r₁². Ebből \(\displaystyle 0=25\left({{r_3}\over{r_1}}\right)^2+13\left({{r_3}\over{r_1}}\right)-11\), amiből \(\displaystyle {{r_3}\over{r_1}}={{-13\pm\sqrt{1269}}\over{50}}\), aminek egyetlen pozitív gyöke a 0,452. Tehát az alapkör és a fedőkör átmérőjének az aránya 0,452.