Matematikából kitűzött gyakorlatok és feladatok
2001. november

B. 3492. Egy nxn-es táblázatba beírjuk sorban az 1, 2, ..., n² számokat:

Minden sorból kiválasztunk egy-egy számot úgy, hogy semelyik kettő ne legyen ugyanabban az oszlopban.

Mik a kiválasztott számok összegének lehetséges értékei? (3 pont)

IMC 8, Prága, 2001

B. 3493. Ketten a következő játékot játsszák. Egy kupacból, amelyben kezdetben páratlan darab gyufaszál van, felváltva vesznek el minden lépésben egy, két vagy három szál gyufát, amíg mind el nem fogy. Az nyer, akinél a végén páros számú gyufa van.

A kezdőnek, vagy ellenfelének van-e nyerő stratégiája? (5 pont)

Kvant

B. 3494. Igazoljuk, hogy ha az ax³+bx²+cx+d=0 egyenletnek három különböző pozitív gyöke van, akkor bc<3ad. (4 pont)

Javasolta: Bakonyi Gábor, Budapest

B. 3495. Az ABCD téglalap oldalai AB=3, BC=2. P az AB oldalnak az a pontja, amelyre a PD egyenes érinti, mégpedig E-ben, a BC átmérőjű kört. A kör középpontján és E-n átmenő egyenes az AB oldalt Q-ban metszi. Mekkora a PQE háromszög területe? (3 pont)

Javasolta: Gerőcs László, Budapest

B. 3496. Az ABCD négyzet belsejében úgy vettük föl a P pontot, hogy AP:BP:CP=1:2:3. Mekkora az APB szög? (4 pont)

B. 3497. Az x valós számra {x}+{x^-1}=1. Határozzuk meg

{x²⁰⁰¹}+{x^-2001}

értékét. (4 pont)

Javasolta: Besenyei Ádám, Tatabánya

B. 3498. Az ABC háromszögben C-nél derékszög van. A hegyesszögek szögfelezői a szemközti oldalakat az M és az N pontban metszik. Legyen P az MN szakasz és a C-ből induló magasság metszéspontja. Bizonyítsuk be, hogy a CP hossza egyenlő a beírt kör sugarával. (4 pont)

Javasolta: Merényi Imre, Budapest

B. 3499. Az x és y pozitív számok mértani közepe g. Bizonyítsuk be, hogy ha g3, akkor 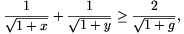ha pedig g2, akkor \(\displaystyle {1\over\sqrt{1+x}}+{1\over\sqrt{1+y}}\leq{2\over\sqrt{1+g}}\). (5 pont)

B. 3500. Száz fiú és száz lány áll egy-egy sorban egymással szemben. Minden egyes fiú kiválaszt magának egy lányt (ugyanazt a lányt többen is választhatják) és egyenesen odamegy hozzá. Útközben a fiúk útvonalai nem keresztezik egymást. Ezután a fiúk visszaállnak a helyükre, most a lányok választanak, és most is teljesül, hogy miközben egyenesen odamennek a kiszemelt fiúhoz, az útvonalaik nem keresztezik egymást. Bizonyítsuk be, hogy van olyan lány és fiú, akik egymást választották. (4 pont)

B. 3501. Adottak a térbeli koordinátarendszerben az A(1, 1, 1) és a P(1, 1, 0) pontok. Forgassuk el az OA félegyenes körül pozitív irányban 60^o-os szöggel a P pontot. Határozzuk meg az elforgatott pont koordinátáit. (4 pont)

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 275. Egy nxn-es táblázatba beírjuk sorban az 1², 2², 3², ..., (n²)² számokat:

Minden sorból kiválasztunk egy-egy számot úgy, hogy semelyik kettő ne legyen ugyanabban az oszlopban.

Mik a kiválasztott számok összegének lehetséges értékei?

Terpai Tamás ötletéből

A. 276. Az x₁, ..., x_n pozitív számok szorzata 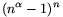, ahol 1 valós szám. Bizonyítsuk be, hogy

\(\displaystyle \sum_{i=1}^n{1\over(x_i+1)^{1/\alpha}}\ge1.\)

A. 277. Legyen H₁ egy n-oldalú sokszög. Készítsük el a H₁, H₂, ..., H_n sokszögsorozatot a következőképpen. Ha H_k-t már elkészítettük, akkor H_k+1-et úgy kapjuk, hogy H_k csúcsait rendre tükrözzük a pozitív körüljárás szerinti k-adik szomszédjukra.

Bizonyítsuk be, hogy ha n prímszám, akkor a H₁ és H_n sokszögek hasonlók.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518