A 2002. márciusi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3532.Egy csodabogár a négyzethálós papírlapon sétál. Egy lépéssel jobbra mindig két mezőt, balra négyet, felfelé hármat, lefelé pedig ötöt tud lépni. Sétája során minden egyes lépés után pontosan 90^o-kal fordul el. Melyek azok a mezők, ahova a bogár sétája során eljut?

(3 pont)

Megoldás. Úgy is képzelhetjük, hogy a bogár a végtelen négyzetrács rácspontjain sétál a leírt feltételekkel. Vegyünk fel egy koordinátarendszert, melynek origója a bogár kiindulási pontja, tengelyei pedig párhuzamosak a rácsot meghatározó vízszintes és függőleges egyenesekkel. Akár jobbra, balra, felfelé vagy lefelé lép, a bogár helyzetének első koordinátája páros számmal változik meg. Ezért a bogár csak olyan rácspontokba juthat el, melyek abszcisszája páros szám. A továbbiakban megmutatjuk, hogy minden ilyen rácspontra el tud jutni a bogár.

Olyan sétákat fogunk tekinteni, nevezzük ezeket megengedett sétáknak, melyek vízszintes lépéssel kezdődnek és függőleges lépéssel fejeződnek be; ilyen sétákból aztán tetszőleges sorozatot készíthetünk úgy, hogy az egyik séta végpontja lesz a következő séta kezdőpontja. A jobbra-föl séta eredményeként a bogár a (2,3) vektorral mozdul el, n ilyen séta egymásutánjával tehát a (2n,3n) pontba jut el. A jobbra-föl-balra-le séta eredményeként a bogár a (-2,-2) vektorral mozdul el, n ilyen séta egymásutánjával pedig a (-2n,-2n) pontba jut el. Minden N páros számra van tehát olyan megengedett séta, melynek során a bogár egy N abszcisszájú pontba jut el.

Most már csak azt kell megmutatni, hogy ha a bogár egy megengedett sétával eljutott valamelyik föggőleges rácsegyenesre, akkor annak bármelyik rácspontjába is el tud jutni. Világos, hogy ehhez elég egy-egy olyan megengedett sétát mutatni, melynek során a bogár a (0,1) illetve a (0,-1) vektorral mozdul el. Az elsőhöz tekintsük a jobbra-fel-jobbra-fel-balra-le sétát. A másodikhoz először tekintsük a jobbra-fel-jobbra-le-balra-le sétát, ennek során a bogár a (0,-7) vektorral mozdul el, majd illesszük ez után hatszor azt a sétát, melynek segítségével a bogár a (0,1) vektorral mozdul el.

B.3533. Anna egy nagy rajzlapra felírt 32 egész számot és mindegyiket letakarta egy-egy kártyalappal. Ezután odahívta Balázst azzal, hogy ha kiválaszt 7 lapot, akkor elárulja neki, hogy az alattuk lévő számok összege páros-e vagy páratlan. Legalább hányszor kell Balázsnak választania, ha meg akarja tudni, hogy a rajzlapra felírt 32 szám összege páros vagy páratlan? (4 pont)

Megoldás. Először megmutatjuk, hogy 6 kérdés elegendő. Vegyük észre, hogy néhány szám összege pontosan akkor páros, ha a 2-vel való osztás során kapott maradékaik összege páros. Válassza ki Balázs az első 7 számot letakaró 7 lapot, a második 7 számot letakaró 7 lapot, a harmadik 7 számot letakaró 7 lapot, a negyedik 7 számot letakaró 7 lapot, az első 5 számot és még a 29. és a 30. számot letakaró 7 lapot, végül pedig az első 5 számot és még a 31. és a 32. számot letakaró lapokat. Ha valamely 7 lap alatt talalható számok s_i összege páros, akkor írjon le egy 0-t, ha páratlan, akkor egy 1-est. Ha a leírt 6 szám öszege páros, akkor a 32 szám összege is páros, ellenkező esetben pedig páratlan. Valóban, az s_i számok összege megegyezik azzal a számmal, amit úgy kapunk, hogy a 32 szám összegéhez hozzádjuk az első 5 szám összegének kétszeresét. A 32 szám összege tehát pontosan akkor páros, ha az s_i számok összege páros. Fenti megjegyzésünk alapján pedig ez pontosan akkor teljesül, ha a Balázs által lejegyzett 6 szám összege páros.

Most megmutatjuk, hogy 5, vagy annál kevesebb kérdés nem elegendő. 4, vagy annál kevesebb kérdés nem elegendő, hiszen akkor lesz olyan szám, amely egyáltalán nem szerepel a Balázs által kiválasztott lapok között. Ha ezek közül az egyik helyére eggyel nagyobb számot képzelnénk, ugyanazokat a válaszokat kapnánk, miközben a 32 szám összegének paritása megváltozna. Ugyanilyen okok miatt 5 kérdés is csak akkor bizonyulhatna elegendőnek, ha az ötször 7 lekérdezett kártyalap az összes számot takarja. Ekkor a következő lehetőségekkel kell számolnunk:   (a) valamelyik kártyalap 4 kérdésben is szerepelt (az összes többi pedig pontosan egy kérdésben);   (b) egyik lap 3 kérdésben, egy másik pedig 2 kérdésben;   (c) három különböző kártyalap szerepelt 2 kérdésben. A (b) és (c) esetben legyen A egy olyan szám amely(et letakaró kartyalap) pontosan 2 kérdésben szerepelt, továbbá legyen B és C egy-egy olyan szám, amely a 2 kérdésben A mellett szerepelt, de amelyekre csak egyszer kérdezett rá Balázs. Képzeljük az A,B,C számok helyére rendre az A+1,B-1,C-1 számokat, a többi számot változatlanul hagyva. Ekkor a 32 szám összege eggyel csökken, tehát paritása megváltozik, ellenben Balázs mind az 5 kérdésére Anna ugyanazt a választ adná. Így ezzel az 5 kérdéssel nem lehet megtudni, hogy a számok összege páros-e avagy páratlan. Az (a) esetben legyen A az a szám, amelyik 4 kérdésben is szerepelt, B,C,D,E pedig egy-egy olyan szám, amely a 4 kérdésben A mellett szerepelt. Ha most az A,B,C,D,E számok helyére rendre az A+1,B-1,C-1,D-1,E-1 számokat képzeljük, a többi számot változatlanul hagyva, akkor a 32 szám összege most 3-mal csökken, tehát paritása ismétcsak megváltozik, ellenben Balázs mind az 5 kérdésére Anna ebben az esetben is ugyanazt a választ adná. Így ezzel az 5 kérdéssel sem lehet megtudni, hogy a számok összege páros-e avagy páratlan.

B.3534. A futballpályán egy támadás során a csatár olyan törött vonal mentén futott, amelyet minden, a pálya valamelyik oldalával párhuzamos egyenes legfeljebb egyszer metsz. Igazoljuk, hogy a csatár nem futhatott többet a pálya két szomszédos oldalának összegénél. (3 pont)

Megoldás. Vegyünk fel egy olyan koordinátarendszert, melynek origója a csatár útvonalának P₀ kezdőpontja, tengelyei pedig párhuzamosak a pálya oldalaival. A tengelyek irányítását válasszuk meg úgy, hogy a csatár útvonala az I. síknegyedbe essen. Ha a csatár útvonala a P₀P₁...P_n töröttvonal, akkor legyenek a P_i pont koordinátái x_i és y_i. A feltétel miatt 0=x₀$\displaystyle le$x₁$\displaystyle le$...$\displaystyle le$x_n$\displaystyle le$a és 0=y₀$\displaystyle le$x₁$\displaystyle le$...$\displaystyle le$y_n$\displaystyle le$b, ahol a és b a pálya két szomszédos oldalának hossza. A háromszög egyenlőtlenség miatt a P_iP_i+1 szakasz d_i hosszára d_i$\displaystyle le$(x_i+1-x_i)+(y_i+1-y_i), ahol egyenlőség pontosan akkor áll fenn, ha x_i+1=x_i vagy y_i+1=y_i. A csatár útvonalának hossza $\displaystyle \sum_{i=0}^{n-1}d_i\le\sum_{i=0}^{n-1}\Bigl((x_{i+1}-x_i)+(y_{i+1}-y_i)\Bigr)=\sum_{i=0}^{n-1}(x_{i+1}-x_i)+\sum_{i=0}^{n-1}(y_{i+1}-y_i)=x_n+y_n\le a+b\ ,$ ahogy azt bizonyítani kellett. Az is leolvasható a megoldásból, hogy egyenlőség akkor és csak akkor állhat fent, ha a csatár a pálya egyik sarkából indult, útját a pálya átellenes sarkában fejezte be, és állandóan a pálya valamelyik oldalával párhuzamosan futott.

B.3535. Bizonyítsuk be, hogy az ABC háromszög BC, CA és AB oldalegyenesein lévő U, V, W pontokban az oldalakra állított merőlegesek pontosan akkor mennek át egy ponton, ha

AW²+BU²+CV²=AV²+CU²+BW².

(3 pont)

Megoldás. Tegyük fel először, hogy a három egyenes a P pontban metszi egymást, és vezessük be az s=UP²+VP²+WP² mennyiséget. A Pithagorasz tétel alapján AW²+BU²+CV²+s=AP²+BP²+CP²=AV²+CU²+BW²+s, ahonnan a bizonyítandó egyenlőség azonnal leolvasható.

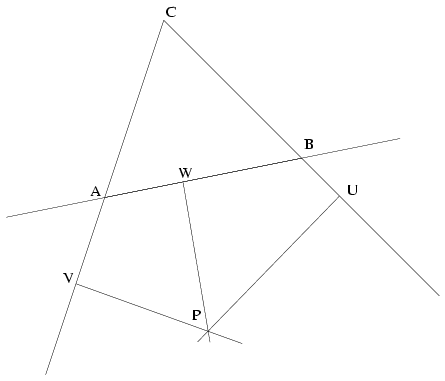
Tegyük fel most, hogy a három egyenes nem megy át egy ponton, és legyen Q az U és V pontokban a megfelelő oldalegyenesekre állított merőlegesek metszéspontja. Jelöljük a Q pontból az AB oldal egyenesére állított merőleges talppontját W₀-val, ekkor W₀$\displaystyle ne$W. Az első rész alapján AW₀²+BU²+CV²=AV²+CU²+BW₀² vagyis (AW₀-BW₀)(AW₀+BW₀)=AV²+CU²-BU²-CV². A már bizonyított állítás megfordításának igazolásához elég annyit megmutatni, hogy (AX-BX)(AX+BX)$\displaystyle ne$(AY-BY)(AY+BY) ha X,Y az AB egyenes két különböző pontja.

Ezt a következőképpen tehetjük meg. Az (AX-BX)(AX+BX) kifejezés értéke pontosan akkor 0, ha X az AB szakasz F felezőpontja, és attól függően vesz fel pozitív vagy negatív értéket, hogy X az FB vagy az FA nyílt félegyenesen helyezkedik-e el. Szimmetria okok miatt feltehetjük tehát, hogy X és Y is az FB félegyenesen helyezkedik el. Mozgassuk az X pontot F-ből indulva az FB félegyenesen, folyamatosan távolodva az F ponttól. Kezdetben az x=(AX-BX)(AX+BX) kifejezés értéke 0, és amíg X az FB szakaszon mozog, addig AX szigorúan nő, BX szigorúan csökken, AX+BX pedig változatlan; ennek megfelelően x értéke szigorúan növekedő. A B pontot elérve, és azon túl pedig AX-BX értéke marad változatlan, míg AX és BX is szigorúan növekedő lesz; x értéke tehát ebben az intervallumban is szigorúan nő. Ezért ha X és Y is az FB félegyenes pontja, akkor az (AX-BX)(AX+BX)=(AY-BY)(AY+BY) egyenlőségből X=Y következik, amit igazolni akartunk.

B.3536. Határozzuk meg

$\displaystyle {x^2\over8}+x\cos x+\cos2x$

legkisebb értékét. (4 pont)

Megoldás.

$\displaystyle {x^2\over8}+x\cos x+\cos2x={x^2\over8}+x\cos x+2\cos^2x-1={1\over8}(x+4\cos x)^2-1\ge-1\ ,$

és egyenlőség pontosan akkor áll fenn, ha f(x)=x+4cosx=0. Az f folytonos függvény értéke az x=0 helyen f(0)=4, vagyis pozitív, míg az x=$\displaystyle pi$ helyen f($\displaystyle pi$)=$\displaystyle pi$-4, vagyis negatív. Ezért (Bolzano tétele miatt) van olyan 0<x<$\displaystyle pi$ hely, ahol f(x)=0. A feladatban szereplő kifejezés legkisebb értéke tehát -1.

B.3537. Az ABC háromszög AC oldala a B-ből induló szögfelezőt D-ben, a B-ből induló magasságot H-ban metszi, a beírt kört pedig E-ben érinti. Az AC felezőpontja F. Bizonyítsuk be, hogy az EF szakasz az FD és FH szakaszok mértani közepe. (4 pont)

Megoldás. Jelölje a háromszög oldalait a szokásos módon a,b és c. Ha a=c, akkor a D,E,F és H pontok egybeesnek, ebben az esetben az állítás nyilván igaz. Egyébként pedig az általánosság megszorítása nélkül feltehetjük, hogy a>c, ekkor a C,F,D,E,H pontok ebben a sorrendben követik egymást a CA félegyenesen. Az EF, FD és FH szakaszok meghatározásához számoljuk ki előbb a CD, CE, CF és CH szakaszok hosszát. Nyilván CF=b/2 és CE=s-c=(a+b-c)/2, ahonnan EF=CE-CF=(a-c)/2. A szögfelező tétel alapján $\displaystyle CD={a\over a+c}b$, ezért $\displaystyle FD=CD-CF=b{a-c\over2(a+c)}$. Végül a koszinusz tételt felhasználva kapjuk, hogy CH=acos$\displaystyle gamma$=(a²+b²-c²)/2b, vagyis FH=CH-CF=(a²-c²)/2b. Összefoglalva,

$\displaystyle FD\cdot FH={b(a-c)\over2(a+c)}\cdot{(a+c)(a-c)\over2b}=\Bigl({a-c\over2}\Bigr)^2=EF^2\ ,$

amint azt bizonyítanunk kellett. A megoldás során nem használtuk ki, hogy H az AC oldalra esik.

B.3538. Keressünk olyan pozitív valós számot, ami 2501-szeresére nő, ha a tizedestört alakjában fölcseréljük a tizedesvessző utáni első és ötödik számjegyet. (5 pont)

Megoldás. Jelölje a keresett számot X, a felcserélés után kapott számot pedig X'. Ha X$\displaystyle ge$0,1, akkor X'<10X. Ezért X<0,1, vagyis X=A+10^-5a és X'=A+10^-1a, ahol a 0-tól különböző számjegy, A pedig olyan 0,1-nél kisebb pozitív szám, melynek a tizedesvessző utáni ötödik számjegye 0. Az X'=2501X feltétel alapján

$\displaystyle A={7499a\over2500}\cdot{1\over10^5}\ .$

Ezért a-t úgy kell meghatároznunk, hogy a 7499a/2500 szám tizedesvesszőt megelőző számjegye 0 legyen. Mivel 7499/2500 3-nál éppen csak egy picivel kisebb, ez pontosan az a=7 esetben fog teljesülni, ahonnan A=0,000209972 és X=0,000279972 adódik. Ennek a számnak 2501-szerese, 0,700209972 valóban a kívánt módon állítható elő X-ből. A feladatnak tehát ez az egyetlen megoldása.

B.3539. Egy ládában 8 darab törékeny tárgy van. Közülük 1 db 50 000 Ft, 3 db 30 000 Ft és 4 db 20 000 Ft értékű. A ládát szállítás során leejtik, a tárgyak egymástól függetlenül 1/2 valószínűséggel törnek össze. Mennyi annak a valószínűsége, hogy a kár nem haladja meg a 100 000 Ft-ot? (4 pont)

Megoldás. Jelölje P(A_i) (0$\displaystyle le$i$\displaystyle le$1), P(B_i) (0$\displaystyle le$i$\displaystyle le$3) és P(C_i) (0$\displaystyle le$i$\displaystyle le$4) annak a valószínűségét, hogy az 50.000 Ft, a 30.000 Ft, illetve a 20.000 Ft értékű tárgyakból pontosan i darab törik össze, ekkor

$\displaystyle P(A_i)={1\over2}{1\choose i},P(B_i)={1\over2^3}{3\choose i};P(C_i)={1\over2^4}{4\choose i},$

hiszen a tárgyak egymástól függetlenül 1/2 valószínűséggel törnek össze. Annak valószínűsége, hogy az 50.000 Ft, a 30.000 Ft, illetve a 20.000 Ft értékű tárgyakból rendre i, j, k darab törik össze, éppen P(A_i)P(B_j)P(C_k), az események függetlensége miatt. A rövidebb számolás kedvéért vezessük be a

$\displaystyle P(B_{\le i})=\sum_{j=0}^iP(B_j);P(C_{\le i})=\sum_{j=0}^iP(C_j),$

mennyiségeket is. Ha nem törik össze az 50.000 Ft-os tárgy és a 30.000 Ft értékűek közül egyik sem, akkor a 20.000 Ft-osak közül akármennyi törik is össze, a kár értéke nem haladja meg a 100.000 Ft-ot. Ennek az eseménynek a valószínűsége P(A₀)P(B₀)=1/16. Hasonlóképpen szisztematikusan számba véve az összes lehetőséget kapjuk, hogy a keresett valószínűség

$\displaystyle P={1\over16}+P(A_0)\Bigl(P(B_1)P(C_{\le3})+P(B_2)P(C_{\le2})+P(B_3)P(C_0)\Bigr)+$

$\displaystyle +P(A_1)\Bigl(P(B_0)P(C_{\le2})+P(B_1)P(C_{\le1})\Bigr)=$

$\displaystyle ={1\over16}+{1\over2}\Bigl({3\over8}\cdot{15\over16}+{3\over8}\cdot{11\over16}+{1\over8}\cdot{1\over16}\Bigl)+{1\over2}\Bigl({1\over8}\cdot{11\over16}+{3\over8}\cdot{5\over16}\Bigr)={121\over256}\ .$

B.3540. Milyen határok között változik a háromszögekben a magasságok négyzetösszegének és az oldalak négyzetösszegének az aránya? (5 pont)

Balogh János (Kaposvár) javaslata nyomán

Megoldás. A szokásos jelölésekkel, a $\displaystyle T=\sqrt{s(s-a)(s-b)(s-c)}$ Héron-képletet és a 2T=am_a=bm_b=cm_c összefüggéseket felhasználva a keresett arány

$\displaystyle x={1\over4}\Bigl({1\over a^2}+{1\over b^2}+{1\over c^2}\Bigr){(a+b+c)(a+b-c)(b+c-a)(c+a-b)\over a^2+b^2+c^2}\ .$

Ha a=b=c=1, akkor x=3/4, az elfajuló a=b=1, c=2 esetben pedig x=0. Rögzített a=b=1 mellett minden 1$\displaystyle le$c<2 esetben létezik a,b,c oldalú háromszög. Továbbá 1$\displaystyle le$c$\displaystyle le$2 esetén az x=x(c) c-nek folytonos függvénye. Innen látszik, hogy a szóban forgó arány a (0,3/4] intervallumban tetszőleges értéket felvehet. A továbbiakban megmutatjuk, hogy az arány a 3/4 értéket nem haladhatja meg.

Ehhez az

$\displaystyle {(a^2b^2+b^2c^2+c^2a^2)(2a^2b^2+2b^2c^2+2c^2a^2-a^4-b^4-c^4)\over a^2b^2c^2(a^2+b^2+c^2)}\le3$

egyenlőtlenséget kell igazolni, valahányszor a,b,c egy háromszög oldalai. Az a²=x>0, b²=y>0, c²=z>0 jelöléseket alkalmazva látszik, hogy ez következik a

$\displaystyle \Bigl(2(xy+yz+zx)-x^2-y^2-z^2)\Bigr)(xy+yz+zx)\le3(x+y+z)xyz$

egyenlőtlenségből, ami viszont tetszőleges x,y,z nem negatív számokra teljesül.

Valóban, a beszorzást elvégezve, rendezés után látható, hogy ez az egyenlőtlenség ekvivalens az

x³y+xy³+y³z+yz³+z³x+zx³-2(x²y²+y²z²+z²x²)$\displaystyle ge$0

egyenlőtlenséggel, ami továbbá ekvivalens az

xy(x-y)²+yz(y-z)²+zx(z-x)²$\displaystyle ge$0

egyenlőtlenséggel. Ez utóbbi pedig nyilván teljesül tetszőleges x,y,z nem negatív számokra. Az is látszik, hogy x,y,z>0 esetén egyenlőség csak az x=y=z esetben állhat fenn. Ezért a feladatban szereplő arány pontosan akkor veszi fel a maximális 3/4 értéket, ha a háromszög szabályos.

B.3541. Legyen $\displaystyle f(x)={ax+b\over cx+d}$. Bizonyítsuk be, hogy ha f(f(f(1)))=1, és f(f(f(2)))=3, akkor f(1)=1. (5 pont)

Megoldás. Megengedett függvény alatt értsünk tetszőleges, a valós számok egy véges részhalmazától eltekintve minden valós számon értelmezett, $\displaystyle {ax+b\over cx+d}$ alakú függvényt, mely az értelmezési tartományán nem konstans. A függvény együtthatóira nézve ez azt jelenti, hogy ad-bc$\displaystyle ne$0. Egyszerű számolással ellenőrizhetjük, hogy egy ilyen függvény tetszőleges értéket legfeljebb egyszer vehet fel. Az $\displaystyle f(x)={ax+b\over cx+d}$ és $\displaystyle g(x)={a'x+b'\over c'x+d'}$ megengedett függvények kompozíciója a szintén megengedett

$\displaystyle (f\circ g)(x)={(aa'+bc')x+(ab'+bd')\over(ca'+dc')x+(cb'+dd')}$

függvény. Valóban, az (aa'+bc')(cb'+dd')-(ab'+bd')(ca'+dc')= egyenlőségből (a'd'-b'c')(bc-ad)=0 következne, ami lehetetlen. Végül, az fog függvény pontosan azokon az x helyeken nincs értelmezve, ahol vagy g(x) nincs értelmezve (ebből véges sok van), vagy f(g(x)) nincs értelmezve (ebből is véges sok van), vagy pedig x=-(cb'+dd')/(ca'+dc') (ilyenből legfeljebb egy van).

Mivel a F=fofof függvény az értelmezési tartományán nem konstans, az f függvény sem lehet az, ezért az előbbiek alapján F megengedett függvény, melynek az 1 szám fixpontja: F(1)=1. Hány fixpontja lehet egy megengedett függvénynek? A $\displaystyle h(x)={Ax+B\over Cx+D}=x$ feltétel (a h értelmezési tartományán) ekvivalens a Cx²+(D-A)x-B=0 feltétellel. Ezért h-nak legfeljebb 2 fixpontja lehet, kivéve ha C=D-A=-B=0, amikor is h(x)=x a h függvény értelmezési tartományán, melynek minden eleme egyben h-nak fixpontja lesz.

Mivel F(2)$\displaystyle ne$2, az F függvénynek legfeljebb 2 fixpontja van, ebből az egyik az 1. Ha f(1)$\displaystyle ne$1, akkor tekintsük az u=f(1) és v=f(u) számokat, ezeken f értelmezve van és f(v)=1. Ha u=v, akkor 1=f(f(u))=f(f(v))=f(1), ha pedig v=1, akkor szintén 1=f(v)=f(1), ami ellentmondás. Továbbá

F(u)=(Fof)(1)=(fofofof)(1)=(foF)(1)=f(1)=u

és hasonlóképpen

F(v)=(Fof)(u)=(fofofof)(u)=(foF)(u)=f(u)=u ,

vagyis 1,u,v az F függvénynek 3 különböző fixpontja. Ez az ellentmondás igazolja, hogy f(1)=1.