A 2002. májusi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3531. Néhány kiránduló a Tiszán csónakot bérelt 3 órára. A folyó sebessége 2,5 km/h, a csónaké a vízhez képest 7,5 km/h. Mennyire távolodhatnak el a kikötőtől, ha 3 óra alatt vissza akarnak érni? (3 pont)

Szolnok megyei általános iskolai verseny

Megoldás. Ha a folyó sebessége u, ehhez képest pedig a csónak v-vel képes haladni, a legnagyobb távolság, amire eltávolodhat, hogy még t időn belül visszaérjen

$\displaystyle s=t{v^2-u^2\over2v}=10~\rm km.$

P. 3532. Az ábrán látható nyújthatatlan fonál felső végét a mennyezethez rögzítjük, az alsó végére pedig egy m tömegű testet kötünk. A test alsó részéhez egy rugót erősítünk, amelyen 2m tömegű test lóg. A rendszer egyensúlyban van. A rugó megnyúlása 30 cm. Égessük el a fonalat!

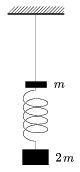
a) Mekkora az egyes testek gyorsulása közvetlenül a fonál elégetése után?

b) Mennyi idő múlva lesz a rugó először nyújtatlan állapotban, és mekkora a testek sebessége ebben a pillanatban? (5 pont)

Közli: Szűcs József, Pécs

(Párkányi László fizikaverseny)

Megoldás. a) Kezdetben a rugót F=2mg erő feszíti, ezért a fonal elégetésének pillanatában a felső testre 3mg erő hat, az alsó testre ható erők eredője pedig 0. Ennek megfelelően a₁(0)=3g, a₂(0)=0.

b) Az egyes testek mozgásegyenletei

ma₁=mg+kx, 2ma₂=2mg-kx ,

ahol x a rugó megnyúlása. Ezekből az x mennyiség a=a₂-a₁ gyorsulására a következőt kapjuk:

$\displaystyle a=-{3k\over2m}x.$

Ez a rezgőmozgás ismert egyenlete, melynek megoldása

x(t)=Acos $\displaystyle \omega$t $\displaystyle \left(\omega=\sqrt{{3k\over2m}}\right)$.

Mivel az A amplitúdó azonos a 30 cm-es kezdeti megnyúlással, k=2mg/A, így $\displaystyle \omega=\sqrt{3g/A}=10~{\rm s}^{-1}$. A rugó az indítás után először T/4=$\displaystyle \pi$/(2$\displaystyle \omega$)=0,16 s idő múlva lesz nyújtatlan állapotban.

P. 3533. Egy 10 000 m²-es sík területre időben egyenletesen, a hely szempontjából pedig egyenletes rendezetlenségben 41 másodpercig esik a jég. Az egyforma, gömböknek tekinthető jégdarabok olyan talajra hullanak, amelybe csupán kissé nyomódnak bele, ugyanakkor csak azok mozdulnak tovább beérkezési helyükről, amelyek a társaikra estek. Az utolsó másodpercben lehullott 20 000 jégdarab közül 200 esett az első 40 másodpercben lehullott valamelyik társára. a) A terület hány százalékát borítja jég? b) Mekkora egy jéggömb főkörének területe? (5 pont)

Közli: Édes Zoltán, Tata

Megoldás. Legyen a teljes terület A (A=10 000 m²), egy jégdarab főkörének a területe pedig a. Az első 40 s alatt 40-szer annyi jég esik, mint az utolsóban, azaz a 40. másodperc végén a lefedett terület 800 000 a. Ez úgy aránylik a teljes területhez, mint a 200 a 20 000-hez (elhanyagoljuk annak a leletőségét, hogy az utolsó másodperc alatt leesett jég eshet ugyancsak az utolsó másodperc alatt leesett jégre, ez kisebb mint 1/40-ed relatív hibát okozhat). Eszerint A=8^.10⁷a, azaz a=1,25 cm². A teljes lefedett terület a jégeső után 820 000 a, ez az A-nak 1,025%-a.

P. 3534. 20 cm vastag, 0 ^oC hőmérsékletű, 0,25 kg/dm³ sűrűségű hótakaróból milyen vastag réteg olvad meg a napsugárzás hatására 5 órányi, a hóréteggel átlagosan 25^o-os szöget bezáró napsütés esetén? A Napból a légkör felső határán minden 1 m² nagyságú, a sugárzásra merőleges felületre érkező sugárzási teljesítmény átlagosan 1350 W. Ennek 50%-a elnyelődik a légkörben, és a hó a leérkező energia 90%-át visszaveri. (4 pont)

Közli: Holics László, Budapest

Megoldás. A hóréteg egy négyzetmétere 513,4 kJ energiát nyel el öt óra alatt, ez 1,54 kg jég felolvasztására elég, ennyi jég pedig egy négyzetméteren 6,2 mm-es réteg hóban van.

P. 3535. Az ábrán látható, egyik végén beforrasztott, A keresztmetszetű, derékszögben kétszer meghajlított cső függőleges síkban helyezkedik el. A cső függőleges részében lévő, kezdetben L=38 cm hosszúságú és T₀ hőmérsékletű levegőoszlopot 2L hosszúságú higanyoszlop zárja el. A cső vízszintes részének hosszúsága L. A külső p₀ légnyomás 2L magasságú higanyoszlop hidrosztatikai nyomásával egyenlő. Jelöljük L^.A-t V₀-lal!

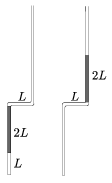
a) Adjuk meg p₀V₀ egységekben, hogy mekkora munkát végez a táguló levegő azon folyamat során, mialatt a higany éppen átfolyik a felső függőleges csőbe.

b) A levegővel közölt hő hány százaléka növelte a belső energiát?

c) Ábrázoljuk a levegő hőmérsékletét a térfogat függvényében! (5 pont)

Közli: Kotek László, Pécs

(Mikola-verseny, Sopron)

Megoldás. a) Kezdetben a bezárt levegő nyomása 2p₀. Ez, miközben a levegő V₀-ról 2V₀-ra tágul, a térfogattal lineárisan változva 3p₀/2-re csökken. A $\displaystyle 2V_0\to3V_0$ tágulás során a nyomás nem változik, majd az utolsó $\displaystyle 3V_0\to4V_0$ szakaszon a térfogattal lineárisan változva visszanő az eredeti 2p₀ értékre. A táguló levegő munkáját a p(V) görbe alatti terület adja, ez 5p₀V₀.

b) A folyamat során a levegő hőmérséklete a gáztörvény szerint T₀-ról 4T₀-ra nő, tehát a belső energiája (5/2)nR3T₀ értékkel nő. Kihasználva, hogy nRT₀=2p₀V₀, ez 15p₀V₀, ami a teljes 20p₀V₀ hőfelvétel 75%-a.

c) Mérjük a térfogatot V₀, a nyomást 2p₀ és a hőmérsékletet T₀ egységekben, és legyenek rendre v=V/V₀, x=p/(2p₀) és $\displaystyle \tau$=T/T₀! Ekkor

$\displaystyle \tau$=xv, ahol $\displaystyle x=\cases{ 1-(v-1)/4=(5-v)/4,{\rm\ ha\ }1\leq v\leq2;\cr3/4,{\rm\ ha\ }2\leq v\leq3;\cr3/4+(v-3)/4=v/4,{\rm\ ha\ }3\leq v\leq4.\cr}$

Ennek megfelelően a hőmérséklet a térfogat függvényében egy olyan görbe, amely egy lefelé nyitott parabolából, egy egyenes szakaszból és egy felfelé nyitott parabolából rakható össze.

P. 3536. 5 keV energiájú, kicsit széttartó elektronnyaláb érkezik homogén mágneses mezőbe. A részecskék sebessége B irányával kicsiny szöget zár be. Mekkora legyen a mágneses indukció értéke, hogy az elektronok 10 cm távolságonként újra és újra egy pontban találkozzanak? (5 pont)

Tornyai Sándor verseny, Hódmezővásárhely

Megoldás.

$\displaystyle B={2\pi\over d}\sqrt{{2mU\over e}}=15~{\rm mT}.$

P. 3537. A Compton-szórás (rugalmas foton-elektron ütközés) során a meglökött - kezdetben nyugvónak tekintett - elektron lendülete nagyobb lett, mint a beeső f frekvenciájú fotoné volt. Legalább mekkora szögben szóródott a foton? (5 pont)

Közli: Varga István, Békéscsaba

Megoldás. Vizsgáljuk a határesetet, amikor a meglökött elektron impulzusa éppen akkora, mint a bejövő fotoné volt, azaz

mv=hf/c,

és engedjük meg, hogy v akár relativisztikus sebesség is lehessen, azaz számoljunk az

$\displaystyle m={m_0\over\sqrt{1-{v^2/c^2}}}$

relativisztikus tömegképlettel! Ha a szóródó foton frekvenciája $\displaystyle f^{\prime}$, az energiamegmaradás miatt

$\displaystyle hf^{\prime}=hf-(mc^2-m_0c^2).$

A relativisztikus tömegre igaz, hogy

(mc²)²-(mv)²c²=(m₀c²)².

Ez a fenti összefüggéssel együtt

$\displaystyle mc^2=\sqrt{m_0^2c^4+h^2f^2},$

azaz

$\displaystyle hf^{\prime}=hf-\left(\sqrt{m_0^2c^4+h^2f^2}-m_0c^2\right).$

Jelölje $\displaystyle \vartheta$ a foton impulzus eredeti és szórás utáni irányának a szögét! Az impulzusmegmaradás miatt a bejövő foton lendülete, a szóródó foton lendülete, valamint a meglökött elektron lendülete háromszöget alkot. Ez a háromszög a vizsgált határesetben éppen egyenlő szárú, és a keresett $\displaystyle \vartheta$ szög az alapon fekvő egyik szög. Ebből

$\displaystyle \cos\vartheta={f^{\prime}\over2f}= {1\over2}\left(1+K-\sqrt{K^2+1}\right),$

ahol K=m₀c²/(hf). Mivel az

$\displaystyle f(x)=1+x-\sqrt{x^2+1}$

függvény minden minden x-re 1-nél kisebb, cos $\displaystyle \vartheta$<1/2, azaz $\displaystyle \vartheta$>60^o.

A $\displaystyle \vartheta$=60^o-os határt K$\displaystyle \gg$1, vagyis hf$\displaystyle \ll$m₀c² határesetben közelíthetjük meg, vagyis akkor, amikor a bejövő foton energiája lényegesen kisebb, mint az elektron nyugalmi energiája. Mivel ez a nemrelativisztikus tartomány, a foton szórási szögének legkisebb értékére akkor is megkaptuk volna a helyes 60^o-os határt, ha mindvégig a klasszikus (newtoni) fizika képleteivel számolunk.

P. 3538. Egy elektron mozgási energiája n-ed része, lendülete n-szerese valamely foton energiájának, illetve lendületének. Mekkora n értékek esetén láthatók az ilyen fotonok? (4 pont)

A Budó-verseny egyik feladata nyomán

Megoldás. Tételezzük fel, hogy az elektron sebessége sokkal kisebb, mint a fénysebesség. Az mv²/2=hf/n, mv=nh$\displaystyle \lambda$ valamint a $\displaystyle \lambda$=c/f összefüggésekből

$\displaystyle n^3={2mc\lambda\over h}.$

Ha a fény látható, akkor 380 nm<$\displaystyle \lambda$<760 nm, ebből 68$\displaystyle \le$n$\displaystyle \le$86.

Az elektron sebességének és a fénysebességnek az aránya

$\displaystyle {v\over c}={2\over n^2}\ll1,$

tehát valóban jogos volt a nemrelativisztikus energiaképlet használata.

P. 3539. Kinyújtott kezünkben tartunk egy f=12 cm fókusztávolságú gyűjtőlencsét, melyen át egy 60 méterre lévő, 24 méter magas tornyot figyelünk. Becsült adatok felhasználásával határozzuk meg a szemünk retináján létrejövő kép nagyságát! Hányszor nagyobbnak vagy kisebbnek látjuk a tornyot a lencsén keresztül, mint szabad szemmel? Hány dioptriás a szemünk az egyik, illetve a másik esetben? (5 pont)

Közli: Honyek Gyula, Budapest

Megoldás. Karunk hossza kb. 60 cm, szemünk átmérője kb. 2,4 cm. Ha a lencsén keresztül nézzük a tornyot, valójában a szemünktől 60 cm-12 cm=48 cm-re keletkezett 4,8 cm-es (fordított állású) képet nézzük, tehát a tárgytávolság 48 cm, a tárgy nagysága 4,8 cm, a képtávolság pedig a szemünk mérete, azaz 2,4 cm. Ezekből a retinán létrejövő kép nagysága 0,24 cm, szemünk fókusztávolságának a reciproka pedig 43,7 m^-1.

A tornyot szabad szemmel nézve a tárgytávolság 60 m, a tárgy nagysága 24 m, a képtávolság pedig ugyanannyi, mint az előző esetben. Ekkor a torony képe a retinán 9,6 mm, és ilyenkor a szemünk dioptriája 41,7 m^-1.

P. 3540. A napkitöréseket figyelő SOHO műhold mindig a Napot és a Földet összekötő egyenesen helyezkedik el. Milyen messze van a SOHO a Földtől? (A Föld pályáját tekintsük körnek!) (6 pont)

Közli: Korpássy Péter, Budapest

Megoldás. A SOHO távolsága a Föld középpontjától kb. 1,5^.10⁶ km.