A számítástechnika-versenyben kitűzött feladatok 2002. szeptember

Kérjük, olvassa el a versenykiírást.

I. 31. Az ókori Egyiptomban a 0 és 1 közötti racionális számokat egységtörtek összegeként \(\displaystyle \frac{1}{x_1}+\frac{1}{x_2}+\ldots+\frac{1}{x_k}\)alakban adták meg, ahol az x_i-k különböző pozitív egész számok.

Például

\(\displaystyle \frac{2}{5}=\frac{1}{3}+\frac{1}{15},\quad\frac{9}{11}=\frac{1}{2}+\frac{1}{4}+\frac{1}{15}+\frac{1}{660},\quad\frac{19}{30}=\frac{1}{2}+\frac{1}{8}+\frac{1}{120}. \)

Készítsünk programot (I31.pas, ...), amely adott M (1 \(\displaystyle \le\)M<N) és N (2 \(\displaystyle \le\)N \(\displaystyle \le\)30) természetes számokra megadja M/N egységtörtekre bontását!

(10 pont)

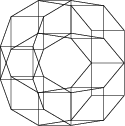
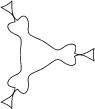
I. 32. Kettőspoligont úgy kapunk, hogy két szabályos sokszöget ,,összefésülünk'', azaz az oldalaikat felváltva rajzoljuk le. (Az alábbi ábrán egy négyzetet és egy háromszöget fésültünk össze úgy, hogy mindkettőből 3 oldalt rajzoltunk meg. Ha 4 oldalt rajzolnánk, akkor a V₂ vektorhoz az U₃ vektort kellene illesztenünk, ahhoz pedig ismét a V₀ vektort.)

A multipoligon ugyanígy készül, csak nem kettő, hanem több szabályos sokszögből.

Készítsünk programot (I32.pas, ...), amely beolvassa az összefésülendő sokszögek számát (1 \(\displaystyle \le\)DB \(\displaystyle \le\)100) és a mindegyikükből rajzolandó oldalak számát (1 \(\displaystyle \le\)N \(\displaystyle \le\)360), az egyes sokszögek oldalhosszát (1 \(\displaystyle \le\)H(i) \(\displaystyle \le\)100) és külső szögét (-120 \(\displaystyle \le\)S(i) \(\displaystyle \le\)120), majd kirajzolja a belőlük összeállított multipoligont!

Példa:

DB=2, N=3 H=50, SZ=90 H=50, SZ=120	DB=2, N=40 H=50, SZ=90 H=50, SZ=-40	DB=2, N=360 H=0.5, SZ=1 H=1, SZ=-1	DB=4, N=360 H=1, SZ=1 H=1, SZ=-8 H=1, SZ=16 H=1, SZ=-2

(10 pont)

I. 33. Jóska és Pista számjátékot játszanak. Első lépésként felsorolnak N (1 \(\displaystyle \le\)N \(\displaystyle \le\)100) természetes számot, majd eldöntik, hogy mindegyikük M (1 \(\displaystyle \le\)M \(\displaystyle \le\)N) számot fog választani közülük. Szabályosan választanak, Jóska minden A-adik számot (1 A N), Pista pedig minden B-ediket (1 B N). Ha a sorozat végére érnek, elölről folytatják, azaz pl. az N+1. szám a felsorolás első tagja lesz, az N+2. a második és így tovább. Az győz, aki a kiválasztott számait összeadva nagyobb számot kap.

Készítsünk táblázatot (I33.xls), amelyben N, M, A, B megadása esetén megtudjuk, hogy ki győzött. A győztes betűjele (A vagy B) a táblázatban piros, a vesztesé pedig kék színű legyen! Döntetlen játék esetén mindkettőt feketével kell írni.

Példa:

(10 pont)

A számítástechnike feladatok megoldásai a következő címre küldendők:

A beküldési határidő: 2002. október 13.