 |
A 2003. januári informatika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
I. 40. Az ábrán egy 5x5-ös táblázat minden sora, minden oszlopa és a két főátlója egy-egy ötjegyű prímszámnak olvasható. A sorokat balról jobbra, az oszlopokat fölülről lefelé, a két főátlót pedig balról jobbra kell kiolvasni.
|
Írjunk programot (I40.pas, ...), amely beolvassa a prímszámok számjegyeinek összegét, valamint a bal felső sarokba írandó számjegyet, s ezek alapján egy ilyen táblázatot készít.
Példa: Számjegyek összege=11, bal felső sarok számjegye=1.
(10 pont)
Megoldás:
Típus PrímTömb = Tömb(0..49999:Egész); Konstans Divisor : Tömb(0..4:Egész)=(10000,1000,100,10,1); Bits : Tömb(0..9:Egész)=(1,2,4,8,16,32,64,128,256,512); Változó Prime : PrímTömb; NextNumber : Tömb(0..9999:Egész); Sum,nPrimes : Egész; FirstNumber,i,j,k : Egész; VerticalPrimeStart : Tömb(0..5,0..5:Egész); Kvadrat : Tömb(0..4:Egész); w : Egész;Az adatok beolvasása, majd a páratlan prímek kiszámítása.
Be: Sum;
Be: FirstNumber;
i:=3;
ciklus
Ha Prime^[i SHR 1]
akkor
j:=i*i;
ciklus amíg j<100000
Prime^[j SHR 1]:=False;
Inc(j,i+i);
ciklus vége;
Elágazás vége;
i:=i+2;
amíg i<=320
ciklus vége;
A jegyek összegének ellenőrzése.
ciklus i:=0-től 49999-ig
Ha Prime^[i]
akkor
Ha DigitSum(i+i+1)<>Sum
akkor
Prime^[i]:=HAMIS
különben
nPrimes:=nPrimes+1;
elágazás vége;
elágazás vége;
ciklus vége;
Megkeressük az összes lehetséges jegyet, amivel a prímszám kezdődhet.
ciklus i:=1-től 4-ig
ciklus j:=5000-től 49999-ig
Ha Prime^[j]
akkor
k:=(j+j+1) DIV Divisor[i-1];
w:=Bits[((j+j+1) DIV Divisor[i]) MOD 10];
NextNumber[k]:=NextNumber[k] vagy w;
elágazás vége;
ciklus vége;
ciklus vége;
NextNumber[0]:=1023-1;
VerticalPrimeStart[1,0]:=FirstNumber;
Végül legeneráljuk a prímeket.
GenPrime(FirstNumber,1,0); algortimus vége.A szám számjegyeinek összegét adja vissza.
Függvény DigitSum(i : Egész) : Egész;A GenPrime eljárás generálja a prímeket. Paraméterkent átadjuk a p prím első részét, az n hosszát illetve az aktuális sor számát (-1).
Eljárás GenPrime(p,n,nn : Egész);
Változók
a,i,vp : Egész;
vp:=VerticalPrimeStart[nn,n];
Kiszámítjuk az összes lehetséges számot a következő számjegyhez.
a:=NextNumber[vp] and NextNumber[p];
vp:=vp*10;
Ha n<4
akkor
Legeneráljuk a következő számot.
p:=p*10;
Ciklus i:=0-től 9-ig
Ha (a és Bits[i])>0
akkor
VerticalPrimeStart[nn+1,n]:=vp+i;
GenPrime(p+i,n+1,nn);
elágazás vége;
ciklus vége;
különben
Vagy rekurzívan kitöltjük a következő sort.
ciklus i:=0-től 9-ig
Ha (a és Bits[i])>0
akkor
VerticalPrimeStart[nn+1,n]:=vp+i;
Kvadrat[nn]:=p*10+i;
TryLine(nn+1);
elágazás vége;
ciklus vége;
elágazás vége;
eljárás vége;
Eljárás TryLine(n : Egész);
Változók
i,j,k : Egész;
s : Szöveg;
Ha n<5
akkor
Legeneráljuk a következő sort.
GenPrime(0,0,n)
különben
Készen vagyunk a generálással, ezért leellenőrizzük a négyzetet. Ha jó, akkor megvan az eredmény.
j:=0; k:=0;
Ciklus i:=0-től 4-ig
j:=j*10+(Kvadrat[i] DIV Divisor[i]) MOD 10;
k:=k*10+(Kvadrat[4-i] DIV Divisor[i]) MOD 10;
ciklus vége;
Ha Prime^[j SHR 1] és Prime^[k SHR 1]
akkor
Ciklus i:=0-tól 4-ig
Ki: Kvadrat[i];
ciklus vége;
Eláagzás vége;
elágazás vége;
eljárás vége;
I. 41. Egy négyzetet sötét és világos mezőkre osztunk. A négyzet tükörtengelyeire tükrözésével, valamint a négyzet forgatásával újabb ábrákat kaphatunk (nem biztos, hogy nem egyezik meg a kiinduló ábrával, vagy valamelyik másik transzformáció, transzformációk eredményével).
Készítsünk programot (I41.pas, ...), amely beolvassa egy NxN-es négyzet kitöltését (sorfolytonosan S vagy V betűket írhatunk be), majd kirajzolja a négyzetet és az összes különböző képet.
Példa: N=3, négyzet=((S,S,V),(V,V,V),(V,S,S)) esetén a kezdőkép és a transzformáltak:
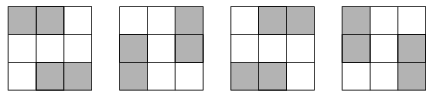
(10 pont)
Megoldás:
Maximum 50x50-es lehet a négyzet. Egy három dimenziós tömbben tároljuk az állapotokat, ahol az első index mutatja meg, hogy melyik transzformált állapotról van szó.
Algoritmus Jan2;
Típus
Tnegyzet=Tömb(1..8,1..50,1..50:Karakter);
Változó
n,i,j,t,t2:Egész;
negyzet:Tnegyzet;
Beolvassuk a négyzet méretét illetve a mezők színeit.
Be: A négyzet mérete (0<N<51): N;;
t:=1;
Ciklus i:=1-től N-ig
ciklus j:=1-től N-ig
Be: A mező színe (S,V): negyzet[t,i,j];
ciklus vége;
ciklus vége;
Transzformálunk majd kirajzoltatjuk a négyzeteket.
Transzformal; Kirajzol; algoritmus vége.Egy négyzetet 8 féle képpen lehet transzformálni. Tükrözni illetve 90°-kal elforgatni. Ebben az eljárásban az összes lehetséges állapotot előállítjuk.
Eljárás Transzformal;
Változók
i,j:Egész;
t2:=t;
ciklus amíg t<8
t:=t+1;
t2:=t2+1;
Egyszer tükrözünk. Az első állapotot.
Ha t=5
akkor
{tukrozes - elsoe}
ciklus i:=1-től n-ig
ciklus j:=1-től n-ig
negyzet[t2,i,j]:=negyzet[1,i,N+1-j];
ciklus vége;
ciklus vége;
Máskor forgatjuk az előzőt.
különben
{forgatas - elozoe}
ciklus i:=1-től n-ig
ciklus j:=1-től n-ig
negyzet[t2,i,j]:=negyzet[t2-1,j,N+1-i];
ciklus vége;
ciklus vége;
elágazás vége;
ciklus vége;
eljárás vége
A következő eljárásban ellenőrizzük, hogy az aktuális állapotot már kirajzoltuk-e vagy sem, és ha nem akkor most megtesszük.
Eljárás Kirajzol;
ciklus t:=1-től t2-ig
Ha kulonbozik(t)
akkor
ciklus i:=1-től n-ig
ciklus j:=1-től n-ig
Ki: negyzet[t,i,j];
ciklus vége;
ciklus vége;
elágazás vége;
ciklus vége;
Eljárás vége;
A kulonbozik nevű függvény ellenőrzi le, hogy a t2-edik négyzetet rajzoltuk-e már, vagyis szerepelt-e már ez a festés az előtte levő állapotok között (más-e, mint a többi).
Függvény kulonbozik(t2:Egész):Logikai;
Változók
t3:Egész;
k:Logikai;
k:=TRUE;
t3:=1;
ciklus amíg (t3<t2) és mas(t3,t2)
t3:=t3+1;
ciklus vége;
Ha (t3<t2)
akkor k:=HAMIS;
elágazás vége;
kulonbozik:=k;
függvény vége;
Akkor más a t3 indexű négyzet, mint a t2, ha az összes, mind az n-négyzet helyen különbözik tőle.
Függvény mas(t3,t2:Egész):Logikai;
Változók
m:Logikai;
k:Egész;
m:=HAMIS;
k:=0;
ciklus amíg (k<n*n) és (negyzet[t3,(k div n)+1,k mod n+1]=
negyzet[t2,(k div n)+1,k mod n+1])
k:=k+1;
ciklus vége;
Ha k<n*n
akkor m:=TRUE;
elágazás vége;
mas:=m;
függvény vége;
I. 42. Egy táblázatban tároljuk néhány valutáról, hogy 100 egység belőle hány forintot ér. Például 100 ausztrál dollár (AUD) 13 279 forint.
Készítsünk táblázatot (I42.xls), amelyben konstans valutatáblázatot használva a harmadik oszlopba bármelyik (de csak egy) valuta mellé beírva tetszőleges összeget, a táblázatkezelő kiszámolja, hogy ennyiért melyik valutából mennyit lehet kapni.
Példa:
|
|
(10 pont)
Megoldás:
Az első oszlopban tároljuk a valutákat, a másodikban azt, hogy ezek 100 egysége mennyi forintot ér. A harmadik oszlopba kell írni, hogy valamelyik valutából mennyit váltunk. A negyedikben oszlopban jelenik meg az eredmény. Míg a "G" és "H" jelű oszlopokat segítségül hívjuk.A "G"-be 0-t vagy 1-t írunk a szerint, hogy a harmadik oszlopba írtunk-e valamit, vagyis abban a sorban szereplő valutát akarjuk-e váltani. A "H"-ba pedig átmásoljuk a harmadik oszlopbeli értékeket. Így:
G8:=HA(C8="";0;1) H8:=C8A "D" jelű oszlopba pedig kiszámoljuk az eredményt. Először az átváltandó valuta értéke kell. Ezt átmásoltuk a H oszlopba, és azzal kell számolni, ahol a G oszlopban egyes (1) szerepel (FKERES). Megkeressük választott valuta forintbeli értékét és összeszorozzuk a valuta mennyiségével, így mostantól forintban számolunk (INDEX). Ezt a szorzatot el kell osztanunk a megfelelő sorban szereplő valuta forintbeli értékével vagyis a második sozlopbeli értékkel.
D8:=FKERES(1;
$G$5:$H$14;
2;
HAMIS
) *
INDEX($B$5:$B$14;
HOL.VAN(1;
$G$5:$G$14;
0);
1
)/
B8

