A 2003. januári számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3581. A világ egyik legnagyobb gyémántja 44,5 karátos, csaknem tiszta szén. Hány szénatom van ebben az óriás kristályban?

(3 pont)

Közli: Radnóti Katalin, Budapest

Megoldás. 4,5^.10²³ db.

P. 3582. Légpárnás asztalon három egyforma korong van, tömegeloszlásuk egyenletes. Két korong érintkezik egymással, ezek nem mozognak. A harmadik korong feléjük tart, sebessége merőleges a két álló korong középpontját összekötő egyenesre. Adjuk meg a tökéletesen rugalmas és súrlódásmentes ütközések utáni sebességek arányát az ábrán látható szög függvényében!

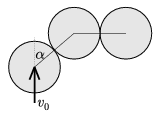
(5 pont)

Közli: Simon Péter, Pécs

Megoldás. Úgy tekinthetjük, hogy először a bejövő golyó ütközik a bal oldali állóval, majd az meglöki a jobb oldalit. (Nagyon szorosan illeszkedő korongok ütközés elvben lejátszódhat másképp is: a második ütközés már azalatt ,,megkezdődhet'', amikor az első ütközés még be sem fejeződött. A gyakorlatban azonban ez nem valósul meg; gondoljunk az ingasorban felfüggesztett golyók ütközésére!)

Azonos tömegű testek teljesen rugalmas ütközésekor az érintkezési felületre merőleges (normális) irányú sebességkomponensek kicserélődnek, az érintősíkban felvő komponensek pedig változatlanok maradnak. Ennek alapján a kimenő sebeségek nagyságainak aránya

sin $\displaystyle \alpha$ : cos²$\displaystyle \alpha$ : cos $\displaystyle \alpha$sin $\displaystyle \alpha$.

P. 3583. Egy R=20 cm sugarú, vízszintes tengelyű, rögzített csőben egy r=6 cm sugarú tömör gömböt kissé kimozdítunk egyensúlyi helyzetéből, majd elengedünk. Mekkora periódusidejű mozgás jön létre, ha a gömb csúszás nélkül gördül a csőben? Legfeljebb mekkora lehet a mozgás amplitúdója, ha a tapadó súrlódás együtthatója $\displaystyle \mu$=0,05?

(5 pont)

Közli: Piacsek István, Sopron

Megoldás. A mozgásegyenletek:

$\displaystyle m(R-r)\beta=-mg\sin\varphi+S\,,\quad\quad\Theta\left(1-{R\over r}\right)\beta=rS\,,$

ahol $\displaystyle \varphi$ a gömb tömegközéppontjának szögkitérése, S a súrlódási erő, és $\displaystyle \Theta=(2/5)mr^2$. Kis kitérések esetén ezek az egyenletek egy

$\displaystyle T=2\pi\sqrt{7(R-r)\over5g}\approx0{,}9~\rm s$

rezgésidejű harmonikus rezgőmozgást írnak le.

Nincs megcsúszás még a szélső helyzetben sem, ha a legnagyobb szögkitérés

$\displaystyle \varphi_{\rm max}={\rm arc\,tg\,}{7\mu\over2}\approx0{,}175~{\rm rad} \approx10^\circ.$

Ekkora szögkitérésnél a mozgás már észrevehetően eltér a harmonikus rezgéstől.

P. 3584. Bizonyos mennyiségű héliumgáz állapotváltozását a pV³=állandó formula írja le. A folyamat végére a gáz abszolút hőmérséklete negyedére csökken, belső energiája 1800 J-lal változik. A folyamat során a gáz legkisebb nyomása 10⁵ Pa.

Ábrázoljuk a folyamatot a p-V diagramon a végpontok adatainak feltüntetésével!

(4 pont)

Közli: Kotek László, Pécs

Megoldás. A kezdővégállapotban

p₁=8^.10⁵ Pa,   V₁=2^.10^-3 m³,

a végállapotban pedig

p₂=10⁵ Pa,   V₂=4^.10^-3 m³.

P. 3585. Derékszögben meghajlított, igen nagy kiterjedésű, vékony fémlap mindkét lapjától egyaránt d távolságra elhelyezünk egy m tömegű, Q töltésű kicsiny testet, majd elengedjük.

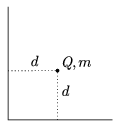
a) Mekkora gyorsulással indul el a test?

b) Mekkora lesz a sebessége, amikor már 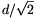utat megtett?

(A gravitáció hatását elhanyagolhatjuk.)

(5 pont)

Közli: Pálfalvi László, Pécs

Megoldás. A tükörtöltések módszerét lehet alkalmazni.

a)

$\displaystyle a={2\sqrt{2}-1\over8}\,{kQ^2\over md^2}$

b)

$\displaystyle v=\sqrt{{4-\sqrt{2}\over4}\,{kQ^2\over md}}.$

P. 3586. Egy űrhajóban V térfogatú, T hőmérsékletű, p₀ nyomású levegő van. Az űrhajó falán keletkezik egy A keresztmetszetű piciny lyuk, amelyen keresztül a benti levegő lassan szivárog kifelé.

Mennyi idő alatt csökken a benti levegő nyomása a felére? (Tegyük fel, hogy a benti levegő hőmérséklete nem változik!)

(5 pont)

Közli: Szilva Attila, Miskolc

Megoldás.

$\displaystyle T_{1/2}={V\ln2\over A}\sqrt{\rho_0\over2p_0}.$

P. 3587. Függőleges vezető tengelyhez elforgathatóan csatlakozik egy vízszintes fémrúd, amelynek másik vége egy l sugarú vezető körgyűrűre támaszkodik. A gyűrűt az ábra szerint egy R ellenálláson keresztül vezeték köti össze a tengellyel. (Minden más vezető ellenállása és a súrlódás elhanyagolható.)

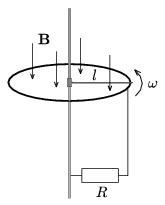
A berendezés homogén, B indukciójú, függőleges mágneses mezőben van. Mekkora erőt kell kifejtenünk a rúd közepénél ahhoz, hogy a rúd állandó $\displaystyle \omega$ szögsebességgel forogjon?

Adatok: R=0,1 k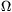, B=0,8 T, l=0,5 m, $\displaystyle \omega$=10 s^-1.

(4 pont)

Közli: Holics László, Budapest

Megoldás.

$\displaystyle F={B^2l^3\omega\over2R}=4\cdot10^{-3}~\rm N.$

P. 3588. U=230 V effektív feszültségű hálózatra sorba kapcsolunk egy 230 ohmos ellenállást, egy ideálisnak tekinthető diódát és egy ampermérőt, amely az áram effektív értékét méri. Mit mutat az ampermérő?

(3 pont)

Közli: Radnai Gyula, Budapest

Megoldás. Az áram effektív értékét a P=RI_eff² egyenlet definiálja, ahol P a műszerre eső teljesítmény. A dióda miatt ez a teljesítmény a szokásos érték fele, így az áram effektív értéke a dióda nélküli eset $\displaystyle \sqrt{2}$-ed része, azaz 0,71 A.

P. 3589. Függőleges falra kör alakú csengőket erősítettek úgy, hogy minden csengő egy képzeletbeli négyzetrács egy-egy rácspontjába került. Ha a falat 10 mm átmérőjű golyókkal dobáljuk, átlagosan minden negyedik esetben szólal meg valamelyik csengő; ha 30 mm-es golyókkal dobálunk, akkor átlagosan minden második esetben találunk el egy csengőt. Feltételezve, hogy a találatok teljesen véletlenszerűek, határozzuk meg a négyzetrács rácsállandóját és a csengők átmérőjét!

(4 pont)

Közli: Bakonyi Gábor, Budapest

Megoldás. Ha a négyzetrács egy éle a, a csengők sugara R, és r₁=10 mm, r₂=30 mm, akkor

$\displaystyle R={r_2-\sqrt{2}r_1\over\sqrt{2}-1}\approx38~{\rm mm}\,,\quad\quad a={2\sqrt{\pi}(r_2-r_1)\over\sqrt{2}-1}\approx17~{\rm cm}\,.$

P. 3590. Az ²³⁸U alfa-bomlását további két, egymás utáni béta-bomlás követi. Mekkora az ²³⁸U ,,dédunokájának'' rendszáma és tömegszáma? Mi az elem neve?

(3 pont)

Jay Orear kérdése, Cornell egyetem (USA)

Megoldás. Urán: $\displaystyle {}^{234}_{\phantom{0}92}$U.