A 2003. februári C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C.705. Egy könyv oldalszámozása az ötödik oldalon kezdődik. Ezen az oldalon az 5-ös szám szerepel. A könyvben még két olyan oldal található, amelyre az első négy oldalhoz hasonlóan nem nyomtatták rá az oldalszámot. A könyvben lévő oldalszámok összege 23 862. Hány oldalas a könyv?

Megoldás: Ha n oldalú a könyv, és az a. ill. a b. oldal nincs megszámozva, akkor

$\displaystyle 23862={n(n+1)\over2}-(1+2+3+4)-(a+b).$

A legkisebb olyan n, amelyre a jobboldal nagyobb lehet, mint a baloldal, a 218 ($\displaystyle \sqrt{2\cdot23862}\approx218,46$). Ekkor azonban a+b=-1 lenne, ami lehetetlen. Egy lapnak két oldala van, tehát n csak páros lehet. n=222 esetén a+b>222. Tehát a könyv 220 oldalas.

C.706. Mely a és b természetes számokra teljesülnek a 90<a+b<100 és a $\displaystyle 0{,}9<\frac{a}{b}<0{,}91$ feltételek?

Megoldás: 0,9<a/b<0,91, azaz 90b<100a<91b. A baloldalból 0<100a-90b, ugyanakkor az első egyenlőtlenség baloldalából 0<90a+90b-8100. A kettőt összeadva 0<190a-8100, tehát 43$\displaystyle le$a.

A jobboldalból 100a-91b<0, ill. 91a+91b-9100<0, és így 191a<9100, tehát a$\displaystyle le$47. Vagyis 43$\displaystyle le$a$\displaystyle le$47. A második egyenlőtlenségből \(\displaystyle {a\over0,91}a=43, akkor ebből (figyelembe véve, hogy b egész 48$\displaystyle le$b$\displaystyle le$47 következik, ami lehetetlen. Ha a=44, akkor 49$\displaystyle le$b$\displaystyle le$48, ez sem lehetséges. Ha a=45, akkor 50$\displaystyle le$b<50, ilyen b sincs. Ha a=46, akkor 51$\displaystyle le$b$\displaystyle le$51. Végül, ha a=47, akkor 542$\displaystyle le$b$\displaystyle le$52. Tehát a megoldások: a₁=46, b₁=51; a₂=47, b₂=52.

C.707. Egy háromszög két oldalával párhuzamosan rajzoljuk meg azokat az egyeneseket, amelyek felezik a háromszög területét. Milyen arányban osztja a háromszög területét a metszéspontjukon keresztül a háromszög harmadik oldalával párhuzamosan húzott egyenes?

Megoldás:

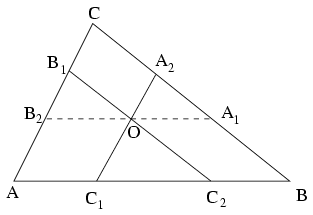
Legyen az ABC háromszög AC oldalával húzott párhuzamos C₁A₂, a BC oldallal húzott párhuzamos pedig C₂B₁, a kettő metszéspontja O, valamint legyen a harmadikként behúzott párhuzamos B₂A₁. Mivel C₁A₂B területe fele ABC területének, azért $\displaystyle {C_1B\over AB}={1\over\sqrt2}$, ebből $\displaystyle C_1B={1\over\sqrt2}AB$. Ugyanígy $\displaystyle {AC_2\over AB}={1\over\sqrt2}$, és így $\displaystyle AC_2={1\over\sqrt2}AB$.

Mivel $\displaystyle AC\parallel C_1A_2$ és $\displaystyle B_2A_1\parallel AB$, azért B₂O=AC₁. Hasonló okok miatt OA₁=C₂B. Így $\displaystyle B_2A_1=AC_1+C_2B=(AB-C_1B)+(AB-AC_2)=(AB-{1\over\sqrt2}AB)+(AB-{1\over\sqrt2}AB)=(2-\sqrt2)AB$.

Tehát $\displaystyle {T_{B_2A_1C}\over T_{ABC}}=(2-\sqrt2)^2\approx0,343$.

C.708. Egy egyenlő szárú háromszög szögei $\displaystyle \alpha$, $\displaystyle \beta$, $\displaystyle \gamma$. Mekkorák ezek a szögek, ha sin²$\displaystyle \alpha$+sin²$\displaystyle \beta$=sin $\displaystyle \gamma$?

Megoldás: Első lehetőség: $\displaystyle alpha$=$\displaystyle beta$. Ekkor $\displaystyle gamma$=180^o-2$\displaystyle alpha$, ahonnan sin$\displaystyle gamma$=sin(180^o-2$\displaystyle alpha$)=sin2$\displaystyle alpha$=2sin$\displaystyle alpha$cos$\displaystyle alpha$, tehát 2sin²$\displaystyle alpha$=2sin$\displaystyle alpha$cos$\displaystyle alpha$. Mivel sin$\displaystyle alpha$=0 nem megoldás, ezért sin$\displaystyle alpha$=cos$\displaystyle alpha$, és így $\displaystyle alpha$=$\displaystyle beta$=45^o, $\displaystyle gamma$=90^o.

Második lehetőség: $\displaystyle beta$=$\displaystyle gamma$. Ekkor $\displaystyle alpha$=180^o-2$\displaystyle beta$. Ebből sin(180^o-2$\displaystyle beta$)=sin2$\displaystyle beta$=2sin$\displaystyle beta$cos$\displaystyle beta$. Ezt beírva az egyenletbe 4sin²$\displaystyle beta$cos²$\displaystyle beta$+sin²$\displaystyle beta$=sin$\displaystyle beta$. Mivel sin$\displaystyle beta$=0 nem megoldás, azért 4sin$\displaystyle beta$(1-sin²$\displaystyle beta$)+sin$\displaystyle beta$=1, amiből -4sin³$\displaystyle beta$+5sin$\displaystyle beta$-1=(sin$\displaystyle beta$-1)(-4sin²$\displaystyle beta$-4sin$\displaystyle beta$+1)=0. Ha sin$\displaystyle beta$=1, akkor $\displaystyle beta$=90^o, ami nem lehet. Ha a második tényező 0, akkor $\displaystyle \sin\beta={-1\pm\sqrt2\over2}$, ebből csak a $\displaystyle {\sqrt2-1\over2}$ megfelelő érték, és ez valóban megoldás lesz.

Tehát $\displaystyle alpha$₁=$\displaystyle beta$₁=45^o, $\displaystyle gamma$₁=90^o; $\displaystyle \alpha_2=180^{\circ}-2\arcsin{\sqrt2-1\over2}\approx156,094^{\circ}$, $\displaystyle \beta_2=\gamma_2=\arcsin{\sqrt2-1\over2}\approx11,953^{\circ}$

C.709. A jól gömbölyített dobókocka a kocka éleit érintő gömbnek a kockával alkotott közös része. Mekkora a felszíne egy ilyen dobókockának, ha két szemközti lapjának távolsága 2 cm?

Megoldás: A keresett felszín hat körből és a nyolc gömbölyített sarokból áll. A hat kör összterülete: T=6^.1²$\displaystyle pi$=6$\displaystyle pi$.

A gömbölyített részek összfelszínét megkapjuk, ha a gömb felszínéből levonjuk a kockából ,,kilógó'' hat gömbsüveg felszínét.

Vágjuk félbe a gömbölyített dobókockát. Az így kapott keresztmetszet:

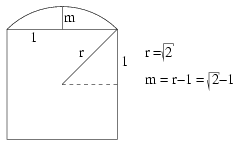
Jelölje A_g a gömb felszínét, A_gs pedig a gömbsüvegek felszínét. Így $\displaystyle A=6\pi+(A_g-6A_{gs})=6\pi+4\pi(\sqrt2)^2-6\cdot2\pi\sqrt2(\sqrt2-1)=(12\sqrt2-10)\pi\approx21,899$ cm².