 |
A 2003 áprilisi A-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 317. Az A={igen,nem} halmazon értelmezett f:An\(\displaystyle \to\)A függvényt döntési függvénynek mondjuk, ha
(a) mindegyik argumentumát megváltoztatva a függvényérték is megváltozik,
valamint
(b) tetszőlegesen választott argumentuma helyébe a függvényértéket helyettesítve a függvényérték nem változik meg.
Egy h: An\(\displaystyle \to\)A függvényt hatalmi függvénynek nevezünk, ha van olyan i index, hogy a függvény értéke mindig az i-edik argumentummal egyezik meg.
Azt az m: A3\(\displaystyle \to\)A függvényt, amelynek értéke mindig az, ami az argumentumok között legalább kétszer fellép, nevezzük demokratikus függvénynek.
Mutassuk meg, hogy minden döntési függvény előállítható hatalmi és demokratikus függvényekből összetett függvényként.
Schweitzer Miklós Matematikai Emlékverseny, 2002
Megoldás. Az állítást indukcióval igazoljuk. Az n=1 és n=2 esetekben minden döntési függvény hatalmi függvény. Legyen tehát n\(\displaystyle \ge\)3, és tegyük fel, hogy kisebb n-ekre az állítás igaz.
Legyen f:An\(\displaystyle \to\)A egy tetszőleges döntési függvény. Definiáljuk a
g1(x1,...,xn)=f(x1,x1,x3,x4,...,xn),
g2(x1,...,xn)=f(x1,x2,x2,x4,...,xn),
g3(x1,...,xn)=f(x3,x2,x3,x4,...,xn)
függvényeket. Ezek valójában n-1 változós döntési függvények, tehát az indukciós feltevés alapján előállíthatók hatalmi és demokratikus függvények kombinációjaként. Az x1,x2,x3 értékeinek diszkutálásával ellenőrizhető, hogy g1,g2,g3 közül legalább kettőnek az értéke megegyezik f értékével, tehát f=m(g1,g2,g3). Ezzel f-et is sikerült a kívánt alakban előállítani.
A. 318. Legyen n tetszőleges pozitív egész szám.
a) Mutassunk példát olyan n-edfokú p polinomra, amelyre bármely x\(\displaystyle \in\)[0,1/2] esetén
\(\displaystyle \left|p(x)-\frac{1}{1-x}\right|<\frac{4}{\big(1+\sqrt2\,\big)^{2n+2}}. \)
b) Bizonyítsuk be, hogy tetszőleges n-edfokú q polinomhoz létezik olyan x\(\displaystyle \in\)[0,1/2] valós szám, amelyre
\(\displaystyle \left|q(x)-\frac{1}{1-x}\right\)\frac{1}{\big(1+\sqrt2\,\big)^{2n+2}}. ">
Megoldás. A baloldalon szereplő kifejezést közös nevezőre hozva,
\(\displaystyle \left|p(x)-\frac{1}{1-x}\right|= \left|\frac{(x-1)p(x)+1}{1-x}\right|.\)
A nevező, (1-x) értéke mindig \(\displaystyle \frac12\) és 1 közé esik. A számláló, (x-1)p(x)+1 egy (n+1)-edfokú polinom, amelynek értéke az 1-ben 1. Azt kell tehát megvizsgálnunk, hogy egy ilyen tulajdonságú polinom mennyire lehet a [0,1/2] intervallumban egyenletesen kicsi. Van a polinomoknak egy nevezetes sorozata, amelyek a [-1,1] intervallumban egyenletesen kicsi értékeket vesznek fel; ezek a Csebisev-polinomok. A kívánt (x-1)p(x)+1 polinomot az (n+1)-edik Csebisev polinomból alkalmas koordináta-transzformációval fogjuk kapni.
Legyen Tn az n-edik Csebisev-polinom (az a polinom, amelyre tetszőleges t valós szám esetén cos nt=Tn(cos t), illetve ch nt=Tn(ch t)), és legyen Rn(x)=Tn(4x-1). Ha x\(\displaystyle \in\)[0,1/2] tetszőleges valós szám, akkor |4x-1|\(\displaystyle \le\)1 és ezért |Rn(x)|\(\displaystyle \le\)1; továbbá Rn(1)=Tn(3). Most megbecsüljük Tn(3) értékét.
Legyen \(\displaystyle a=3+2\sqrt2=\big(1+\sqrt2\big)^2\); erre a számra teljesül, hogy \(\displaystyle 3=\frac{a+1/a}2\), továbbá
\(\displaystyle T_n(3)=\frac{a^n+a^{-n}}2=\frac12\left( \big(1+\sqrt2\big)^{2n}+\big(1+\sqrt2\big)^{-2n}\right),\)
végül
\(\displaystyle \frac12\big(1+\sqrt2\big)^{2n} a) Legyen \(\displaystyle p(x)=\frac{\displaystyle\frac{R_{n+1}(x)}{T_{n+1}(3)}-1}{x-1}.\) Ez valóban polinom, mert a számláló értéke x=1 esetén 0. A foka pontosan n, mert a számláló (n+1)-edfokú. Ha x\(\displaystyle \in\)[0,1/2], akkor \(\displaystyle \left|p(x)-\frac{1}{1-x}\right|=
\frac{|R_{n+1}(x)|}{(1-x)T_n(3)}<
\frac1{\frac12\cdot\frac12\big(1+\sqrt2\big)^{2n+2}}=
\frac4{\big(1+\sqrt2\big)^{2n+2}}.\) A p polinom tehát eleget tesz a feltételeknek. b) A bizonyításhoz szükség lesz az imént definiált p polinom még egy fontos tulajdonságára. Definiáljuk az u0,u1,...,un+1 pontokat a következőképpen: \(\displaystyle u_i=\frac{1+\cos\displaystyle\frac{i\pi}{n+1}}4\quad(i=0,1,\dots,n+1).\) Ezekre a pontokra igaz, hogy \(\displaystyle \frac12=u_\)u_1>\dots>u_{n+1}\ge0">, \(\displaystyle p(u_{2i})-\frac1{1-u_{2i}}=\frac{-R_{n+1}(u_{2i})}{(1-u_{2i})T_{n+1}(3)}=\) \(\displaystyle =\frac{-T_{n+1}\left(\cos\displaystyle\frac{2i\pi}{n+1}\right)}{(1-u_{2i})T_{n+1}(3)}=
\frac{-1}{(1-u_{2i})T_{n+1}(3)}<\frac{-1}{(1+\sqrt2)^{2n+2}},\) és hasonlóan \(\displaystyle p(u_{2i+1})-\frac1{1-u_{2i+1}}=\frac1{(1-u_{2i+1})T_{n+1}(3)\)
\frac1{(1+\sqrt2)^{2n+2}}."> Tegyük most fel, hogy van olyan legfeljebb n-edfokú q polinom, amelyre tetszőleges x\(\displaystyle \in\)[0,1/2] esetén \(\displaystyle \left|q(x)-\frac{1}{1-x}\right|\le\frac{1}{\big(1+\sqrt2\,\big)^{2n+2}}\), és vizsgáljuk a \(\displaystyle d(x)=p(x)-q(x)=
\left(p(x)-\frac1{1-x}\right)-\left(q(x)-\frac1{1-x}\right)\) polinomot. Az u0,...,un+1 pontokban az \(\displaystyle \left(p(x)-\frac1{1-x}\right)\) tag abszolút értéke nagyobb a \(\displaystyle \left(q(x)-\frac1{1-x}\right)\) tag abszolút értékénél, ezért d(x) előjele megegyezik \(\displaystyle \left(p(x)-\frac1{1-x}\right)\) előjelével. Az d(x) polinom értéke tehát az u0,u1,...,un+1 pontokban váltakozva pozitív és negatív. A polinomnak ezért az (u1,u0), (u2,u1), (un+1,un) intervallumok mindegyikében van gyöke. Ez azonban ellentmondás, mert d(x) foka legfeljebb n, ezért legfeljebb csak n gyöke lehet.
A. 319. Létezik-e olyan valós számokból álló a1,a2,... sorozat, amelyre tetszőleges k pozitív egész esetén a \(\displaystyle \sum_{n=1}^\infty a_n^{4k-3}\) sor konvergens, a \(\displaystyle \sum_{n=1}^\infty a_n^{4k-1}\) sor pedig divergens?
Megoldás. A feladat állításánál egy általánosabb tételt bizonyítunk be.
Tétel. Bontsuk fel a pozitív páratlan számok halmazát tetszőleges módon két diszjunkt halmazra, az \(\displaystyle \cal A\) és \(\displaystyle \cal B\) halmazokra. Ekkor létezik olyan valós számokból álló a1,a2,... sorozat, amelyre bármely \(\displaystyle k\in{\cal A}\) esetén a \(\displaystyle \sum a_i^k\) sor konvergens, \(\displaystyle k\in{\cal B}\) esetén pedig divergens.
Az \(\displaystyle {\cal A}=\{1,5,9,\dots\}\), \(\displaystyle {\cal B}=\{3,7,11,\dots\}\) speciális esetben kapjuk a feladat állítását.
A bizonyítások egyszerűbb leírása érdekében bevezetjük még az \(\displaystyle {\cal A}_n={\cal A}\cap\{1,2,\dots,n\}\) és \(\displaystyle {\cal B}_n={\cal B}\cap\{1,2,\dots,n\}\) jelöléseket is.
A tétel bizonyításához szükségünk lesz a következő lemmákra.
1. lemma. Tetszőleges N pozitív egészhez létezik olyan véges hosszúságú, valós számokból álló A=(a1,...,an) sorozat, amelyre \(\displaystyle k\in{\cal A}_N\) esetén \(\displaystyle \sum_{i=1}^na_i^k=0\), \(\displaystyle k\in{\cal B}\) esetén pedig \(\displaystyle \sum_{i=1}^na_i^k\ne0\).
Az 1. lemma bizonyítása. A lemmát N szerinti indukcióval bizonyítjuk. Ha N=0, akkor az egyelemű A=(1) sorozat megfelelő. Legyen most N\(\displaystyle \ge\)1, és tegyük fel, hogy N kisebb értékeire az állítás teljesül; legyen B=(b1,...,bm) egy olyan sorozat, amelyre \(\displaystyle k\in{\cal A}_{N-1}\) esetén \(\displaystyle \sum_{i=1}^mb_i^k=0\), ha pedig \(\displaystyle k\in{\cal B}\), akkor \(\displaystyle \sum_{i=1}^mb_i^k\ne0\).
Ha \(\displaystyle N\not\in{\cal A}_N\), akkor \(\displaystyle {\cal A}_N={\cal A}_{N-1}\), és a B sorozat eleget tesz a lemma feltételeinek. A továbbiakban tehát feltételezhetjük, hogy \(\displaystyle N\in{\cal A}_N\). A kívánt sorozatot a következőképpen kapjuk: 2N-szer felsoroljuk a B sorozat mindegyik elemét, és egyszer-egyszer felsoroljuk az elemek (-2)-szeresét. Formálisan: a sorozat hossza n=(2N+1)m, elemei a következők:
\(\displaystyle a_1=a_2=\dots=a_{2^N}=b_1,\)
\(\displaystyle a_{2^N+1}=a_{2^N+2}=\dots=a_{2\cdot2^N}=b_2,\)
...
\(\displaystyle a_{(m-1)\cdot2^N+1}=a_{(m-1)\cdot2^N+2}=\dots=a_{m\cdot2^N}=b_m,\)
\(\displaystyle a_{m\cdot2^N+i}=-2b_i\quad(i=1,2,\dots,m).\)
Ezzel a választással tetszőleges k páratlan pozitív egész esetén
\(\displaystyle \sum_{i=1}^na_i^k=2^N\sum_{i=1}^mb_i^k+\sum_{i=1}^m(-2b_i)^k= (2^N-2^k)\sum_{i=1}^mb_i^k.\)
Ha k=N, akkor az első tényező 0. Ha \(\displaystyle k\in{\cal A}_{N-1}\), akkor a második. Ha \(\displaystyle k\in{\cal B}\), akkor egyik tényező sem 0. Ezzel az első lemmát igazoltuk.
2. lemma. Tetszőleges N páratlan pozitív egészhez és 0<\(\displaystyle \varepsilon\) 1 valós számhoz létezik olyan véges hosszúságú A=(a1,...,an) sorozat, amelyre a következők teljesülnek:
1 valós számhoz létezik olyan véges hosszúságú A=(a1,...,an) sorozat, amelyre a következők teljesülnek:
a) Ha 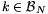 , akkor
, akkor 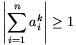 .
.
b) Ha 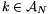 , akkor
, akkor 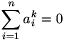 .
.
c) Ha 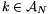 , akkor tetszőleges j
, akkor tetszőleges j n esetén
n esetén 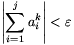 .
.
A 2. lemma bizonyítása. Tekintsük azt a sorozatot, amit az 1. lemma az 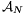 halmazhoz előállít. A sorozat elemeit szorozuk meg egy kellően kicsi számmal; így elérhetjük, hogy az elemek abszolút értékének összege
halmazhoz előállít. A sorozat elemeit szorozuk meg egy kellően kicsi számmal; így elérhetjük, hogy az elemek abszolút értékének összege  -nál kisebb legyen. Az így kapott sorozat legyen
-nál kisebb legyen. Az így kapott sorozat legyen 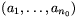 .
.
Az A halmazt úgy kapjuk, hogy a B sorozatot többször, n1-szer egymás után írjuk. Tehát n=n0.n1, 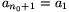 ,
, 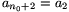 , ...,
, ...,  . Ekkor tetszőleges k esetén
. Ekkor tetszőleges k esetén
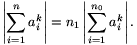
Ha 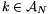 , akkor a második tényező 0, ezért a b) tulajdonság igaz. Ha
, akkor a második tényező 0, ezért a b) tulajdonság igaz. Ha 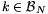 , akkor a második tényező nem 0. Ha n1-et elegendően nagynak választjuk, akkor a szorzat nagyobb lesz 1-nél. Mivel
, akkor a második tényező nem 0. Ha n1-et elegendően nagynak választjuk, akkor a szorzat nagyobb lesz 1-nél. Mivel 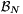 véges halmaz, az n1-et tudjuk úgy választani, hogy
véges halmaz, az n1-et tudjuk úgy választani, hogy 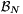 mindegyik eleméhez ,,elég nagy'' legyen. Az n1-et tehát lehetséges úgy megválasztani, hogy az a) tulajdonság is teljesüljön.
mindegyik eleméhez ,,elég nagy'' legyen. Az n1-et tehát lehetséges úgy megválasztani, hogy az a) tulajdonság is teljesüljön.
Ha 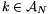 és j=j0n0+j1, ahol 0
és j=j0n0+j1, ahol 0 j1<n0, akkor
j1<n0, akkor
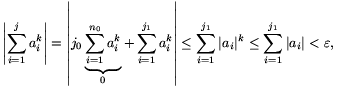
vagyis a c) fetétel is teljesül.
A tétel bizonyítása. Legyen tetszőleges m pozitív egészre  egy olyan véges hosszúságú számsorozat, amit a 2. lemma elállít az N=m és az
egy olyan véges hosszúságú számsorozat, amit a 2. lemma elállít az N=m és az 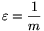 számokhoz. Az így kapott sorozatokat írjuk egymás után:
számokhoz. Az így kapott sorozatokat írjuk egymás után:
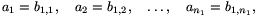
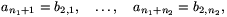
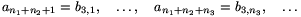
Azt állítjuk, hogy erre sorozatra teljesülnek a feladat feltételei., azaz  esetén a
esetén a 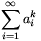 sor konvergens,
sor konvergens, 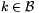 esetén pedig divergens.
esetén pedig divergens.
Legyen először 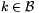 . Mivel tetszőleges j pozitív egészre
. Mivel tetszőleges j pozitív egészre
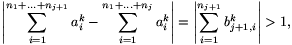
a 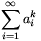 sor divergens.
sor divergens.
Legyen most  és
és 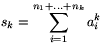 . Megmutatjuk, hogy ez a szám a sor határértéke. Legyen N>n1+...+nk egy tetszőleges pozitív egész, legyen j az az index, amelyre n1+...+nj<N
. Megmutatjuk, hogy ez a szám a sor határértéke. Legyen N>n1+...+nk egy tetszőleges pozitív egész, legyen j az az index, amelyre n1+...+nj<N n1+...+nj+1 és M=N-(n1+...+nj). Ekkor
n1+...+nj+1 és M=N-(n1+...+nj). Ekkor
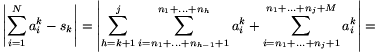

A N növekedésével  , tehát
, tehát 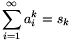 .
.

