A 2003 szeptemberi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 323. Az ABC háromszög izogonális pontja I (az a pont a háromszög belsejében, amelyre AIB\(\displaystyle \angle\)=BIC\(\displaystyle \angle\)=CIA\(\displaystyle \angle\)=120^o). Bizonyítsuk be, hogy az ABI, BCI és CAI háromszögek Euler-egyenesei egy ponton mennek át.

1. megoldás (Rácz Béla András, Budapest). Megmutatjuk, hogy mindhárom Euler-egyenes átmegy az ABC háromszög súlypontján. A szimmetria miatt elég ezt a BCI háromszög Euler-egyenesére igazolni.

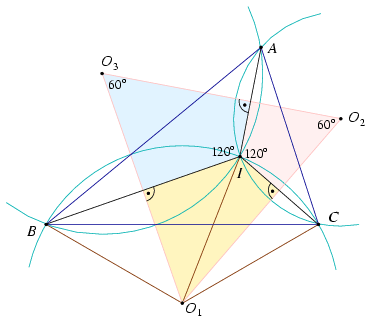
1. ábra

Rajzoljunk a BC oldalra kifelé egy szabályos háromszöget, ennek harmadik csúcsa legyen A', középpontja O₁. Az IBA'C négyszög húrnégyszög, mert BA'C\(\displaystyle \angle\)+CIB\(\displaystyle \angle\)=60^o+120^o=180^o. Mivel A'B=A'C, az A'I szakasz szögfelező a CIB szögben. Ebből következik, hogy A, I és A' egy egyenesen van (1. ábra).

Legyen a BC szakasz felezőponta F, az ABC háromszög súlypontja S, a BCI háromszög súlypontja S₁. Mivel S, S₁ és O₁ nem más, mint az AF, IF, illetve A'F szakaszok F-hez közelebbi harmadolópontja, az S, S₁ és O₁ pontok is egy egyenesen vannak. Más szóval, a BCI szakasz Euler egyenese, O₁S₁ átmegy az S ponton.

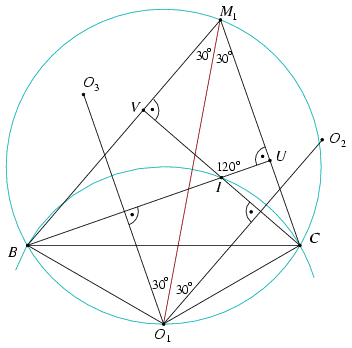
2. megoldás. Legyen a BCI, CAI, ABI háromszögek körülírt körének középpontja rendre O₁, O₂, O₃, magasságpontjaik M₁, M₂, illetve M₃. Az O₁O₂, O₂O₃, O₃O₁ egyenesek éppen a CI, AI, illetve BI szakaszok felező merőlegesei, és a besatírozott négyszögek szögeinek összeszámolásából kapjuk, hogy az O₁O₂O₃ háromszög mindegyik szöge 60^o, az O₁O₂O₃ háromszög szabályos (2. ábra).

2. ábra

Megmutatjuk, hogy az ABI, BCI és CAI háromszögek Euler-egyenesei mind átmennek az O₁O₂O₃ háromszög középpontján. A szimmetria miatt elég ezt az egyik háromszögre igazolni; vizsgáljuk tehát a BCI háromszöget. Mivel BO₁=IO₁=CO₁, az O₁O₂ és O₁O₃ egyenesek szögfelezők a BO₁I és IO₁C szögekben, ezért BO₁C\(\displaystyle \angle\)=2O₃O₁O₂\(\displaystyle \angle\)=2^.60^o=120^o.

3. ábra

Jelöljük a BI és CM₁ egyenesek metszéspontját U-val, CI és BM₁ metszéspontját V-vel. Az M₁VIU négyszög szögeinek összeszámolásából CM₁B\(\displaystyle \angle\)=60^o. az M₁BO₁C négyszög húrnégyszög, mert CM₁B\(\displaystyle \angle\)+BO₁C\(\displaystyle \angle\)=60^o+120^o=180^o. Mivel pedig BO₁=O₁C, az is igaz, hogy CM₁O₁\(\displaystyle \angle\)=O₁M₁B\(\displaystyle \angle\)=30^o.

Végül, az M₁O₁O₂ és O₁M₁B szögek, valamint az O₃O₁M₁ és CM₁O₁ szögek váltószögek, ezért M₁O₁O₂\(\displaystyle \angle\)=O₃O₁M₁\(\displaystyle \angle\)=30^o. A BCI háromszög Euler-egyenese, O₁M₁ tehát nem más, mint az O₃O₁O₂ szög felezője, ami átmegy az O₁O₂O₃ háromszög középpontján.

A. 324. Igazoljuk, hogy tetszőleges a, b, c pozitív valós számok esetén

\(\displaystyle \frac{1}{a(1+b)}+\frac{1}{b(1+c)}+\frac{1}{c(1+a)}\ge\frac{3}{1+abc}. \)

1. megoldás. Beszorozva és átrendezve az egyenlőtlenség a következő alakra hozható:

ab(b+1)(ca-1)²+bc(c+1)(ab-1)²+ca(a+1)(bc-1)²\(\displaystyle \ge\)0.

2. megoldás (Birkner Tamás, Budapest). Szorozzuk meg az egyenlőtlenséget (1+abc)-vel, adjunk hozzá mindkét oldalhoz 3-at, és rendezzük át a következőképpen:

\(\displaystyle \left({1+abc\over a(1+b)}+1\right)+ \left({1+abc\over b(1+c)}+1\right)+ \left({1+abc\over c(1+a)}+1\right) \ge6\)

\(\displaystyle \left({1+a\over a(1+b)}+{b(1+c)\over1+b}\right)+ \left({1+b\over b(1+c)}+{c(1+a)\over1+c}\right)+ \left({1+c\over c(1+a)}+{a(1+b)\over1+a}\right)\ge6\)

\(\displaystyle \left({1+a\over a(1+b)}+{a(1+b)\over1+a}\right)+ \left({1+b\over b(1+c)}+{b(1+c)\over1+b}\right)+ \left({1+c\over c(1+a)}+{c(1+a)\over1+c}\right)\ge6.\)

Az utolsó sorban mindegyik zárójelben \(\displaystyle x+{1\over x}\) alakú kifejezés áll, tehát mindegyik legalább 2.

3. megoldás (Dobrovolska Galyna, Kiev). Beszorozva (1+abc)-vel és átrendezve,

\(\displaystyle {1\over a(1+b)}+{abc\over a(1+b)}+ {1\over b(1+c)}+{abc\over b(1+c)}+ {1\over c(1+a)}+{abc\over c(1+a)}\ge3\)

\(\displaystyle {1\over a(1+b)}+{ab\over1+a}+ {1\over b(1+c)}+{bc\over1+b}+ {1\over c(1+a)}+{ca\over1+c}\ge3\)

\(\displaystyle {1\over a}\cdot{1\over1+b}+b\cdot{1\over{1+{1\over a}}}+ {1\over b}\cdot{1\over1+c}+c\cdot{1\over{1+{1\over b}}}+ {1\over c}\cdot{1\over1+a}+a\cdot{1\over{1+{1\over c}}}\ge6. \eqno(1)\)

Mivel az \(\displaystyle {1\over a}\) és b számok ellentétesen rendezettek, mint az \(\displaystyle {1\over1+{1\over a}}\) és \(\displaystyle {1\over1+b}\) számok,

\(\displaystyle {1\over a}\cdot{1\over1+b}+b\cdot{1\over{1+{1\over a}}} \ge{1\over a}\cdot{1\over{1+{1\over a}}}+b\cdot{1\over1+b} ={1\over1+a}+{b\over1+b}. \eqno(2)\)

Hasonlóan kapjuk, hogy

\(\displaystyle {1\over b}\cdot{1\over1+c}+c\cdot{1\over{1+{1\over b}}} \ge{1\over1+b}+{c\over1+c},\eqno(3)\)

illetve

\(\displaystyle {1\over c}\cdot{1\over1+a}+a\cdot{1\over{1+{1\over c}}} \ge{1\over1+c}+{a\over1+a}.\eqno(4)\)

A (2), (3) és (4) egyenlőtlenségeket összeadva (1)-et kapjuk.

A. 325. Egy n-elemű A halmaznak kiválasztottuk néhány 4-elemű részhalmazát úgy, hogy bármelyik két kiválasztott négyesnek legfeljebb két közös eleme van. Bizonyítsuk be, hogy A-nak létezik olyan legalább \(\displaystyle \root3\of{6n}\) elemű részhalmaza, amelynek egyik négyes sem része.

Megoldás. Legyen N a kiválasztott 4-elemű részhalmazok halmaza. Feltételezzük, hogy N\(\displaystyle \ne\)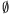 és n4 (Ha pl. n2 és egyetlen négyes sincs, akkor a feladat állítása nyilván nem igaz, mert .)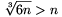

Nevezzünk A egy részhalmazát ,,jónak'', ha N egyik elemét sem tartalmazza. Triviálisan jók például a legfeljebb 3-elemű halmazok, beleértve az üres halmazt is. Egy jó halmazt nevezzünk ,,maximálisnak'', ha nincs nála bővebb jó halmaz, vagyis akárhogyan veszünk is a halmazhoz egy újabb elemet, azzal együtt már nem jó halmaz. Legalább egy maximális jó halmaz biztosan létezik, mert egy tetszőleges jó részhalmazból kiindulva egyesével hozzáadhatunk új elemeket mindaddig, amíg ez lehetséges.

Bebizonyítjuk, hogy mindegyik maximális jó halmaznak több eleme van, mint 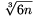, vagyis a feladat követelményeinek bármelyik maximális jó részhalmaz eleget tesz.

Legyen M egy tetszőleges maximális jó halmaz, |M|=k. Nyilván k3, mert minden 3-elemű halmaz jó. Ha 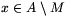egy tetszőleges M-en kívüli elem, akkor M{x} már nem jó halmaz, mert M maximális. Ez csak úgy lehet, ha az x elem az M halmaz valamelyik három elemével együtt egy N-beli négyest alkot. Minden egyes 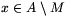esetén jelöljük az egyik ilyen elemhármast h(x)-szel.

Ha 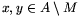két különböző elem, akkor a H₁=h(x){x} és H₂=h(y){y} halmazok is N-beliek. A H₁ és H₂ négyesek különbözők, mert például xH₁, de 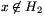. Mivel pedig különbözők, legfeljebb két közös elemük lehet. Ebből következik, hogy h(x)h(y).

Tekintsük most az összes h(x) halmazt. Ez összesen n-k különböző, 3-elemű részhalmaza M-nek. Mivel M-nek összesen 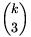3-elemű részhalmaza van, ebből következik, hogy . Ebből a becslésből kapjuk az állítást:

6nk³-3k²+8k=k³-k(3k-8)<k³