A 2003. decemberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3682.Két pozitív egész, a és b legnagyobb közös osztójának és legkisebb közös többszörösének az összege egyenlő (a+b)-vel. Bizonyítsuk be, hogy ekkor az a és b számok közül valamelyik osztható a másikkal.

(3 pont)

Megoldás: Legyen a=da' és b=db', ahol d=(a,b) az a és b számok legnagyobb közös osztója. Ekkor az a és b számok legkisebb közös többszöröse, [a,b]=ab/d=da'b'. A feladat feltétele alapján

d+da'b'=(a,b)+[a,b]=a+b=da'+db',

ahonnan d-vel történő egyszerűsítés és átrendezés után a'b'-a'-b'+1=0 adódik. A baloldalt szorzattá alakítva (a'-1)(b'-1)=0, tehát vagy a'=1, a=d, mely esetben b osztható a-val, vagy pedig b'=1, b=d, amikor is a osztható b-vel.

B.3683.Melyek azok a szabályos sokszögek, amelyek hézag és átfedés nélkül összerakhatók más, ugyanolyan oldalhosszúságú szabályos sokszögekből?

(4 pont)

XII. Nemzetközi Magyar Matematikaverseny, 2003

Megoldás: Mivel egy n-szög szögeinek összege (n-2)180^o, egy szabályos n-szög minden szöge $\displaystyle (1-{2\over n})180^\circ$. Nem teljesen egyértelmű a feladat szövegéből, hogy az összerakásban szereplő sokszögek oldalai csak egymás közt egyforma hosszúak, vagy az eredetivel is megegyező hosszú oldalakkal rendelkeznek, ezért az első, általánosabb feladatot oldjuk meg. Ha van olyan sokszög a kirakásban, melynek egy w csúcsa az eredeti S sokszög valamelyik oldalának belső pontja, akkor azon sokszögek, melyeknek w is csúcsa, w-nél lévő szögeit összeadva éppen 180^o-ot kell kapnunk. Ez csak úgy lehetséges, ha három szabályos háromszöget, két négyzetet, vagy pedig egy szabályos háromszöget és egy szabályos hatszöget illesztünk egymás mellé. (7 vagy több oldalú sokszög nem szerepelhet itt, mert amellett 60^o-nál kisebb szög maradna, ahová már egyetlen további sokszög sem illeszthető be átfedés nélkül, ötszög esetén pedig 72^o-os szög maradna ki, ahová átfedés nélkül már csak egy háromszög illeszthető be, de akkor a megmaradt 12^o-os szöggel már végképp nem tudunk mit kezdeni.)

Ha most S valamely v csúcsához a kirakásban csak egyetlen S' sokszög illeszkedik, akkor szükségképpen S' hasonló S-hez, de nem egybevágó vele, így S' v-vel szomszédos csúcsaira alkalmazhatjuk az előbbi észrevételt, vagyis ekkor S', és ennek következtében S is, csakis háromszög, négyszög vagy hatszög lehet. Ezekben az esetekben ez elő is fordulhat: a szabályos háromszöget középvonalaival 4 egybevágó szabályos háromszögre bonthatjuk, a négyzet is felbontható négy egybevágó négyzetre, végül a hatszöget három egybevágó hatszögből és hat ezekkel megegyező oldalú szabályos háromszögből rakhatjuk össze. (Ez utóbbi észrevétünkre igazából nincs szükség, hiszen a szabályos hatszöget nyilván felbonthatjuk 6 egybevágó szabályos háromszögre is, és ezek oldala a hatszög oldalaival is megegyező hosszúságú.)

S egy csúcsához kettőnél több sokszög nem illeszkedhet, mert akkor S egy szöge legalább 3^.60^o lenne. Marad tehát annak a vizsgálata, amikor S valamely v csúcsához a kirakásban pontosan két sokszög, S₁ és S₂ illeszkedik. Ha e két sokszög egy-egy szögét összeadjuk, 180^o-nál kisebb szöget kell kapnunk, ami csak úgy lehetséges, ha az egyik sokszög, mondjuk S₁, háromszög, a másiknak pedig legfeljebb 5 oldala van. Ha S₂ is háromszög, akkor S hatszög, ezt az esetet már megvizsgáltuk. Ha S₂ négyzet, akkor S egy szöge 150^o, vagyis S szabályos 12-szög. Ezt kirakhatjuk úgy, hogy oldalaira befelé felváltva négyzeteket és szabályos háromszögeket illesztünk, a kimaradó szabályos hatszöget pedig 6 szabályos háromszögre bontjuk. Végül, ha S₂ ötszög, akkor S egy szöge 168^o, vagyis S szabályos 30-szög. Ez azonban nem lehetséges. Ekkor ugyanis a megoldás elején említett okok miatt S₂ és S ugyanolyan oldalhosszúságú kell, legyen. S₂ és S közös oldalának másik u csúcsánál S₂ mellé egy újabb szabályos háromszögnek kell illeszkednie. S-nek u után következő t csúcsához ismét egy háromszög és egy S₃ ötszög illeszkedik. Mivel az ötszög oldala ut nem lehet, S₂ és S₃ egy közös p csúcsukban érintik egymást úgy, hogy az utp háromszög szabályos. A p pont körül az S₂ és S₃ ötszögek pu illetve pt oldalától különböző oldalai által bezárt 360^o-60^o-2^.108^o=84^o-os tartományba kellene most további szabályos sokszögeket illesztenünk, ami nyilván lehetetlen.

Összefoglalva, ha a feladatot a szűkebb értelmezésben vizsgáljuk, akkor megoldásként a szabályos hatszöget és a szabályos 12-szöget kapjuk, a tágabb értelmezésben a szabályos háromszög és a négyzet is megoldása a feladatnak.

B.3684.Szerkeszünk háromszöget, ha adott két oldala, a és b, továbbá tudjuk, hogy (a szokásos jelölésekkel) $\displaystyle \alpha$=3$\displaystyle \beta$.

(3 pont)

Megoldás. Induljunk ki a kész ábrából és használjuk annak jelöléseit. Legyen K a BC oldalnak az a belső pontja, amelyre KAB$\displaystyle \angle$= $\displaystyle \beta$. Ekkor az ABK háromszög egyenlő szárú, hiszen az AB oldalon fekvő mindkét szöge $\displaystyle \beta$. Emiatt AK= KB. A CAK szög nyilván $\displaystyle \alpha$-$\displaystyle \beta$, és mivel $\displaystyle \alpha$= 3$\displaystyle \beta$, azért CAK$\displaystyle \angle$= $\displaystyle \alpha$-$\displaystyle \beta$= 3$\displaystyle \beta$-$\displaystyle \beta$= 2$\displaystyle \beta$. Az AKC szög az AKB háromszög egyik külső szöge, így egyenlő a két nem mellette fekvő belső szög összegével: AKC$\displaystyle \angle$= $\displaystyle \beta$+$\displaystyle \beta$= 2$\displaystyle \beta$. Ezért az AKC háromszög is egyenlő szárú, hiszen az AK oldalon fekvő mindkét szöge 2$\displaystyle \beta$. Emiatt CK= AC=b, tehát AK=KB=CB-CK=a-b.

Az AKC háromszög mindhárom oldalát ismerjük tehát: AC=CK=b, AK=a-b; így három oldalából az AKC háromszög megszerkeszthető, és ebből az ABC háromszög B csúcsa is, ha a CK szakasz K-n túli meghosszabbítására K-ból (a-b)-t mérünk.

A kapott háromszögben AC=b, BC=b+(a-b)=a, végül a fenti okoskodás megfordításával adódik, hogy $\displaystyle \alpha$=3$\displaystyle \beta$.

Mivel $\displaystyle \alpha$=3$\displaystyle \beta$, azért a>b szükséges, hiszen egy háromszögben nagyobb szöggel szemben nagyobb oldal van. Ekkor a-b pozitív, az a-b nagyságú szakasz megszerkeszthető. A háromszög-egyenlőtlenség szerint

$\displaystyle \begin{array}{l} \,AC+C$AK,\quad\mbox{azaz}\quad b+b>a-b,\quad\mbox{átrendezve:}\quad3b>a,\\[9pt] \left.\begin{array}{@{}l} AC+AK>CK\\[3pt] CK+AK>AC \end{array}\right\}\quad b+(a-b)>b,\quad\mbox{azaz}\quad a>b. \end{array} ">

Ha ezek a feltételek teljesülnek, akkor lényegében egyértelműen adódik az AKC háromszög. A második lépés, a B csúcs szerkesztése ezután ugyancsak egyértelműen elvégezhető.

Ha b<a<3b, akkor pontosan egy megoldása van a feladatnak, ha pedig ez nem teljesül, akkor nem szerkeszthető ilyen ABC háromszög.

Farkas Gergő (Dombóvár, Illyés Gyula Gimn., 10. évf.) dolgozata alapján

B.3685.Egy számítógépes játékban minden egyes játék alkalmával egész pontszámot érhetünk el. A legjobb 30 eredményt számon tartó listán a játék megalkotója egy-egy fantázianév mellett a 30, 29,28,..., 1 pontszámokat tüntette fel. Egy játék során elért eredményünk - saját nevünk alatt - akkor kerül fel a listára, ha pontszámunk nagyobb, mint az aktuális listán szereplő legkisebb pontszám, amely ezután értelemszerűen lekerül a listáról. Egyenlő pontszámok esetén az utoljára felkerült pontszám kerül le a listáról. A besorolás ``alulról'' történik, tehát csak azokat az eredményeket fogjuk megelőzni a listán, amelyeknél nagyobb pontszámot értünk el. Feltéve, hogy minden egyes játék után feljutunk a listára, legalább hány játékot kell lejátszanunk ahhoz, hogy biztosan a mi nevünk szerepeljen a listán valamennyi pontszám mellett?

(4 pont)

Megoldás: Adjuk össze a fantázianevek mellett szereplő helyezési számokat. Helyezési szám alatt azt az 1 és 30 közötti számot értjük, ami megmondja, hogy az eredmény alulról hanyadik helyen áll a listán. Vagyis a legjobb eredmény helyezési száma 30, a leggyengébbé, amelyik tehát a következő játék után lekerül a listáról, pedig 1. Az egyszerűség kedvéért tekintsük a listáról éppen lekerült eredmény helyezési számát 0-nak. Kezdetben ez az összeg 1+2+...+30=465. Azt állítjuk, hogy minden egyes játék után csökkenni fog ez az összeg, egészen addig, amíg 0 nem lesz. Mivel az összeg mindig egész szám, legfeljebb 465 játék után már biztosan 0 lesz az összeg, vagyis már csak a mi nevünk fog szerepelni a listán.

Az állítás igazolásához tegyük fel, hogy egy adott pillanatban az összeg nem 0, tehát még szerepel legalább egy fantázianév a listán. Vegyük észre, hogy ha a listán az 1. helyezési számú eredmény t ponttal szerepel, akkor azok a fantázianevek, melyek mellett t, vagy annál több pont van, még rajta vannak a listán. Játsszunk most le egy játékot, mellyel felkerülünk a listára, mondjuk p ponttal. Ekkor nyilván p>t. Ha ezen játék lejátszása előtt valamely fantázianév mellett legalább p pont szerepelt, akkor annak helyezési száma nem változik meg, ha azonban p-nél kevesebb pont szerepelt mellette, akkor helyezési száma 1-gyel csökken. Elég tehát azt megmutatni, hogy a szóban forgó játék előtt a listán szereplő valamelyik fantázianév mellett kevesebb, mint p pont szerepelt. Ez azonban p>t miatt előző megjegyzésünkből azonnal következik.

Másrészről viszont előfordulhat, hogy csak a 465. játék után kerül le valamenynyi fantázianév a listáról. Hogy ez hogyan fordulhat elő, arra rájöhetünk, ha figyelembe vesszük, hogy ekkor a megoldás első részében bevezetett összegnek minden egyes játék után pontosan 1-gyel kell csökkennie. Nem nehéz ellenőrizni, hogy ha 465 játák során rendre először 2 pontot, azután kétszer egymás után 3 pontot, majd háromszor egymás után 4 pontot, és így tovább, végül 30-szor egymás után 31 pontot érünk el, akkor az utolsó játék lejátszása után fog először bekövetkezni, hogy már csak a saját nevünk alatt szerepel eredmény a listán. Valóban, i szerinti teljes indukcióval könnyen igazolható, hogy ekkor 1$\displaystyle \le$i$\displaystyle \le$29 esetén az első A_i=1+2+...+ i játék lejátszása után az aktuális lista a 30, 29, ...,i+1, i+1, ...,i+1 pontszámokat tartalmazza, az első 30-i eredmény mellett az eredeti fantázianév, az utolsó i eremény mellett pedig a saját nevünk feltüntetésével. Az A₂₉-edik játék után pedig még legalább 30 játék szükséges ahhoz, hogy a listavezető 30-as pontszám is lekerüljön a listáról.

B.3686.Az ABCD tetraéderben az ABD és ACD szögek tompaszögek. Mutassuk meg, hogy ekkor AD>BC.

(3 pont)

Megoldás: Ha az AD oldal felezőpontja F, akkor az ADB síkban az AD átmérőjű kört megrajzolva, a B pont a körvonal belsejébe esik. Ebből következik, hogy FB rövidebb az F középpontú kör r=AF sugaránál. Ugyanígy kapjuk, hogy FC<AF. A BCF háromszög oldalaira a háromszög-egyenlőtlenséget felírva nyerjük a bizonyítandó állítást:

BC<BF+CF<AF+AF=AD.

B.3687.Oldjuk meg a valós számok halmazán az alábbi egyenletet:

$\displaystyle \root5\of{x^3+2x}=\root3\of{x^5-2x}.$

(5 pont)

Megoldás: Az egyenlet nyilván ekvivalens az (x³+2x)³=(x⁵-2x)⁵ egyenlettel. Ez teljesül, ha x=0, egyébként pedig ekvivalens az (y+2)³=y(y²-2)⁵ egyenlettel, ahol y=x²>0. Ezt az egyenletet y=2 nyilván kielégíti, ahonnan az $\displaystyle x=\pm\sqrt{2}$ megoldásokhoz jutunk. A továbbiakban megmutatjuk, hogy más pozitív y szám nem elégítheti ki az egyenletet. Valóban, ha \(\displaystyle 0y+2 és y(y²-2), illetőleg y+2 és (y²-2)² értéke.

Mivel y(y²-2)-(y+2)=y³-3y-2=(y-2)(y+1)², látható, hogy y>2 esetén y(y²-2)>y+2>0, míg $\displaystyle \sqrt{2}\le y<2$ esetén 0$\displaystyle \le$y(y²-2)<(y+2). Ugyanígy (y²-2)²-(y+2)=y⁴-4y²-y+2=(y-2)(y³+2y²-1) alapján világos, hogy y>2 esetén (y²-2)²>y+2>0, míg $\displaystyle \sqrt{2}\le y<2$ esetén 0$\displaystyle \le$y(y²-2)<(y+2), hiszen az y³+2y²-1 kifejezés értéke nyilván pozitív, ha $\displaystyle y\ge\sqrt{2}$.

Fenti megállapításainkat összegezve, y>2 esetén (y+2)³<y(y²-2)⁵, míg 0<y<2 esetén (y+2)³>y(y²-2)⁵. Az (y+2)³=y(y²-2)⁵ egyenletnek a pozitív számok körében tehát y=2 az egyetlen megoldása, az eredeti egyenlet gyökei pedig $\displaystyle -\sqrt{2},0$ és $\displaystyle \sqrt{2}$.

B.3688.Keressünk olyan egész számot, amelynek a négyzetgyökében a tizedesvessző után közvetlenül a 414213462 számjegysorozat áll.

(4 pont)

Holló Gábor (Budapest) javaslata alapján

Megoldás: Ha a keresett N számra $\displaystyle \sqrt{N}$ egész részét K-val, törtrészét pedig $\displaystyle \kappa$-val jelöljük, akkor $\displaystyle \alpha$=0,414213462 esetén a $\displaystyle \kappa$-$\displaystyle \alpha$=$\displaystyle \epsilon$ jelöléssel 0$\displaystyle \le$ $\epsilon$ <10^-9 kell, hogy teljesüljön, és ez nyilván elegendő is. 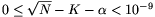Vagyis rögzített K pozitív egész mellett az N egész szám akkor lesz megfelelő, ha egyrészt K²<N<(K+1)², másrészt $0\le\sqrt{N}-K-\alpha<10^{-9}$ teljesül. Ez utóbbi azzal ekvivalens, hogy (K+ $\alpha$ )² $\le$ N<(K+ $\alpha$ +10^-9), vagyis

(K²+2K $\alpha$ )+ $\alpha$ ² $\le$ N<(K²+2K $\alpha$ )+2K10^-9+( $\alpha$ ²+10^-18+2 $\alpha$ 10^-9).

Az ijesztő egyenlőtlenség jobban kezelhető, ha K értékét 10⁹-nel oszthatónak választjuk, hiszen ekkor L=K²+2K $\alpha$ egész szám lesz. Legyen tehát K=10⁹, és vizsgáljuk meg, mit eredményez ez a választás. Ebben az esetben (K²+2K $\alpha$ )+ $\alpha$ ²<L+1, míg

(K²+2K $\alpha$ )+2K10^-9+( $\alpha$ ²+10^-18+2 $\alpha$ 10^-9)>L+2K10^-9=L+2.

Ezek szerint N=L+1 esetén a második feltétel teljesül. Az első feltétel is teljesül, hiszen egyrészt nyilván N>L>K², másrészt N=L+1=K²+2K $\alpha$ +1<K²+2K+1=(K+1)². Az

N=L+1=10¹⁸+2^.10⁹^.0,414213462+1=1000000000828426925

szám tehát mefelelő lesz.

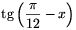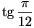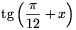B.3689.Keressük meg az összes olyan x valós számot, amelyre $\mathop{\rm tg}\left(\frac{\pi}{12}-x\right)$ , $\mathop{\rm tg} \frac{\pi}{12}$ és $\mathop{\rm tg}\left(\frac{\pi}{12}+x\right)$ (valamilyen sorrendben) egy mértani sorozat három szomszédos tagja.

(4 pont)

Megoldás: Ha a mértani sorozat középső tagja 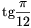$\tan{\pi\over12}$ , akkor

$\tan^2{\pi\over12}=\tan\left({\pi\over12}-x\right) \tan\left({\pi\over12}+x\right)= {\tan{\pi\over12}-\tan x\over1+\tan{\pi\over12}\tan x}\cdot{\tan{\pi\over12}+\tan x\over1-\tan{\pi\over12}\tan x}.$

Innen az $a=\tan^2{\pi\over12}\ne1$ , y=tan²x helyettesítéssel beszorzás után a(1-ay)=a-y, (a²-1)y=0 adódik. Mivel a $\ne$ $\pm$ 1, kapjuk hogy y=0, x=k $\pi$ ahol k tetszőleges egész szám. Ez nyilván jó is és konstans mértani sorozatot eredményez.

Ha a mértani sorozat középső tagja 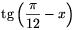$\tan\left({\pi\over12}-x\right)$ , akkor a 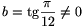$b=\tan{\pi\over12}\ne0$ és z=tan x helyettesítéssel most a

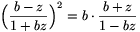
$\Bigl({b-z\over1+bz}\Bigr)^2=b\cdot{b+z\over1-bz}$

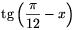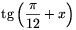egyenletre jutunk, ahol bz $\ne$ $\pm$ 1 a feladatban szereplő $\tan\left({\pi\over12}-x\right)$ és $\tan\left({\pi\over12}+x\right)$ kifejezések értelmezhetőségének szükséges és elégséges feltétele. Ha ez teljesül, akkor ekvivalens átalakításokkal (b-z)²(1-bz)=b(b+z)(1+bz)², vagyis

(b³+b)z³+(b⁴-1)z²+(3b³+3b)z=0.

Ha z=0, akkor az előző részben már megtalált megoldásokhoz jutunk, ellenkező esetben pedig b²+1 $\ne$ 0 miatt z pontosan akkor lesz megoldása az egyenletnek, ha bz²+(b²-1)z+3b=0, vagyis ha

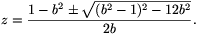
$z={1-b^2\pm\sqrt{(b^2-1)^2-12b^2}\over2b}.$

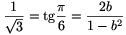Mivel ${1\over\sqrt{3}}=\tan{\pi\over6}={2b\over1-b^2}$ , kapjuk hogy $1-b^2=2\sqrt{3}b$ , (b²-1)²=12b², vagyis a gyökjel alatti szám értéke 0. Ezért most 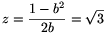$z={1-b^2\over2b}=\sqrt{3}$ , vagyis $x={\pi\over3}+k\pi$ , ahol k tetszőleges egész szám. Lévén $b\ne\pm{1\over\sqrt{3}}$ , ezen x értékek valóban megoldásai az egyenletnek.

Ha a mértani sorozat középső tagja 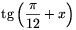$\tan\left({\pi\over12}+x\right)$ , akkor -x értékére kapjuk az előbb említett megoldásokat. A feladat összes megoldása tehát 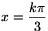$x={k\pi\over3}$ alakban adható meg, ahol k tetszőleges egész szám.

B.3690.Adott az 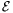$\cal E$ ellipszis nagytengelyének két végpontja, az ellipszis e érintője és azon egy P pont. Szerkesszük meg a P-ből 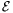$\cal E$ -hez húzható másik érintőt.

(5 pont)

Megoldás: Mivel a fókuszokból az érintőre állított merőlegesek talppontjai a főkörön vannak, ezért - az adott pontokat X-szel és Y-nal jelölve - a szerkesztés menete a következő: Az XY átmérőjű kört megszerkesztve megkapjuk a főkört, ennek és e-nek a metszéspontjaiban e-re merőlegest állítva a merőlegesek és az XY szakasz metszéspontjaiként megkapjuk a két fókuszt, F₁-et és F₂-t. (Akkor kapunk két pontot, ha e metszi a főkört, ebben az esetben erre a két pontra mindig teljesül, hogy XF₁=F₂Y.) Ezután a PF₁ átmérőjű kör és a főkör, illetve a PF₂ átmérőjű kör és a főkör metszéspontját összekötve megkapjuk a másik érintőt.

Ha ezek a körök csak érintik a főkört, akkor P rajta van az ellipszisen, és ezért nem kapunk másik érintőt.

Ha e nem metszi a főkört, akkor nincs megoldás; ha érinti, akkor csak abban az esetben lehet e az ellipszis érintője, ha X-ben vagy Y-ban érinti a főkört. Ekkor viszont P helyzetétől függetlenül e-n kívül nincs másik érintő.

B.3691.Legfeljebb milyen nagy lehet egy 3x4x12 méretű téglatest merőleges vetületének a területe?

(5 pont)

Megoldás: Ha a téglatestet vetítjük, a vetület olyan síkidom lesz, amelyet a téglatest bizonyos éleinek vetületei határolnak. A T téglatest élei 3 csoportba oszthatók, minden egyes csoportban 4 egymással párhuzamos, egyenlő hosszúságú él szerepel. Ha a vetítés olyan egyenes mentén történik, amely nem párhuzamos a téglatest egyik lapsíkjával sem, akkor a vetület olyan középpontosan szimmetrikus ABCDEF hatszög lesz, melynek határoló élei mindhárom csoportból két-két alkalmas él vetületeként jönnek létre. Ez akkor is igaz lesz, ha a vetítés nem ilyen egyenes mentén történik, csakhogy ebben az esetben a hatszög elfajuló. Tekintsük ugyanis a vetületet, ez egy olyan H sokszög, melynek csúcsai a T bizonyos csúcsainak vetületeként jelentkeznek. Ha például az B csúcs a téglatest B' csúcsának vetülete, akkor a vetület B-ből induló oldalai, vagy legalábbis azok kezdő szakaszai a T valamely A'B' és B'C' élének vetületeként jönnek létre. Legyen az A'B' él a, a B'C' és pedig b hosszúságú, ahol a és b a {3,4,12} halmaz két különböző eleme. Az A',C' pontok A-val, illetve C-vel jelölt vetületei tehát H B-ből induló oldalaira esnek, általános esetben ezen oldalak végpontjai lesznek. Ha a {3,4,12} halmaz harmadik elemét c-vel jelöljük, akkor a téglatest B'-ből induló, c hosszúságú élének vetülete az ABC szögtartományba esik. Jelölje D' a T-nek C'-ből induló c hosszúságú élének másik végpontját, és legyen D a D' pont vetülete. Mivel párhuzamos szakaszok vetülete is egymással párhuzamos, a C'-ből induló a hosszúságú él vetülete, és így az egész T téglatest vetülete is a BCD szögtartományba esik, ahol elfajuló esetben a BCD szög egyenes szög. Az eljárást tovább folytatva kapjuk az ABCDEF hatszöget, melynek egymás utáni oldalai rendre a,b,c,a,b,c hosszú élek vetületeként jöttek létre. E hatszög területe kétszerese az ACE háromszög területének.

Az elmondottak alapján világos, hogy az ACE háromszög egy olyan A'C'E' háromszög vetületeként jött létre, melyet T különböző hosszúságú lapátlói határolnak. Ezen lapátlók hossza a Pithagorasz tétel alapján 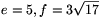$e=5,f=3\sqrt{17}$ , illetve 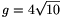$g=4\sqrt{10}$ . Az ACE háromszög területe nem lehet nagyobb az A'C'E' háromszög t területénél, melyet a Héron-képlet alapján kiszámolhatunk:

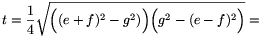
$t={1\over4}\sqrt{\Bigl((e+f)^2-g^2)\Bigr)\Bigl(g^2-(e-f)^2\Bigr)}=$

$={1\over4}\sqrt{(40\sqrt{10}+32)(40\sqrt{10}-32)}= \sqrt{1000-64}=6\sqrt{26}.$

A H vetület területe nem lehet nagyobb, mint 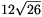$12\sqrt{26}$ , ami el is érhető, ha a téglatestet egy olyan síkra vetítjük, amely párhuzamos T két, közös csúcsból kiinduló lapátlójával.

Már regisztráltál?
Új vendég vagy?