A 2004. szeptemberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3742. Egy 35 fős osztály tanulói két csoportba oszthatók: a kockafejűekre és az égimeszelőkre. Az égimeszelők állítják, hogy magasabbak a kockafejűeknél, akik viszont jobb matekosnak tartják magukat. Egyikük egyszer azt kérdezte egy égimeszelőtől: ,,Mit értetek azon, hogy ti magasabbak vagytok nálunk? Talán azt, hogy

1. Minden égimeszelő magasabb valamennyi kockafejűnél?

2. Több alacsonyabb kockafejű van a legalacsonyabb égimeszelőnél, mint ahány alacsonyabb égimeszelő van a legmagasabb kockafejűnél?

3. Többen vannak azok az égimeszelők, akiknél vannak alacsonyabb kockafejűek, mint azok a kockafejűek, akiknél vannak alacsonyabb égimeszelők?

4. A kockafejűek átlagmagassága kisebb az égimeszelők átlagmagasságánál?''

A kérdések hallatán az égimeszelő szemmel láthatóan összezsugorodott ... A feladat viszont az, hogy megállapítsuk, milyen viszonyban állnak a fenti kijelentések, azaz bármely két állítás esetén döntsük el, következik-e egyikükből a másik.

(4 pont)

(Hugo Steinhaus nyomán)

Megoldás: Először is jegyezzük meg, hogy a szöveg alapján nyilvánvaló, hogy legalább egy kockafejű és legalább egy égimeszelő van az osztályban. Az első állításból nyilván következik a másik három állítás mindegyike. Megmutatjuk, hogy az állítások között semmilyen egyéb implikáció nincs.

Először megmutatjuk, hogy sem a második, sem a harmadik állításból nem következik a negyedik. Legyen ehhez az osztályban tizenkilenc 170 cm magas kockafejű, tizenöt 171 cm magas égimeszelő, és még egy 190 cm magas kockafejű. Ekkor a 2. és 3. állítás igaz, a 4. viszont nem, hiszen a két átlagmagasság éppen ugyanakkora. Ez a példa azt is mutatja, hogy sem a második, sem a harmadik állításból nem következik az első.

Most arra mutatunk példát, amikor a 2. és a 4. állítás érvényes, az 1. és a 3. azonban nem. Ehhez legyen az osztályban tizenöt 170 cm magas kockafejű, tíz 179 cm magas égimeszelő, és ugyanennyi 180 cm magas kockafejű.

Már csak azt kell megmutatnunk, hogy sem a harmadik, sem a negyedik állításból nem következik a második. Erre pedig alkalmas a következő példa: legyen az osztályban tíz 170 cm magas kockafejű, tizenöt 176 cm magas égimeszelő, öt 179 cm magas kockafejű, és még ugyanennyi 180 cm magas égimeszelő.

Ezzel mind a 12 lehetséges esetet áttekintettük.

B.3743. Vágjuk szét az ábrán látható paralelogrammát két részre úgy, hogy a részekből egy egységnyi élű kockát lehessen hajtogatni.

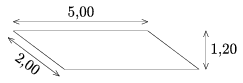
(5 pont)

Javasolta: Hajba Károly (Kisvárda)

Megoldás: Vegyük fel a Descartes-féle koordinátarendszerben az A(0;0), B(2;0), C(6;3) és D(4;3) pontokat. Ekkor az ABCD paralelogrammában AB=CD=2, a Pithagorasz-tétel alapján pedig BC=DA=5. Mivel a négyszög területe 6 egység, a BC és DA oldalak távolsága 6:5=1,20, az ABCD négyszög tehát egybevágó az ábrán látható paralelogrammával. Azt is megtehetjük tehát, hogy a koordinátarendszert igazítjuk az adott paralelogrammához. Tekintsük a P(2;1), Q(3;1), R(3;2) és S(4;2) pontokat. Nem nehéz megmutatni, hogy ezek a négyszög belsejében helyezkednek el, és hogy a BPQRSD törött vonal azt két egybevágó részre bontja fel. Ha most a baloldali részt az x tengellyel párhuzamosan jobbra két egységgel eltoljuk, a két rész a BC szakasz mentén illeszkedve együttesen egy hat darab egységnégyzetből álló összefüggő alakzatot tesz ki, amelyből könnyen látható módon egységkockát hajtogathatunk, ha azt az egységnégyzeteket elválasztó öt szakasz mentén hajtjuk meg.

B.3744. Hány olyan n pozitív egész szám van, amelyre n²+10n négyzetszám?

(3 pont)

Megoldás: Tegyük fel, hogy n²+10n=a² és n+5=b, ahol a,b pozitív egészek. Ekkor 25=b²-a²=(b+a)(b-a). Mivel b>a, ez csak b+a=25, b-a=1 esetén lehetséges, vagyis ha b=13, n=8. Ekkor viszont n²+10n=144 valóban négyzetszám. A feltételnek tehát pontosan egy n pozitív egész szám tesz eleget.

B.3745. Az a, b, c, d számokra teljesül, hogy a+b>|c-d| és c+d>|a-b|. Bizonyítsuk be, hogy ekkor a+c>|b-d|.

(3 pont)

Megoldás: Az első feltétel szerint a+b>d-c, vagyis a+c>d-b. A második feltétel alapján pedig c+d>b-a, ahonnan a+c>b-d adódik. E két egyenlőtlenség egybevetésével kapjuk a bizonyítandó állítást.

B.3746. Az egyenlő oldalú ABC háromszög AB oldalán adottak az M és N pontok, a BC oldalon a P, a CA oldalon pedig a Q pont úgy, hogy

MA+AQ=NB+BP=AB.

Mekkora szöget zárhatnak be az MP és az NQ egyenesek?

(4 pont)

Megoldás: Mivel AB=BC=CA, a feltétel szerint BN=CP és CQ=AM. A háromszög középpontja körüli megfelelő irányban történő 60^o-os elforgatás a B pontot a C-be, a C pontot az A-ba, az A pontot pedig a B-be viszi. Az AB oldal tehát a BC oldalba, a BC oldal a CA oldalba, ez utóbbi pedig az AB oldalba kerül. Mivel az N,P,Q,M pontok ezeken az oldalakon helyezkednek el, a BN=CP feltétel alapján láthatjuk, hogy az elforgatás során az N pont a P-be kerül. Ugyanilyen alapon a Q pont képe az M pont lesz. Az elforgatás ezek szerint az NBCQ négyszöget a PCAM négyszögbe viszi át, miközben az első négyszög QN oldala a második négyszög MP oldalába kerül. Az MP és NQ egyenesek ennek megfelelően 60^o-os szöget zárnak be egymással.

B.3747. Egy háromszög oldalai a, b, c, területe \(\displaystyle \frac{(a+b+c)(a+b-c)}{4}\). Mekkora a háromszög legnagyobb szöge?

(4 pont)

Megoldás: A Héron-képlet szerint a hármszög területe

\(\displaystyle {1\over4}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}.\)

Ezt a feltétellel összevetve, beszorzás, négyzetreemelés és az (a+b+c)(a+b-c) kifejezéssel való leosztás után az

(a+c-b)(b+c-a)=(a+b+c)(a+b-c),

vagyis a c²-(a-b)²=(a+b)²-c² összefüggéshez jutunk. Ezt átalakítva

2c²=(a+b)²+(a-b)²=2(a²+b²)

adódik. A Pithagorasz-tétel megfordítása szerint a háromszög c oldallal szemben lévő szöge derékszög, ami tehát egyben a háromszög legnagyobb szöge is.

B.3748. Az ABC háromszög C csúcsából induló magasságvonal és súlyvonal harmadolják a BCA szöget. Igazoljuk, hogy a háromszög derékszögű.

(4 pont)

Megoldás: Legyen az AB oldal felezőpontja F, és tegyük fel, hogy a C csúcsból induló magasságvonal M talppontja az AF szakaszra esik. Mivel az ACM és FCM szögek nagysága megegyezik, az ACM és FCM derékszögű háromszögek egybevágók. Ezért AM=MF, vagyis az MF szakasz hossza fele az FB szakasz hosszának. Az MCB háromszög C-nél lévő szögét felezi a CF félegyenes. A szögfelező-tétel szerint tehát CM:CB=MF:BF=1:2. A BCM szög ennélfogva 60^o-os, a BCA szög pedig derékszög.

B.3749. Egy téglalap oldalai 5 cm és 9 cm hosszúak. A téglalapot feldaraboljuk tíz olyan téglalapra, amelyek oldalhosszai cm-ben kifejezve egész számok. Bizonyítsuk be, hogy a darabok között van két egybevágó.

(5 pont)

Megoldás: Vizsgáljuk meg, hogy hány adott t területű, egész oldalhosszúságú téglalap létezik egyáltalán, ha az egymással egybevágóakat nem különböztetjük meg. Legyen ez a szám A(t). Nyilván A(t)=1 ha t=1, vagy ha t prímszám, ha pedig t két (nem feltétlenül különböző) prímszám szorzata, akkor A(t)=2. Ezek szerint

A(1)=A(2)=A(3)=1, A(4)=2, A(5)=1, A(6)=2, A(7)=1, A(8)=2.

Ha egy T téglalapot fel lehet darabolni tíz olyan téglalapra, melyek oldalai cm-ben kifejezve egész számok és nincs közöttük két egybevágó, akkor T területe négyzetcentiméterekben kifejezve legalább akkora, mint a 10 legkisebb különböző, egészoldalhosszúságú téglalap területének összege, ami

1+2+3+2^.4+5+2^.6+7+8=46.

Egy 45 négyzetcentiméter területű téglalapot tehát nem lehet ilyen módon feldarabolni, ami bizonyítja az állítást.

B.3750. Az {a_n} sorozatról tudjuk, hogy a₁ < a₂ pozitív egész szám, továbbá k\(\displaystyle \ge\)3 esetén a_k = 4a_k-1-3a_k-2. Igazoljuk, hogy a₄₅ > 3⁴³.

(4 pont)

Megoldás: Legyen k\(\displaystyle \ge\)1 esetén b_k=a_k+1-a_k, ekkor b₁ pozitív egész szám, és minden k\(\displaystyle \ge\)1 esetén b_k+1=3b_k is pozitív egész. Következésképpen az a_k sorozat szigorúan növekedő, és a₄₅>b₄₄=3⁴³b₁\(\displaystyle \ge\)3⁴³, amint azt bizonyítani kellett.

B.3751. Legyen \(\displaystyle f(x)=\frac{x}{1-x}\). Határozzuk meg a valós számok halmazának azt a legbővebb részhalmazát, ahol minden pozitív egész n esetén az

\(\displaystyle f^{(n)}(x)=\underbrace{f\big(f\big(\dots\big(f}_{n}(x)\big)\dots\big)\big) \)

összetett függvény értelmezhető.

(4 pont)

Megoldás: Jelölje S(n) a keresett halmaz komplementerét. Nyilván \(\displaystyle S(1)\subseteq S(2)\subseteq S(3)\subseteq\ldots\), és S(1)={ 1}. Ha \(\displaystyle x\not\in S(1)\), akkor

\(\displaystyle f^{(2)}(x)=f(f(x))=f({x\over1-x})= {{x\over1-x}\over{1-{x\over1-x}}}={x\over1-2x},\)

feltéve, hogy ez utóbbi kifejezés értelmezhető. Az x\(\displaystyle \ne\)1 feltétel miatt ugyanis a számlálót és a nevezőt egyaránt bővíthetjük az 1-x kifejezéssel. Ezért S(2)={ 1, 1/2}. Hasonlóképpen láthatjuk, hogy \(\displaystyle x\not\in S(2)\) esetén \(\displaystyle f^{(3)}(x)={x\over1-3x}\), feltéve hogy ez a kifejezés értelmes, vagyis ha x\(\displaystyle \ne\)1/3, az f⁽³⁾(1/3) kifejezés pedig nem értelmazhető. Ezután nem nehéz n szerinti teljes indukcióval igazolni, hogy S(n)={ 1,1/2,1/3,...,1/n} teljesül minden n pozitív egész számra, továbbá hogy \(\displaystyle x\not\in S(n)\) esetén \(\displaystyle f^{(n)}(x)={x\over1-nx}\). Valóban, n=1 esetén ezt már láttuk, ha pedig valamely n pozitív egész számra az állítást már igazoltuk, és \(\displaystyle x\not\in S(n)\), ami az f⁽ⁿ⁺¹⁾ függvény értelmezhetőségének nyilvánvaló feltétele, akkor

\(\displaystyle f^{(n+1)}(x)=f(f^{(n)}(x))=f({x\over1-nx})= {{x\over1-nx}\over{1-{x\over1-nx}}}={x\over1-(n+1)x},\)

feltéve, hogy ez utóbbi kifejezés értelmezhető, vagyis ha x\(\displaystyle \ne\)1/(n+1), az f⁽ⁿ⁺¹⁾(1/(n+1)) kifejezés pedig nem értelmezhető. Ezzel az indukciós lépést igazoltuk, a feladatban keresett halmaz pedig az S(n)={ 1,1/2,1/3,...,1/n} halmaz komplementere.