A 2004. októberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3752. Mutassuk meg, hogy ha egy konvex nyolcszög szemközti oldalai párhuzamosak és egyenlők, akkor a sokszög feldarabolható paralelogrammákra.

(3 pont)

Megoldás: Legyenek a nyolcszög csúcsai valamilyen körüljárás szerint sorban A,B,C,D,E, F,G,H. Az ABEF négyszög paralelogramma, tehát az FAB és EBA szögek összege éppen 180^o. A konvexitás miatt a HAB és CAB szögek összege nagyobb lesz, mint 180^o, és ugyanez elmondható a nyolcszög két tetszőleges egymás utáni szögéről.

Legyen A' az a pont, amelyre a HABA' négyszög paralelogramma, ekkor az A' pont az ABEFGH hatszög belső pontja lesz, vagyis a HABA' paralelogramma az a nyolcszög része. Ugyanígy ha D' jelöli azt a pontot, amelyre a CDED' négyszög paralelogramma, úgy a D' pont szintén a nyolcszög belső pontja lesz. Mivel az AH és DE vektorok egyenlők, ugyanez igaz a BA' és CD' vektorokra is, a BCD'A' négyszög tehát olyan paralelogramma, amely a nyolcszögnek része. Továbbá \(\displaystyle \overrightarrow{FE}=\overrightarrow{AB}=\overrightarrow{HA'}\), \(\displaystyle \overrightarrow{HG}=\overrightarrow{CD}=\overrightarrow{D'E}\) és \(\displaystyle \overrightarrow{GF}=\overrightarrow{BC}=\overrightarrow{A'D'}\). Vagyis a nyolcszöget felbontottuk az ABA'H, BCD'A', CDED' paralelogrammákra és a HA'D'EFG konvex hatszögre, melyben a szemközti oldalak ismétcsak párhuzamosak és egyenlők. Már csak a hatszöget kell felbontanunk paralelogrammákra. Ennek része a HGED' paralelogramma, ezért ha F' jelöli azt a pontot amelyre az EFGF' négyszög paralelogramma, ez a pont a HD'EFG ötszög belsejében lesz. Továbbá a GHA'F' és ED'A'F' négyszögek is paralelogrammák lesznek, igazolván a keresett felbontás létezését.

B.3753. Jelölje S_m az (a_m) sorozat első m elemének az összegét. Bizonyítsuk be, hogy ha minden n\(\displaystyle \ne\)k pozitív egészre teljesül, hogy

\(\displaystyle \frac{S_{n+k}}{n+k}=\frac{S_n-S_k}{n-k}, \)

akkor (a_m) számtani sorozat.

(3 pont)

Megoldás: A feltételt n=2, k=1 esetén alkalmazva kapjuk, hogy

\(\displaystyle {a_1+a_2+a_3\over3}={a_2},\)

ahonnan a₁+a₃=2a₂, a₃-a₂=a₂-a₁ következik. Az a₁=a, a₂-a₁=d jelöléssel tehát a₂=a+d és a₃=a+2d. Tegyük fel hogy valamely n\(\displaystyle \ge\)3 egész számra már bebizonyítottuk, hogy minden 1\(\displaystyle \le\)i\(\displaystyle \le\)n esetén a_i=a+(i-1)d. Ekkor a feltételt ismétcsak k=1 esetén felhasználva

\(\displaystyle {a_1+a_2+\ldots+a_{n+1}\over n+1}={a_2+\ldots+a_n\over n-1}\)

adódik, ahonnan átrendezés után

(n-1)a_n+1=2(a₂+...+a_n)-(n-1)a₁=

=2S_n-(n+1)a=n(2a+(n-1)d)-(n+1)a=(n-1)(a+nd),

vagyis a_n+1=a+nd. Innen az állítás azonnal következik a teljes indukció elve alapján.

B.3754. Bizonyítsuk be, hogy a szabályos háromszög nem bontható föl öt egybevágó háromszögre.

(5 pont)

Megoldás: Tegyük fel, hogy létezik egy ilyen felbontás. A felbontásban szereplő öt háromszög szögeinek összege 5\(\displaystyle \pi\). Először is, a szabályos háromszög minden egyes oldalán kell legyen legalább egy osztópont, ugyanis ellenkező esetben valamelyik kis háromszög egyik oldala ugyanolyan hosszú lenne, mint az eredeti háromszög oldala. Mivel a szabályos háromszögben csak két csúcs helyezkedhet el egymástól ilyen nagy távolságra, és minden egyes kis háromszögnek kell, hogy legyen ilyen hosszú oldala, a felbontásban legfeljebb három kis háromszög szerepelhetne.

Tekintsük a felbontásban szereplő háromszögeknek az eredeti háromszög csúcsainál, valamint az oldalakon lévő három osztópontnál lévő szögeit: ezek összege 4\(\displaystyle \pi\). Két esetet különböztethetünk meg ennek következtében. Vagy az eredeti háromszög valamelyik oldalán van még egy osztópont, más osztópont pedig nincs, vagy pedig a háromszög belsejében talalható még egy osztópont, amely valamelyik kis háromszög egy oldalának belső pontja is egyben.

A kis háromszögeknek összesen 15 szöge van. Tegyük fel először, hogy minden osztópont körül legalább három ilyen szög helyezkedik el. Ez csak úgy lehetséges, ha mindenhol pontosan három szög helyezkedik el, a fennmaradó három szög pedig az eredeti háromszög egy-egy csúcsához illeszkedik. Ha most a háromszög oldalain lévő osztópontok és a háromszög A,B,C csúcsai a háromszög kerületén A,X,B,Y,Z,C,U sorrendben helyezkednek el, akkor az AXU, BXY, CUZ háromszögeknek szerepelnie kell a felbontásban, a fennmaradó két háromszög pedig az XYZU négyszöget osztja két részre. Ekkor azonban vagy az Y, vagy a Z osztópont körül csak két szöge helyezkedik el a kis háromszögeknek, ami ellentmondás. A másik esetben, ha a csúcsok és az X,Y,X osztópontok A,X,B,Y,C, X sorrendben helyezkednek el, az AXZ, BYX, CZY háromszögeknek kell szerepelni a felbontásban, a fennmaradó két kis háromszög pedig az XYZ háromszöget osztaná két részre, ami ugyancsak ellentmondásra vezetne.

Már csak azt az esetet kell megvizsgálni, ha valamelyik osztópont körül a kis háromszögeknek csak két szöge helyezkedik el. Ez nem lehet a kis háromszög két különböző nagyságú szöge, a kis háromszög tehát ekkor mindenképpen derékszögű. Ha most az A,B,C csúcsok valamelyike körül két szög is található, akkor ezek szükségképpen egyenlők, ellenkező esetben a kis háromszögnek lenne két különböző szöge, melyek összege kisebb lenne \(\displaystyle \pi\)/2-nél. Egy ilyen szög tehát legfeljebb \(\displaystyle \pi\)/6 nagyságú, a kis háromszög harmadik szöge tehát legalább \(\displaystyle \pi\)/3. Mivel az öt kis háromszögnek együttesen öt legfeljebb \(\displaystyle \pi\)/6 nagyságú szöge van, nem lehet az A,B,C csúcsok mindegyike körül legalább kettő közülük. Ebből azonnal következik, hogy a kis háromszög szögei \(\displaystyle \pi\)/6, \(\displaystyle \pi\)/3 és \(\displaystyle \pi\)/2.

Feltehetjük tehát, hogy a kis háromszög oldalainak hossza \(\displaystyle 1,\sqrt{3}\) és 2. Ekkor a szabályos háromszög aldalának d hosszúságára csak a 2, \(\displaystyle 1+\sqrt{3}\), 3, \(\displaystyle 2\sqrt{3}\), \(\displaystyle 2+\sqrt{3}\) és a 4 értékek jöhetnének szóba. Mivel az öt kis háromszög együttes területe megegyezik a nagy háromszögével, szükségképpen \(\displaystyle \sqrt{3}d^2/4=5\cdot(\sqrt{3}/2)\). Mivel azonban d²=10 a fenti értékek egyikére sem teljesül, ebben az esetben is ellentmondásra jutunk, ami az állítást igazolja.

B.3755. Egy kör úgy metszi egy konvex négyszög oldalait egy-egy szakaszban, hogy a négyszög belsejébe eső szemközti körívek hosszának összege egyenlő. Bizonyítsuk be, hogy a négyszög húrnégyszög.

(4 pont)

Megoldás: Legyen a kör középpontja O, a négyszög csúcsai pedig rendre A,B,C,D. Jelölje a körnek az AB oldallal alkotott metszéspontjait A' és B'' úgy, hogy az A csúcshoz az A' pont van közelebb. Definiáljuk hasonló módon a B', C'', C', D'', D' és A'' pontokat is. Az A'OB'', B'OC'', C'OD'' és D'OA'' egyenlő szárú háromszögek alapján fekvő szögek nagysága legyen rendre \(\displaystyle \alpha\)', \(\displaystyle \beta\)', \(\displaystyle \gamma\)' és \(\displaystyle \delta\)'. Legyen továbbá az A'OA'', B'OB'', C'OC'', D'OD'' szögek nagysága rendre \(\displaystyle \alpha\)'', \(\displaystyle \beta\)'', \(\displaystyle \gamma\)'' és \(\displaystyle \delta\)''; ekkor a feltétel szerint \(\displaystyle \alpha\)''+\(\displaystyle \gamma\)''=\(\displaystyle \beta\)''+\(\displaystyle \delta\)''.

Az AA'OA'' négyszögben az AA'O és AA''O szögek nagysága rendre \(\displaystyle \pi\)-\(\displaystyle \alpha\)' és \(\displaystyle \pi\)-\(\displaystyle \delta\)', ahonnan a négyszög A csúcsánál lévő \(\displaystyle \alpha\) szög nagyságára

\(\displaystyle \alpha\)=2\(\displaystyle \pi\)-(\(\displaystyle \pi\)-\(\displaystyle \alpha\)')-\(\displaystyle \alpha\)''-(\(\displaystyle \pi\)-\(\displaystyle \delta\)')=\(\displaystyle \alpha\)'+\(\displaystyle \delta\)'-\(\displaystyle \alpha\)''

adódik. Ugyanígy a négyszög B,C,D csúcsainál lévő szögeinek nagysága rendre \(\displaystyle \beta\)=\(\displaystyle \beta\)'+\(\displaystyle \alpha\)'-\(\displaystyle \beta\)'', \(\displaystyle \gamma\)=\(\displaystyle \gamma\)'+\(\displaystyle \beta\)'-\(\displaystyle \gamma\)'' és \(\displaystyle \delta\)=\(\displaystyle \delta\)'+\(\displaystyle \gamma\)'-\(\displaystyle \delta\)''. Látható, hogy \(\displaystyle \alpha\)+\(\displaystyle \gamma\)=\(\displaystyle \beta\)+\(\displaystyle \delta\), vagyis a négyszög valóban húrnégyszög.

B.3756. A nyolcjegyű számokat osszuk két halmazba. Az egyik halmazba kerüljenek azok, amelyek felbonthatók két négyjegyű szám szorzatára, a másikba azok, amelyek nem. Melyik halmazba kerül több szám?

(5 pont)

Megoldás: Összesen N=9000 négyjegyű szám van, a nyolcjegyűek száma pedig 9^.10⁷. Ha F-fel jelöljük azon nyolcjegyű számok számát melyek felbonthatók két négyjegyű szám szorzatára (esetleg többféle módon is), akkor \(\displaystyle F\le N+{N\choose2}\), hiszen minden szóban forgó szám vagy két egyeforma, vagy két különböző négyjegyű szám szorzata lesz. Ennélfogva

\(\displaystyle F\le N+{N\choose2}={N(N+1)\over2}<{9000\cdot10000\over2}= {9\cdot10^7\over2}.\)

Vagyis azon nyolcjegyű számok száma, melyek felírhatók két négyjegyű szám szorzataként, kisebb az összes nyolcjegyű szám számának felénél, tehát a második halmazba kerül több szám.

B.3757. A k₁ és a k₂ körök az A és a B pontokban metszik egymást, egyik közös érintőjük pedig az E₁, illetve az E₂ pontokban érinti a köröket. Bizonyítsuk be, hogy az A, E₁, E₂, illetve a B, E₁, E₂ pontokon átmenő körök sugara egyenlő.

(4 pont)

Megoldás: Tegyük fel, hogy E₁, E₂ a két kör közös szimmetriatengelyének ugyanazon az oldalán van, mint az A pont. Jelölje az AE₁E₂ és BE₁E₂ háromszögek köré írt körök sugarát rendre R_A és R_B. Az ABE₁ és AE₁E₂ szögek nagysága megegyezik, legyen ez \(\displaystyle \alpha\). Hasonlóképpen legyen az egymással egyenlő ABE₂ és AE₂E₁ szögek nagysága \(\displaystyle \beta\). A BE₁E₂ háromszögre a szinusz-tételt felírva E₁E₂=2R_Bsin (\(\displaystyle \alpha\)+\(\displaystyle \beta\)). Hasonlóképpen kapjuk az AE₁E₂ háromszögből, hogy E₁E₂=2R_Asin (\(\displaystyle \pi\)-\(\displaystyle \alpha\)-\(\displaystyle \beta\)). Lévén sin x=sin (\(\displaystyle \pi\)-x), a két sugár egyenlősége innen azonnal leolvasható.

B.3758. Legyen az n pozitív páros szám. Írjuk az 1,2,...,n² számokat egy nxn-es táblázat mezőibe úgy, hogy a táblázat k-adik sorában az elemek balról jobbra olvasva rendre (k-1)n + 1, (k-1)n + 2, ..., (k-1)n + n legyenek (k = 1,2,...,n).

Színezzük ki az így kitöltött táblázat mezőit bordó és sárga színnel úgy, hogy minden sorban és minden oszlopban a mezők fele bordó, a másik fele pedig sárga legyen. (A sakktábla-szerű színezés például egy lehetőség.) Bizonyítsuk be, hogy minden ilyen színezésre a bordó és a sárga mezőkön lévő számok összege egyenlő.

(4 pont)

Megoldás: Egy négy mezőből álló elrendezést nevezzünk téglalapnak, ha két sor és két oszlop metszeteként jön létre, és pontosan két sárga és két bordó mezőből áll olyan módon, hogy az azonos színű mezők a téglalap átellenes csúcsainál helyezkednek el. Könnyű kiszámolni, hogy egy ilyen téglalapban a sárga mezőkre írt számok összege megegyezik a bordó mezőkre írt számok összegével. Mivel a sakktábla-szerű színezés nyilvánvaló módon téglalapokra particionálható, ilyen színezés esetén az állítás igaz. Az is nyilvánvaló, hogy ha a színezést úgy változtatunk meg, hogy egy téglalap mezőinek színét ellenkezőjére cseréljük, az így kapott színezésben (mely ugyancsak megfelelő színezés lesz) a bordó mezőkön található számok összege ugyanaz lesz, mint a változatatás előtt, és ugyanez áll a sárga mezőkön található számok összegére. A színezés ilyen módon történő megváltoztatását nevezzük cserének.

Elelegendő tehát azt megmutatni, hogy tetszőleges színezésből egymást követő cserék alkalmas véges sorozatával sakktábla-szerű színezést tudunk előállítani. Tegyük fel, hogy az 1,2,..., N-1 számokat tartalmazó mezők színezése megfelel a sakktábla-szabálynak, de az N-edik mező színe már nem. Nyilván N>1. Tegyük fel, hogy ez a mező éppen az i-edik sor j-edik eleme. Mivel minden sorban, és minden oszlopban ugyanannyi sárga, illetve bordó mező van, nyilván i<n és j<n. Az egyszerűség kedvéért legyen ennek a mezőnek a színe bordó. Ekkor valamilyen \(\displaystyle \ell\)>j esetén az i-edik sor \(\displaystyle \ell\)-edik eleme sárga, ellenkező esetben ugyanis az i-edik sorban több bordó mező lenne, mint sárga. Tekintsük most a j-edik oszlopot, ebben az oszlopban az első i-1 mező közül \(\displaystyle \lceil{i-1\over2}\rceil\) számú mező színe bordó, \(\displaystyle \lfloor{i-1\over2}\rfloor\) számú mező színe pedig sárga. Az \(\displaystyle \ell\)-edik oszlopban az említett bordó mezőkkel megegyező sorban (a sakktábla- színezés miatt) minden mező sárga, éppúgy, mint az i-edik sorban lévő mező. Ezért, ha minden egyes k>i esetén igaz lenne, hogy valahányszor a j-edik oszlop k-adik eleme sárga, akkor az \(\displaystyle \ell\)-edik oszlop k-adik eleme is sárga, azt kapnánk, hogy az \(\displaystyle \ell\)-edik oszlopban legalább

\(\displaystyle \Big\lceil{i-1\over2}\Big\rceil+1+\Bigl(n-\Big\lfloor{i-1\over2}\Big\rfloor\Bigr\)n">

sárga mező lenne, ami lehetetlen.

Ezért találhatunk olyan téglalapot, melynek bal felső sarka éppen az i-edik sor j-edik eleme. Ezen a téglalapon egy cserét végrehajtva ismét jó színezést kapunk, de most már az első N számot tartalmazó összes mező színezése megfelel a sakktábla szabálynak, hiszen a változtatás az első N-1 számot nem érintette. Ezt ismételgetve, véges sok cserével elérthetjük, hogy az egész táblázat sakktábla-szerűen legyen kiszínezve.

B.3759. Bizonyítsuk be, hogy minden k pozitív egész számra (2k)! osztható k!^.(k+1)!-sal.

(4 pont)

Megoldás: Mivel \(\displaystyle {2k+1\choose k}={(2k+1)!\over k!(k+1)!}\), az m=(k!)² jelöléssel kapjuk, hogy m(k+1) osztója a (2k+1)(2k)! számnak. Az is igaz, hogy (2k)! osztható m-mel, hiszen \(\displaystyle {2k\choose k}={(2k)!\over m}\) szintén egész szám. Innen kapjuk, hogy \(\displaystyle (2k+1){2k\choose k}\) osztható k+1-gyel. Mivel 2k+1=2(k+1)-1, látható, hogy 2k+1 és k+1 relatív prímek, vagyis \(\displaystyle 2k\choose k\) is osztható k+1-gyel. Következésképpen (2k)! osztható m(k+1)-gyel, vagyis k!(k+1)!-sal.

B.3760. Az ábrán látható téglatestben az EH él felezőpontja S, a HG él felezőpontja R és a GF él felezőpontja Q. Bizonyítsuk be, hogy az ASR és a DRQ háromszögek területe egyenlő.

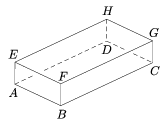
(4 pont)

Megoldás: Jelölje X and RS és EF egyenesek metszépontját, Y pedig a QR és EH egyenesek metszéspontját. Ekkor az XES, RHS, RHY és RCQ háromszögek egybevágó derékszögű háromszögek, ahonnan XS=RS=RY=RQ adódik. Következésképpen az AS szakasz az XAS háromszög súlyvonala, míg a DR szakasz az YDQ háromszög súlyvonala. Elég tehát megmutatni, hogy az XAS és RDY háromszögek területe egyenlő. Ez a két háromszög azonban egybevágó, hiszen mint már láttuk, XS=RY, továbbá AS=DY és AX=DR. Itt az AS=DY egyenlőség az AES és DHY derékszögű háromszögek egybevágóságából következik, AX=DR pedig arra vezethető vissza, hogy az AEX és DHR derékszögű háromszögek egyebevágók.

B.3761. Oldjuk meg az alábbi egyenletrendszert:

\(\displaystyle \frac{1}{x}+\frac{1}{2y}=(x^2+3y^2)(3x^2+y^2),\)

\(\displaystyle \frac{1}{x}-\frac{1}{2y}=2(y^4-x^4).\)

(5 pont)

Megoldás: Az egyenletrendszerben szereplő kifejezések pontosan akkor értelmesek, ha sem x sem y nem 0. A két egyenlet összeadásával illetve kivonásával az eredetivel ekvivalens

\(\displaystyle {2\over x}=x^4+5y^4+10x^2y^2,\quad{1\over y}=5x^4+y^4+10x^2y^2\)

egyenletrenszerhez jutunk. Az x\(\displaystyle \ne\)0, y\(\displaystyle \ne\)0 feltételek mellett ez ekvivalens az

x⁵+10x³y²+5xy⁴=2, 5x⁴y+10x²y³+y⁵=1

egyenletrendszerrel. Összeadás és kivonás után az ezzel továbbra is ekvivalens

(x+y)⁵=3, (x-y)⁵=1

egyenletrendszerhez jutunk, melynek megoldása

\(\displaystyle x={\root{5}\of3+1\over2},\quad y={\root{5}\of3-1\over2}.\)

Mivel ezen számok egyike sem 0, az eredeti egyenletrendszernek is ez az egyetlen megoldása.