A 2004. novemberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 780. Egy matematika versenyen három feladatot tűztek ki. Az első feladatot a résztvevők 85 százaléka oldotta meg, a másodikat 80, a harmadikat pedig 75 százalékuk. Bizonyítsuk be, hogy legalább 40 százalékuk megoldotta mind a három feladatot.

Megoldás. Az első feladatot legfeljebb a résztvevők 15 százaléka nem oldotta meg, a másodikat legfeljebb 20, a harmadikat legfeljebb 25 százalékuk. Így, a legrosszabb esetben a versenyzőknek legfeljebb a 15 + 20 + 25 = 60 százaléka nem boldogult legalább egy feladattal, tehát 40 százalékuk valamennyi feladatot megoldotta.

C. 781. Határozzuk meg azokat a pozitív p>q>r prímszámokat, amelyekre

p²- (q+r)²=136.

Megoldás. (p+q+r)(p-q-r)= 136 = 17 ^.8, p+q+r és a nála kisebb p-q-r paritása megegyezik, és mindketten pozitívak. Így p+q+r = 68 és p-q-r = 2, vagy p+q+r = 34 és p-q-r = 4. Mindkét esetben a három prím összege páros, ezért a legkisebbik r=2. A p+q és p-q ismeretében p és q értéke mindkét esetben meghatározható, az egyetlen megoldás p=19, q=13, r=2.

C. 782. A parttal párhuzamosan, attól 200 méterre halad egy vitorlás a Balatonon. Valaki folyamatosan egy irányban úszva szeretné elérni a közeledő hajót. A parthoz képest milyen szögben kell elindulnia, ha a vitorlás sebessége 15 km/h, az úszó sebessége 2 km/h, és induláskor a parton mérve 2 km távolságban van a hajótól?

Javasolta: Koncz Levente (Budapest)

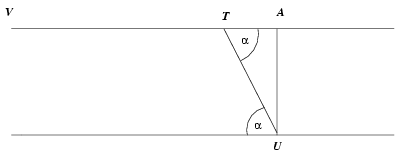
Megoldás. Jelölje a vitorlás helyét kezdetben V, az úszó helyét U, a találkozás helyét T. Legyen továbbá AU = 200. Találkozásukig a vitorlás $\displaystyle VT=VA-TA =2000-200\text{ctg\,}\alpha$, az úszó pedig $\displaystyle UT= \dfrac{200}{\sin\alpha}$ métert tesz meg. A megtett utak aránya sebességük arányával egyenlő, ezért

$\displaystyle 2000-200\text{ctg\,}\alpha=\dfrac{15}{2}\cdot\dfrac{200}{\sin\alpha},$

rendezve

$\displaystyle 10\sin\alpha-\cos\alpha=\dfrac{15}{2},\text{\ ill.}$

$\displaystyle \dfrac{10}{\sqrt{101}}\sin\alpha-\dfrac{1}{\sqrt{101}}\cos\alpha= \dfrac{15}{2\sqrt{101}}.$

Jelölje $\displaystyle \beta$ azt a (hegyes)szöget, amelyre $\displaystyle \cos\beta= \dfrac{10}{\sqrt{101}}$, $\displaystyle \sin\beta=\dfrac{1}{\sqrt{101}}$, ekkor $\displaystyle \sin(\alpha-\beta)=\dfrac{15}{2\sqrt{101}}\approx0.7462$, tehát $\displaystyle \alpha$₁ - $\displaystyle \beta$48.26^o, ill. ₂ - 131.73^o. Mivel 5.71^o, ₁ 53.97^o, ₂ 137.44^o. Ha a feladat szövegét kiegészítjük azzal az életszerű feltétellel, hogy az úszó a lehető legrövidebb utat kívánja megtenni, akkor az egyetlen megoldás ₁53.97^o.

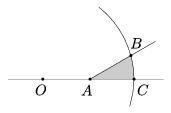
C. 783. Az ábrán látható szürkével jelölt tartományt az A csúcsú 30^o-os szög szárai és egy O középpontú körív határolják. Mekkora a tartomány területe, ha

AO=AB=1.

Megoldás. Az OAB szög 150^o-os, mivel a 30^o-os BAC kiegészítő szöge. Az egyenlőszárú OAB háromszög másik két szöge ezért 15^o. Ebből OC = OB = 2cos 15^o, így a BOC körcikk területe ,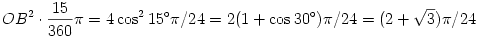

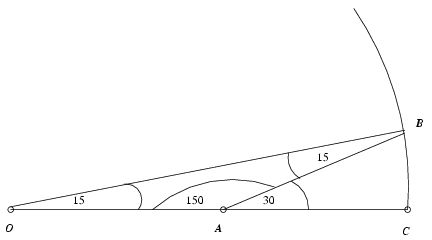
az OAC háromszög területe pedig 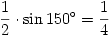. Az ACB tartomány területe tehát e kettő különbsége, .

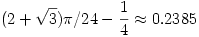C. 784. Az ABCDEFGH téglatestben - a szokásos betűzéssel - AE = 1, AD = 2, AB=3. Mekkora annak a testnek a térfogata, amelynek a csúcsai A és C, valamint az EFGH lap éleinek a felezőpontjai?

Megoldás.

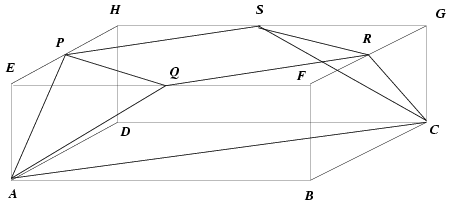
A kapott test a téglatestből úgy kapható, hogy abból kivágjuk az ABCQFR és a vele egybevágó ACDPSH csonkagúlát valamint az EAQP és a vele egybevágó GSRC tetraédert. Előbbiek térfogata 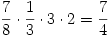, utóbbiaké 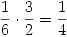, így a test térfogata .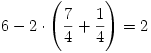