Problem B. 4621. (March 2014)

B. 4621. For a certain tetrahedron, there exists a sphere that touches all edges, and there exists another sphere that touches the three edges bounding one face and also the extensions of the other three edges. Show that there exists a sphere for each face that touches the three edges bounding that face and also the extensions of the other three edges.

(6 pont)

Deadline expired on April 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyenek az érintési pontok \(\displaystyle E\), \(\displaystyle F\), \(\displaystyle G\), \(\displaystyle H\), \(\displaystyle I\), \(\displaystyle J\) az ábra szerint. Mivel egy adott pontból egy adott gömbhöz húzott érintőszakaszok egyenlő hosszúságúak, ezért \(\displaystyle AG=AF=AE=x\), \(\displaystyle BE=BH=BI=y\), \(\displaystyle CH=CJ=CF=z\) és \(\displaystyle DG=DI=DJ=v\).

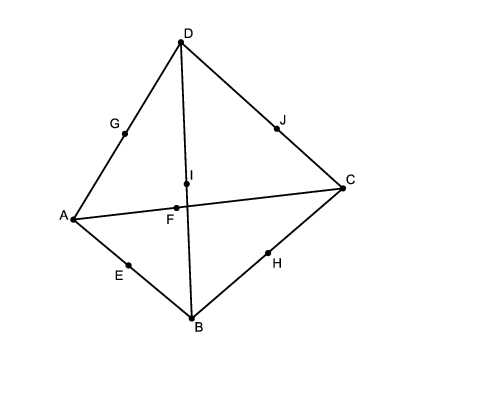
Az élérintő gömb és egy lap síkjának metszete a lap (mint háromszög) beírt köre. Emiatt az egyes lapokon levő érintési pontok az adott lap beírt körének érintési pontjai is.

Legyen az \(\displaystyle ABC\) lap az, amelyhez létezik a megfelelő gömb. Ennek a gömbnek és az \(\displaystyle ABC\) háromszög síkjának metszete szintén az \(\displaystyle ABC\) háromszög beírt köre, így az érintési pontok itt is \(\displaystyle E\), \(\displaystyle H\) és \(\displaystyle F\).

Jelölje az \(\displaystyle AD\), \(\displaystyle BD\), illetve \(\displaystyle CD\) oldalak meghosszabításain levő érintési pontokat rendre \(\displaystyle P\), \(\displaystyle Q\), illetve \(\displaystyle R\). Mivel adott pontból egy adott gömbhöz húzott érintőszakaszok egyenlő hosszúságúak, ezért \(\displaystyle AF=AE=AP=x\), \(\displaystyle BE=BH=BQ=y\) és \(\displaystyle CH=CF=CR=z\). Ugyanezen okból \(\displaystyle DP=DQ=DR\), azaz \(\displaystyle v+2x=v+2y=v+2z\). Ebből \(\displaystyle x=y=z\), tehát az \(\displaystyle ABC\) háromszög szabályos. Mindebből az is következik, hogy a tetraéder minden oldaléle \(\displaystyle x+v\) hosszúságú.

Azt kaptuk, hogy ha egy laphoz létezik a megfelelő gömb, akkor az a lap szabályos.

Ha viszont tekintünk egy olyan nem szabályos tetraédert, amelynek alaplapja szabályos háromszög, a többi lapja pedig egyenlő szárú háromszög, akkor annak csak az alapjához létezhet megfelelő gömb.

Tehát a feladat állítása hamis.

Statistics:

12 students sent a solution.
6 points:	Ágoston Péter, Baran Zsuzsanna, Cseh Kristóf, Csépai András, Di Giovanni Márk, Fekete Panna, Forrás Bence, Lajkó Kálmán, Maga Balázs, Simkó Irén, Williams Kada.
1 point:	1 student.

Problems in Mathematics of KöMaL, March 2014