KöMaL Problems in Physics, December 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on January 11, 2010. |
M. 301. If a flat pocket of vanilla-sugar or other (for example filled with backing powder) pocket is thrown onto a horizontal tabletop, then the pocket does not bounce back, instead, after the collision it begins to slide, and then it stops. Measure how the braking distance depends on the speed of the pocket right before the impact, and on the angle (measured from the horizontal) at which it hits the table.
(6 pont)
 |
Problems with sign 'P'Deadline expired on January 11, 2010. |
P. 4204. What is the colour of the sky in the daytime on the Moon? Observed from the Moon what is the colour of the Earth and of the Mars?
(3 pont)
solution (in Hungarian), statistics
P. 4205. In a straight glass tube, closed at one end, a certain amount of air is enclosed by a mercury line. The glass tube is inclined at an angle 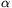 to the vertical. Does the relative change of length of the enclosed air column depend on
to the vertical. Does the relative change of length of the enclosed air column depend on 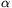 if the temperature is changing?
if the temperature is changing?
(3 pont)
solution (in Hungarian), statistics
P. 4206. The length of the newest Indian nuclear submarine is 112 m, its mass is 6000 tons, its maximum speed is 44 km/h and its maximum power is 85 MW. Using these data and the data in the table estimate the
a) maximum thrust of the submarine,
b) the diameter of the body of the submarine.
(4 pont)
solution (in Hungarian), statistics
P. 4207. Two tennis balls of mass 60 g are attached with a massless rubber thread, and held in the vertical position as shown in the figure. In this position the unstretched length of the rubber thread is 40 cm. The upper ball is slowly raised vertically upward, until the lower ball just becomes unsupported by the ground. At this time the length of the thread is 1 m. The rubber thread exerts a force which is proportional to its extension.
a) How much work is done while the upper ball was raised?
b) Releasing the upper ball at what speed will it hit the lower one?
c) How much time elapses between the release of the upper ball and the collision?
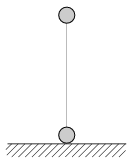
(5 pont)
solution (in Hungarian), statistics
P. 4208. Three marbles of mass 4m, m and 3m can slide without friction along a horizontal rod. (There are holes in the balls.) At a certain moment the middle marble is given an initial speed of v0=5 m/s towards the right. After the totally elastic collisions determine the
a) velocities of the marbles;
b) the ratio of the kinetic energies of the marbles.
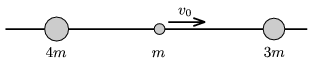
(4 pont)
solution (in Hungarian), statistics
P. 4209. As an average we take breath 18 times in every minutes, and approximately 500 cm3 is inhaled in each breath. The O2 content of the inhaled air is 21%, and that of the exhaled air is 16%. The temperature of the air in the lungs is the same as the body temperature.
How many grams of O2 is consumed in a day?
(4 pont)
solution (in Hungarian), statistics
P. 4210. 1 kg water of temperature 80 oC is poured onto 10 kg ice of temperature -30 oC which is in a thermally isolated container, and then 5 kg water vapour at a temperature of 120 oC is added.
What is the final state of the system?
(4 pont)
solution (in Hungarian), statistics
P. 4211. A current of I is flowing in a wire which is in the centre of an infinitely long straight metal tube. The radius of the tube is r the width of its wall is d (d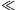 r), and the young modulus of its material is E. By what amount does the radius of the tube change if a current of magnitude I is started in the tube which current is opposite to the current in the wire. Does the radius increase or decrease?
r), and the young modulus of its material is E. By what amount does the radius of the tube change if a current of magnitude I is started in the tube which current is opposite to the current in the wire. Does the radius increase or decrease?
(5 pont)
solution (in Hungarian), statistics
P. 4212. The ratio of the components in a mixture, which consists of two elements, is to be determined. The atomic number of the elements are big, their atomic mass numbers are the same. and the amount of the sample is only 0.8 mg. We know that both elements 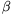 decay when they are bombarded by neutrons. They behave similarly when absorbing neutrons. The half-life of element A is half an hour and the half-life of element B is an hour. Right after the neutron irradiation the
decay when they are bombarded by neutrons. They behave similarly when absorbing neutrons. The half-life of element A is half an hour and the half-life of element B is an hour. Right after the neutron irradiation the 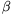 emission is measured. At this time -- subtracting the background -- 400 particles are measured in 10 seconds, and after an hour only 145 particles are measured during 10 seconds.
emission is measured. At this time -- subtracting the background -- 400 particles are measured in 10 seconds, and after an hour only 145 particles are measured during 10 seconds.
Determine the mass of the element A and the mass of the element B in the sample.
(5 pont)
solution (in Hungarian), statistics
P. 4213. It is often stated about the line spectrum of Hydrogen that the lines of the Lyman series is in the ultraviolate region, the lines of the Balmer series are in the region of visible light, and the lines of the Paschen and other series are in the infrared region. However, this is not exactly true, because not all the lines of the Balmer series can be seen by the naked eye.
Using the Bohr model of the atom find how many of the lines in the Balmer series belong to the region of visible light, and which are they?
(4 pont)
Upload your solutions above.
