A KöMaL 2015. májusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2015. június 10-én LEJÁRT. |
M. 351. Mérjük meg egy elektrolitkondenzátor ,,átvezetési'' ohmos ellenállását! Mennyire függ ez a rákapcsolt feszültségtől?
Közli: Vass Miklós, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2015. június 10-én LEJÁRT. |
P. 4736. Egy hajó a folyón az egyik hídtól a másik hídig halad, majd azonnal visszaindul. Az oda-vissza úthoz hányszor több időre van szüksége, mintha állóvízben haladna?
Közli: Tornyos Tivadar Eörs, Budapest
(3 pont)
P. 4737. Egy üvegprizma egyik lapjára merőlegesen beeső fénysugár a másik lapon \(\displaystyle 45^\circ\)-os törési szögben lép ki. Mekkora a prizma törőszöge, ha a fény sebessége ebben az üvegben 240000 km/s?
Közli: Holics László, Budapest
(3 pont)
P. 4738. Legalább mekkora sebességgel haladjunk el egy léckerítés mellett, hogy a kerítésen merőlegesen átszűrődő napfényt folytonosan lássuk? A lécek szélessége 5 cm, a réseké 10 cm. Az emberi szem az \(\displaystyle \frac 1{15}\) másodpercnél rövidebb ideig tartó képeket nem képes elkülönítve érzékelni.
Közli: Szász Krisztián, Budapest
(3 pont)
P. 4739. A világ egy olyan helyén, ahol a gravitációs gyorsulás pontosan \(\displaystyle 10~\rm{m/s}^2\), és semmi sem akadályozza a szabadesést, egy piros és egy zöld színű kő esik egymáshoz közeli függőleges pályán. A piros kő éppen akkor indul, amikor a magasabbról, ugyancsak kezdősebesség nélkül indított zöld kő a piros mellé ér. Kis idő múlva a két kő között 7 m a távolság, majd az innen számított 2 másodperc elteltével ez a távolság 27 m-re nő. Mennyivel magasabbról indult a zöld kő?
Szombathy Miklós (1940-2014) feladata
(4 pont)
P. 4740. Függőleges, alul zárt hengerben lévő súlytalan, súrlódásmentesen mozgó dugattyú alatt a külső légnyomással megegyező, \(\displaystyle p_0=10^5\) Pa nyomású, \(\displaystyle V_0=8~\rm dm^3\) térfogatú ideális gáz van. A dugattyút az \(\displaystyle A=2~\rm dm^2\) keresztmetszetű henger aljával egy \(\displaystyle D=1000\) N/m direkciós erejű rugó köti össze. Egy fizikai kísérlet során a hengeren lévő csapon keresztül a gáz tömegét 50%-kal, az abszolút hőmérsékletét pedig melegítéssel 60%-kal megnöveljük. Határozzuk meg a gáz térfogatát és nyomását a változások után!

Közli: Kotek László, Pécs
(4 pont)
P. 4741. A tengerparthoz közeli, magas hegy alján éppen ,,elfogy'' a 20 literes palackban a gáz. Ekkor a szelepet gyorsan elzárjuk, s felvisszük a palackot a hegy tetején lévő kutatóállomásra. Itt újra sikerül használni a gázt. Amikor itt is ,,kiürül'' a tartály, mérleggel megmérjük, s kiderül, hogy a hegy tetején használat közben 4,1 grammal csökkent a palack tömege. A hegy tetején a légnyomás 32 kPa-lal kisebb, mint a tengerszinten. A gáz hőmérséklete a hegy alján és a kutatóállomáson is \(\displaystyle 27~{}^\circ\)C, a levegő sűrűsége a tengerszinten 1,2 kg/m\(\displaystyle {}^3\).
\(\displaystyle a)\) Milyen gáz lehetett a palackban?
\(\displaystyle b)\) Milyen magas a hegy?
Közli: Simon Péter, Pécs
(4 pont)
P. 4742. Egy \(\displaystyle C\) kapacitású, feltöltött kondenzátor \(\displaystyle W\) elektromos energiát tárol. Ekkor egy második, töltetlen kondenzátort kapcsolunk hozzá párhuzamosan. Mekkorának válasszuk a második kondenzátor kapacitását ahhoz, hogy ez a kondenzátor az állandósult állapot beállta után a lehető legtöbb elektromos energiát tárolja?
E választás esetén mekkora lesz a két kondenzátorban tárolt összenergia?
Közli: Bilicz Sándor, Budapest
(4 pont)
P. 4743. Közös pontban felfüggesztett két egyenlő hosszú szigetelő fonál mindegyikén egy-egy kicsiny ebonitgolyó függ, melyeken azonos előjelű és nagyságú elektromos töltés van. A fonalak \(\displaystyle 2\alpha=60^\circ\) szöget zárnak be egymással, amikor az ingák egy edény belsejében, de levegőben vannak egyensúlyi helyzetben. Ezután az edény feltöltjük petróleummal annyira, hogy a golyók teljesen a petróleumban legyenek, távol az edény falától és a folyadék felszínétől. Mekkora lesz most a fonalak által bezárt szög?
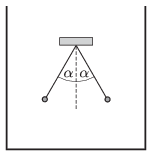
Adatok: Az ebonit sűrűsége \(\displaystyle 1200~{\rm kg}/{\rm m^3}\), a petróleumé \(\displaystyle 820~{\rm kg}/{\rm m^3}\). A petróleum relatív dielektromos állandója: \(\displaystyle \varepsilon_{\rm r}=2\).
Közli: Légrádi Imre, Sopron
(5 pont)
P. 4744. A \(\displaystyle B=0{,}02\) tesla indukciójú homogén mágneses térben ugyanazon \(\displaystyle B\)-vonalon két pont \(\displaystyle (X\) és \(\displaystyle Y)\) helyezkedik el egymástól 10 cm távolságra. Az \(\displaystyle X\) ponton egy 800 V feszültséggel felgyorsított elektron halad át, sebessége a \(\displaystyle B\)-vonallal \(\displaystyle \alpha\) szöget zár be. Mekkora lehet az \(\displaystyle \alpha\) szög, ha az elektron az \(\displaystyle Y\) ponton is áthalad?

Vermes Miklós (1905-1990) feladata
(5 pont)
P. 4745. Fizikaórán a decibel skáláról tanulnak a diákok. Egyikük megkérdezi a tanárt, hogy van-e maximális erősségű hanghullám. A tanár válasza: ,,Van! A hangerősség elméleti felső határa 194 dB.'' Hogyan kaphatjuk meg ezt a furcsa számértéket?
Közli: Honyek Gyula, Budapest
(5 pont)
P. 4746. A fény transzverzális hullám voltának bizonyítására szokás bemutatni a következő kísérletet:
Természetes fényből előállított keskeny, párhuzamos nyalábot ejtünk egy sík üveglapra olyan szögben, hogy a megtört és a visszavert fénysugár merőleges legyen egymásra. Az üveglapról visszaverődő fény útjába egy másik üveglapot helyezünk úgy, hogy a beesési szög itt is ugyanakkora legyen, mint az előbb. Ha ezt a második üveglapot a ráeső fénysugár mint tengely körül elforgatjuk, előállhat olyan eset, hogy erről már egyáltalán nem verődik vissza fénysugár.
\(\displaystyle a)\) Hogyan bizonyítja ez a kísérlet a fény transzverzális hullám voltát?
\(\displaystyle b)\) Mekkora beesési szöggel esik a fénysugár az üveglapokra, ha az üveg törésmutatója \(\displaystyle n=1{,}5\)?
\(\displaystyle c)\) Mekkora szöget zár be a két üveglap síkja egymással akkor, amikor a második üveglapról nem verődik vissza fénysugár?
Közli: Radnai Gyula, Budapest
(5 pont)
P. 4747. Egy 40 cm hosszúságú lánc két végpontját azonos magasságban rögzítjük az ábrán látható módon. Mekkora a lánc görbületi sugara

\(\displaystyle a)\) a legalsó pontjában,
\(\displaystyle b)\) a felfüggesztési pontokban?
Közli: Vigh Máté, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)
