KöMaL Problems in Physics, January 2017
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on February 10, 2017. |
M. 365. Measure the depth of water, at which a table-tennis ball is to be released in order that
\(\displaystyle a)\) the whole ball emerges from the water;
\(\displaystyle b)\) the ball emerges to the highest level above the water surface.
(6 pont)
 |
Problems with sign 'G'Deadline expired on February 10, 2017. |
G. 590. The vapour trail of air planes is formed not exactly at the planes, but some distance behind them, and follows the plane as if it was pulled by a rope. Why does this happen?
(3 pont)
solution (in Hungarian), statistics
G. 591. A journey from \(\displaystyle A\) to \(\displaystyle B\) takes 8 hours for a plane flying into a headwind, whilst the backward journey from \(\displaystyle B\) to \(\displaystyle A\) with tailwind takes 7 hours. If the wind speed is considered to be constant, by what factor is the speed of the air plane (without wind) greater than the wind speed?
(3 pont)
solution (in Hungarian), statistics
G. 592. A ball is dropped from a height of \(\displaystyle H\) and it collides totally elastically with a slant wall at a height of \(\displaystyle h<H\). The angle between the wall and the horizontal is \(\displaystyle 45^\circ\).
\(\displaystyle a)\) What should the height \(\displaystyle h\) be in order that the range (horizontal displacement) of the ball is to be the greatest?
\(\displaystyle b)\) What is this maximum range?
(3 pont)
 |
Problems with sign 'P'Deadline expired on February 10, 2017. |
P. 4894. Foucault, a French physicist, carried out his famous pendulum experiment in the Pantheon in Paris to demonstrate that the Earth is rotating, by means of a pendulum of length 67 m and of mass 28 kg.
\(\displaystyle a)\) Why was it necessary to use such a long wire and such a heavy pendulum bob?
\(\displaystyle b)\) What was the period of the pendulum?
(4 pont)
solution (in Hungarian), statistics
P. 4895. A rod of length \(\displaystyle \ell\), and of mass \(\displaystyle M\), and another rod of length \(\displaystyle 2\ell\), and mass \(\displaystyle 2M\) are arranged as shown in the figure. What is the direction and the magnitude of the gravitational force exerted on the point-like object of mass \(\displaystyle m\)? (Look for an elementary solution.)
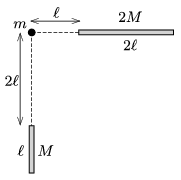
(5 pont)
solution (in Hungarian), statistics
P. 4896. A small sport plane makes a trip, first flying into a headwind, from \(\displaystyle A\) to \(\displaystyle B\) towards the north in 3 hours, whilst the backward trip from \(\displaystyle B\) to \(\displaystyle A\) flying with tailwind takes 2 hours. How long would the full trip (i.e., forth and back) take if the wind blew constantly from the northeast? (The speed of the wind can be considered as constant.)
(4 pont)
solution (in Hungarian), statistics
P. 4897. Water flows out through a tap at the bottom of a vertical cylindrical container, open at its top. The water level in the cylinder decreases at a certain speed. How does this speed change? If half of the water flows out in time \(\displaystyle T\), how long will it take to empty the full container?
(5 pont)
solution (in Hungarian), statistics
P. 4898. The arms of a U-shaped tube are vertical. The arm on the right side is closed and the other arm is closed by a moveable piston. There is mercury in the tube and initially the level of the mercury in the arms is the same. Above the mercury, there is an air column of height \(\displaystyle h\) in each arm, and the initial air pressure is the same as the atmospheric pressure in both arms. How much does the mercury level in each arm move if the piston is slowly pushed down by a distance of \(\displaystyle h/2\)?
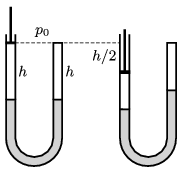
Data: \(\displaystyle h=30\) cm, and the atmospheric pressure is the same as the pressure of a mercury column of height \(\displaystyle H=76\) cm.
(4 pont)
solution (in Hungarian), statistics
P. 4899. The electric field lines of a vast region of uniform electric field are horizontal. The electric field strength is \(\displaystyle E=10^4\) N/C. At one point of this region a metal ball of mass \(\displaystyle m=4\) g is projected vertically upward at a speed of \(\displaystyle v_0=2\) m/s. Initially the metal ball was charged positively to a charge of \(\displaystyle q=3\cdot10^{-6}\) C.
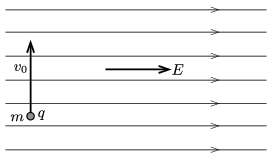
\(\displaystyle a)\) What is the displacement of the ball when its speed becomes the same as its initial speed was?
\(\displaystyle b)\) How much time elapses until this instant?
\(\displaystyle c)\) What is the minimum speed of the ball during its motion?
\(\displaystyle d)\) Where is the ball when it is the slowest?
(4 pont)
solution (in Hungarian), statistics
P. 4900. An interesting optical toy consists of two opposite concave spherical mirrors, having the same radius of curvature, the one at the top having a circular hole of diameter of a few centimetres at its centre. The distance between the mirrors is set in a way, that if a small object (e.g. a piece of candy) is placed at the centre of the mirror at the bottom, then its image is formed at the centre of the mirror with the hole in it. The light beam forms the image after a reflection first in the top, then in the bottom mirror.
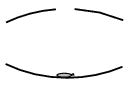
\(\displaystyle a)\) What is the distance between the centers of the two mirrors?
\(\displaystyle b)\) Is the image upright or inverted? Is it a virtual or a real image? What is the magnification?
(5 pont)
solution (in Hungarian), statistics
P. 4901. Joseph Fraunhofer, a German physicist, started his measurements in 1814 in order to investigate the spectrum of the Sun, and found 570 dark lines in the spectrum, which he denoted with letters (or sometimes letters with numbered indices). A particular diffraction grating has 500 gratings in 1 mm. Two images (formed symmetrically about the zeroth-order maximum) of one of the Fraunhofer lines are formed at a distance of 196.6 cm on the screen, which is at a distance of 3.6 m from the diffraction grating.
What is the wavelength of this spectral line and which Fraunhofer line is it?
(4 pont)
solution (in Hungarian), statistics
P. 4902. An initially neutral solid red copper ball of radius 5 cm, attached to an insulating handle, was charged by the negative terminal of a 5 kV voltage supply. (The positive terminal was earthed.) By what percent does the number of electrons of the copper ball increase?
(4 pont)
solution (in Hungarian), statistics
P. 4903. A small ball of mass \(\displaystyle m\) and of charge \(\displaystyle Q\) is attached to the bottom end of a piece of negligible-mass thread of length \(\displaystyle L\), whose top end is fixed. The system formed by the thread and the ball is in uniform magnetic field, \(\displaystyle \boldsymbol B\), which is perpendicular to the plane of the figure and points into the paper.
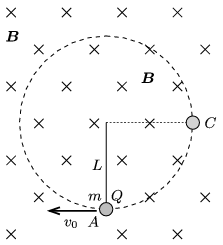
The ball is started in a direction perpendicular both to the magnetic induction and to the direction of the thread. At a certain initial speed the ball moves along a circular path such that the thread remains tight during the whole motion.
\(\displaystyle a)\) What is the magnitude of the magnetic induction \(\displaystyle B\) if the minimum initial speed at which the described motion of the ball occurs is \(\displaystyle v_0=\frac 12 \sqrt{17Lg}\,\)?
\(\displaystyle b)\) By what factor is the force acting on the thread at point \(\displaystyle A\) greater than that at point \(\displaystyle C\), when the initial speed of the ball is the above stated one?
(5 pont)
solution (in Hungarian), statistics
P. 4904. The initial voltage across the capacitor of capacitance \(\displaystyle C\), connected as shown in the figure is \(\displaystyle 2U_0\), whilst the capacitor of capacitance \(\displaystyle 2C\) is neutral.
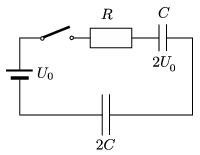
How much heat is dissipated at the resistor of resistance \(\displaystyle R\) after closing the switch?
(6 pont)
Upload your solutions above.
