Amit jó tudni a kúpszeletekről

A definícióban szereplő rögzített pontokat az adott görbe fókuszainak, a rögzített egyenest a parabola vezéregyenesének nevezzük. A továbbiakban a fókusz(oka)t F (és F₂), parabola esetén a vezéregyenest v, ellipszis és hiperbola esetén az állandó értékét pedig 2a jelöli. Ezt az értéket ellipszis esetén a nagytengely, hiperbola esetén pedig a valós tengely hosszának nevezzük.

Megmutatható, hogy ha egy mindkét irányban végtelen egyenes körkúpfelületet elmetszünk bármely olyan \(\displaystyle \mathcal{S}\) síkkal, amelyik nem megy át a kúp csúcsán és nem merőleges a kúp tengelyére, akkor a keletkezett metszetgörbe

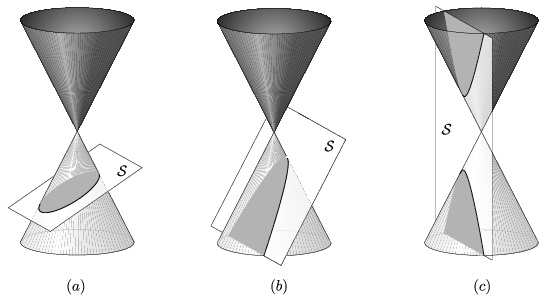
1. ábra

Ezt itt nem bizonyítjuk, a bizonyítás megtalálható pl. internetes honlapunkon [3]. Az is belátható, hogy minden kúpszelet előáll mint egy kúpfelület és egy megfelelő sík metszete. Ha azt is megengedjük, hogy a metsző sík merőleges legyen a kúp tengelyére, akkor a köröket is tekinthetjük a kúp szeleteinek. A kör tehát olyan elfajuló ellipszis, amelynél F\(\displaystyle \equiv\)F₂. Ezért a továbbiakban a kúpszelet összefoglaló nevet fogjuk használni az ellipszisre, körre, parabolára és hiperbolára.

A kúpszeletek \(\displaystyle \mathcal{S}\) pontjait három osztályba sorolják: A kúpszelet pontjai; \(\displaystyle \mathcal{S}\)-nek a forgáskúp belsejével alkotott metszete (2. ábra), amelyeket a kúpszeletre nézve belső pontokak nevezünk, valamint \(\displaystyle \mathcal{S}\) többi pontja, melyeket a kúpszeletre nézve külső pontoknak nevezünk.

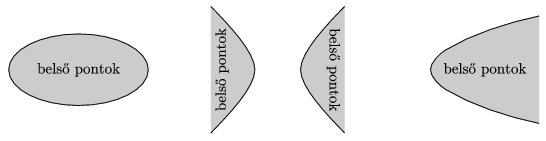
2. ábra

Ez az elnevezés összhangban van azzal, ahogy a kör belső, illetve külső pontjának fogalmát eddig használtuk. A külső és belső pontok jellemzéséről szól a következő tétel.

2. tétel. Legyen a kúpszelet a szokásos módon megadva. Ekkor a B pont belső pont, a G pont a görbén lévő pont, a K pont pedig külső pont akkor és csak akkor, ha

Bizonyítás. Elegendő bebizonyítani, hogy a belső és a külső pontokra teljesülnek a megfelelő egyenlőtlenségek, hiszen minden pont vagy rajta van a görbén, vagy külső pont, vagy pedig belső pont és a görbén lévő pontokra vonatkozó állítások az 1. definíció átfogalmazásai.

Kör esetén az állítás nyilvánvaló. Ellipszis és hiperbola esetén feltehetjük, hogy KF\(\displaystyle \le\)KF₂ és BF\(\displaystyle \le\)BF₂. Jelöljük az F-ből induló, B-t, illetve K-t tartalmazó félegyenes és a kúpszelet metszéspontját M-mel. Ekkor az MBF₂ és az MKF₂ (esetleg elfajuló) háromszögekre felírt háromszög-egyenlőtlenségekből ellipszis esetén (3.(a). ábra)

BF+BF₂ <BF+BM+MF₂=MF+MF₂=2a < MF+MK+KF₂=KF+KF₂,

hiperbola esetén (3.(b). ábra) pedig

BF₂-BF >(MF₂-MB)-BF=MF₂-MF=2a > (KF₂-KM)-MF=KF₂-KF

adódik, ami éppen a bizonyítandó állítás.

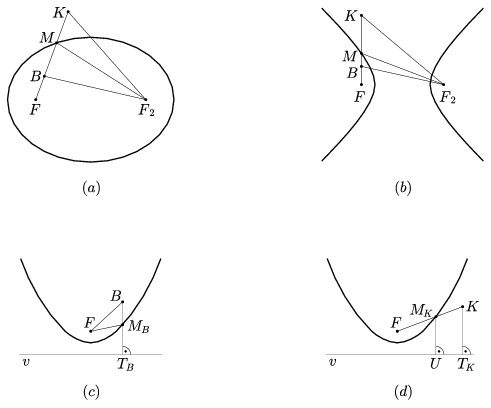
3. ábra

Parabola esetén legyen M_B a B-ből v-re állított merőleges és a görbe metszéspontja, M_K az F-ből induló K-t tartalmazó félegyenes és a görbe metszéspontja, a B-ből, K-ból és M_K-ból v-re állított merőlegesek talppontjai pedig rendre T_B, T_K és U (3.(c), (d). ábrák). Ekkor az M_BBF és az M_KKU (esetleg elfajuló) háromszögekre felírt háromszög-egyenlőtlenségekből kapjuk a bizonyítandó

FB<BM_B+M_BF=BM_B+M_BT_B=BT_B és FK=FM_K+M_KK=M_KU+M_KK>KU \(\displaystyle \ge\)KT_K

egyenlőtlenségeket.  \(\displaystyle \square\)

A kör érintője olyan egyenes, amelynek egy közös pontja van a körrel, összes többi pontja pedig külső pont. Ezért természetes módon adódik a következő definíció:

3. definíció. Az e egyenes a \(\displaystyle \mathcal{K}\) kúpszeletet annak E pontjában érinti, ha e átmegy E-n és összes többi pontja \(\displaystyle \mathcal{K}\)-nak külső pontja.

Következő állításunk szemléletesen nyilvánvaló.

4. tétel. Legyen a \(\displaystyle \mathcal{K}\) kúpszelet tetszőleges pontja E. Ekkor egyértelműen létezik \(\displaystyle \mathcal{K}\)-t E-ben érintő egyenes.

Bizonyítás. Állítsuk elő \(\displaystyle \mathcal{K}\)-t az O csúcsú \(\displaystyle \mathcal{F}\) kúp és az \(\displaystyle \mathcal{S}\) sík metszeteként. Ekkor minden E-n átmenő \(\displaystyle \mathcal{S}\)-beli f egyeneshez egyértelműen hozzárendelhetjük azt az OE alkotóra illeszkedő \(\displaystyle \mathcal{S}_f\) síkot, mely tartalmazza f-et is és OE-t is. Nyilvánvaló, hogy az \(\displaystyle \mathcal{S}_f\) sík pontosan annyi alkotóját tartalmazza \(\displaystyle \mathcal{F}\)-nek, ahány közös pontja van f-nek és \(\displaystyle \mathcal{K}\)-nak. Az OE alkotóra illeszkedő síkok közt pontosan egy van, amelyik az OE alkotóban érinti \(\displaystyle \mathcal{F}\)-et, az összes többi pedig egy-egy O-n átmenő egyenespárban metszi azt. Mivel az érintősíknak nincs pontja \(\displaystyle \mathcal{F}\) belsejében, ezért az általa \(\displaystyle \mathcal{S}\)-ből kimetszett egyenes lesz \(\displaystyle \mathcal{K}\) egyértelműen létező E-beli érintője.  \(\displaystyle \square\)

Vezéralakzatok

Az ezután következő definíciók és tételek mind síkbeliek, ezért ezt külön nem is fogjuk hangsúlyozni. Kezdjük egy nyilvánvaló állítással.

5. lemma. Legyenek O₁ és O₂ különböző pontok. Ekkor az O₁ középpontú, r₁ sugarú és az O₂ középpontú, r₂ sugarú körök

(a) akkor és csak akkor érintik egymást kívülről, ha r₁+r₂=O₁O₂;

(b) akkor és csak akkor érintik egymást belülről, ha |r₁-r₂|=O₁O₂;

(c) akkor és csak akkor metszik egymást két pontban, ha az r₁,r₂ és O₁O₂ szakaszokból háromszög szerkeszthető (4. ábra).

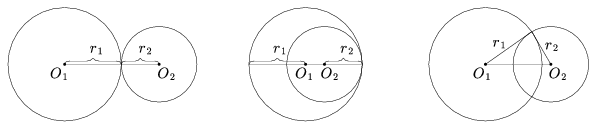
4. ábra

A kúpszeletek egységes, síkbeli előállításáról szól a következő tétel.

6. tétel. Adott az F pont és a rajta át nem menő v alakzat, ami vagy kör vagy egyenes. Azon körök középpontjainak halmaza, amelyek átmennek F-en és érintik v-t, kúpszelet. Speciálisan ez a görbe

Bizonyítás. Legyen k egy F-en átmenő, v-t az E pontban érintő r sugarú kör, P pedig k középpontja.

Először tegyük fel, hogy v egyenes (5. ábra). Mivel a kör érintője merőleges az érintési pontba húzott sugárra, ezért PE merőleges v-re. Tehát P és v távolsága megegyezik PE hosszával, és mivel PE=r=PF, ezért P rajta van az F fókuszú, v vezéregyenesű parabolán.

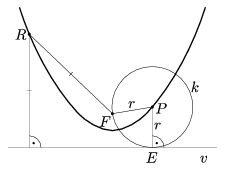
5. ábra

Másrészt ha R ennek a parabolának tetszőleges pontja, akkor R és v távolsága éppen RF, azaz az R-ből v-re állított merőleges talppontja rajta van v-n, tehát az R középpontú RF sugarú körnek v érintője.

Ha v kör, akkor jelöljük a középpontját F₂-vel, sugarának hosszát pedig 2a-val.

Tegyük most fel, hogy F a v belső pontja (6. ábra). Ekkor az 5. lemma (b) része szerint 2a=EF₂=EP+PF₂=PF+PF₂. Vagyis ha F\(\displaystyle \equiv\)F₂, akkor P rajta van az F középpontú a sugarú körön, ha pedig F és F₂ különbözőek, akkor P rajta van az F és F₂ fókuszú, 2a nagytengelyű ellipszisen.

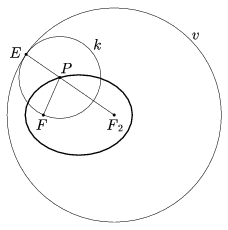
6. ábra

Másrészt ha R ennek a körnek vagy ellipszisnek tetszőleges pontja, akkor RF+RF₂=2a. Ezért ha az F₂-ből kiinduló F₂R félegyenesre F₂-ből felmért 2a hosszú szakasz másik végpontja G, akkor RG=2a-PF₂=RF, tehát az R középpontú RF sugarú kör G-ben érinti v-t.

Végül tegyük fel, hogy F a v kör külső pontja. Ekkor k helyzete kétféle lehet: vagy tartalmazza v-t (7. ábra), vagy pedig kívülről érinti azt (8. ábra). Az 5. lemma (a), illetve (b) része szerint mindkét esetben igaz, hogy

|PF-PF₂|=|PE-PF₂|=F₂E=2a,

tehát P rajta van az F és F₂ fókuszú, 2a valós tengelyű hiperbolán.

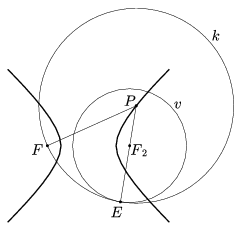
7. ábra

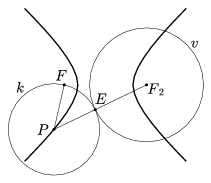
8. ábra

Másrészt ha R ennek a hiperbolának tetszőleges pontja, akkor vagy RF=RF₂+2a, vagy pedig RF₂=RF+2a. Ezért v az első esetben belülről, a második esetben pedig kívülről érinti az R középpontú RF sugarú kört.  \(\displaystyle \square\)

Tételünk alapján beszélhetünk az F fókuszú, v vezéralakzatú kúpszeletről. Ha v kör, akkor a továbbiakban középpontját mindig F₂-vel, sugarának hosszát pedig 2a-val jelöljük. Ellipszis és hiperbola esetén F és F₂ a görbe két fókusza. Az 1. definícióból következően a görbe szimmetrikus az FF₂ szakasz felező merőlegesére. Ha v-t tükrözzük erre az egyenesre, akkor az F középpontú, 2a sugarú v₁ kört kapjuk. Ezért az F₂ fókuszú, v₁ vezérkörű kúpszelet megegyezik az F fókuszú, v vezérkörű kúpszelettel. Általában v-t az F₂ fókuszhoz, v₁-et pedig az F fókuszhoz tartozó vezérkörnek nevezik. Ellipszis és hiperbola esetén a további állításaink akkor is igazak, ha F-et F₂-vel és ugyanakkor v-t v₁-gyel helyettesítjük.

A vezéralakzatok segítségével a külső és belső pontokat is egyszerűen jellemezhetjük.

7. tétel. Legyen \(\displaystyle \mathcal{K}\) egy F fókuszú, v vezéralakzatú kúpszelet. Ekkor a P pont \(\displaystyle \mathcal{K}\) külső pontja pontosan akkor, ha a P középpontú PF sugarú kör két pontban metszi v-t, belső pontja pedig pontosan akkor, ha a P középpontú PF sugarú körnek és v-nek nincs közös pontja.

Bizonyítás. Ha \(\displaystyle \mathcal{K}\) parabola, akkor v egyenes. A P középpontú PF sugarú kör pontosan akkor metszi két pontban v-t, ha P v-től való távolsága kisebb mint a PF távolság, és pontosan akkor kerüli el v-t, ha P v-től való távolsága nagyobb mint a PF távolság.

Ha \(\displaystyle \mathcal{K}\) kör, akkor az állítás nyilvánvaló. Ha \(\displaystyle \mathcal{K}\) ellipszis vagy hiperbola, akkor az 5. lemma (c) része szerint a v kör, melynek középpontja F₂, sugara 2a, és a P középpontú, PF sugarú körök akkor és csak akkor metszik egymást két pontban, ha a 2a,PF és PF₂ szakaszokból szerkeszthető háromszög.

Ellipszis esetén FF₂<2a, ezért PF+2a>PF+FF₂\(\displaystyle \ge\)PF₂ és PF₂+2a>PF₂+FF₂\(\displaystyle \ge\)PF mindig teljesül. Tehát két metszéspont van, ha PF+PF₂>2a, és nincs metszéspont, ha PF+PF₂<2a. Ez viszont a 2. tétel szerint éppen a bizonyítandó állítás.

Hiperbola esetén FF₂>2a, ezért PF+PF₂\(\displaystyle \ge\)FF₂>2a mindig fennáll. Tehát két metszéspont van, ha PF<PF₂+2a és PF₂<PF+2a is teljesül, azaz ha |PF-PF₂|<2a. Ha pedig |PF-PF₂|>2a, akkor nincs metszéspont. Ez ismét a 2. tétel miatt adja a bizonyítandó állítást.  \(\displaystyle \square\)

Az egységes tárgyalás kedvéért bevezetünk néhány szokásos elnevezést. A továbbiakban azt mondjuk, hogy egy kör és egy egyenes merőleges egymásra, ha az egyenes átmegy a kör középpontján. Ha G a \(\displaystyle \mathcal{K}\) kúpszelet tetszőleges pontja, akkor az FG, továbbá a G-ből v-re állított merőleges egyeneseket a G-hez tartozó vezérsugaraknak nevezzük. (Parabola kivételével tehát a másik vezérsugár az F₂G egyenes.) A kúpszelet minden pontjában egyértelműen létezik érintő egyenes a 4. tétel szerint. Az érintő és a vezérsugarak kapcsolatáról szól a következő tétel.

8. tétel. A \(\displaystyle \mathcal{K}\) kúpszelet tetszőleges G pontjában az érintő felezi a G-hez tartozó vezérsugarak szögét.

Bizonyítás. Legyen \(\displaystyle \mathcal{K}\) az F fókusszal és a v vezéralakzattal adva. A 6. tétel szerint a G középpontú GF sugarú kör érinti v-t. Jelöljük az érintési pontot E-vel és legyen g az FGE\(\displaystyle \angle\) belső szögfelezője. Ekkor parabola és hiperbola esetén g a G-hez tartozó vezérsugarak belső-, ellipszis és kör esetén pedig azok külső szögfelezője (9. ábra).

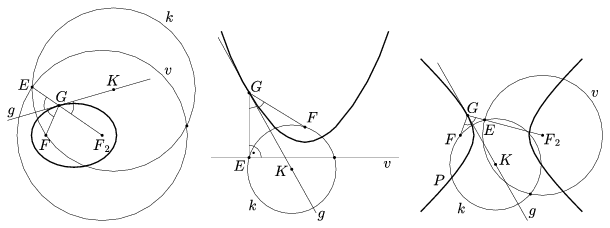
9. ábra

Elegendő megmutatnunk, hogy a g egyenes G-től különböző, tetszőleges K pontja külső pont. Mivel K rajta van az FGE\(\displaystyle \angle\) szögfelezőjén, azért KF=KE. Tehát a K középpontú KF sugarú k kör átmegy E-n, ami v-n van. Mivel K különbözik G-től, azért k nem érinti, hanem metszi v-t. Ez viszont a 7. tétel szerint azt jelenti, hogy K külső pont.  \(\displaystyle \square\)

Miután a G-beli érintőről beláttuk, hogy az az FGE\(\displaystyle \angle\) belső szögfelezője, azonnal adódik a következő állítás.

9. következmény. A kúpszelet fókuszának a kúpszelet tetszőleges érintőjére való tükörképe rajta van a vezéralakzaton.  \(\displaystyle \square\)

A kúpszelet tengelyének nevezzük a fókuszból a vezéralakzatra állított merőlegest. Ha a kúpszeletet a tengelye körül megforgatjuk, akkor a keletkezett felületet ellipszoidnak, paraboloidnak, illetve hiperboloidnak nevezzük.

A 8. tételt ellipszisre alkalmazva kapjuk, hogy ha az egyik fókuszból sugarakat indítunk, akkor azok a visszaverődési törvény szerint az ellipszoid felületéről visszaverődve a másik fókuszon fognak áthaladni. Ezt a jelenséget figyelhetjük meg pl. a Csodák Palotájában akkor, amikor a megfelelő helyen, az egyik fókuszban halkan elmondott szavainkat a tőlünk távol, de jó helyen, a másik fókuszban álló ismerősünk tökéletesen hallja.

Parabola esetén pedig az következik tételünkből, hogy a parabola tengelyével párhuzamosan érkező sugarak a visszaverődés után áthaladnak a fókuszon. A műholdas adások vételére szolgáló antennák alakja ezért paraboloid, s a jeleket fogó fej a fókuszban helyezkedik el.

Érintők

A 9. következmény szerint csak olyan egyenes lehet az F fókuszú, v vezéralakzatú kúpszelet érintője, mely merőlegesen felezi a v valamely pontját F-fel összekötő szakaszok egyikét. A következő tétel alapján egyszerűen megszerkeszthetjük egy kúpszelet adott ponton átmenő, illetve adott egyenessel párhuzamos érintőit.

10. tétel. Legyen \(\displaystyle \mathcal{K}\) F fókuszú, v vezéralakzatú kúpszelet, P tetszőleges pont, e pedig tetszőleges egyenes.

Legyenek a P középpontú, PF sugarú kör és v közös pontjai E₁ és E₂. Ekkor \(\displaystyle \mathcal{K}\) P-n átmenő érintői megegyeznek a PE₁ és a PE₂ szakaszok felező merőlegeseivel (10.(a). ábra).

Legyenek az F-en átmenő, e-re merőleges egyenes és v metszéspontjai E₁ és E₂. Ekkor \(\displaystyle \mathcal{K}\) e-vel párhuzamos érintői megegyeznek az FE₁ és az FE₂ szakaszok felező merőlegeseivel (10.(b), (c). ábrák, ellipszis, ill. parabola).

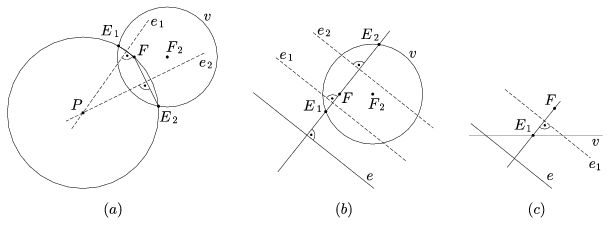
10. ábra

Bizonyítás. A két részállítás bizonyítása szóról-szóra megegyezik.

A 9. következmény miatt más, P-n átmenő, illetve e-vel párhuzamos egyenes nem lehet érintő.

Legyen az FE_i (i=1,2) szakasz felezőmerőlegese e_i, az e_i és az E_i-ben v-re állított merőleges egyenes metszéspontja pedig G_i. Ekkor G_iF=G_iE_i, tehát a G_i középpontú, G_iF sugarú kör érinti v-t, azaz G_i rajta van \(\displaystyle \mathcal{K}\)-n. Viszont az e_i egyenes felezi az FG_iE_i szöget, tehát a 8. tétel szerint G_i-ben érinti \(\displaystyle \mathcal{K}\)-t.  \(\displaystyle \square\)

Tételünk első részéből következik az a szemléletesen nyilvánvalónak tűnő állítás, hogy ha P külső pont, akkor P-n \(\displaystyle \mathcal{K}\)-nak két érintője megy át. Ez azonban csak egy kis kiegészítéssel igaz. A bizonyítás során megkonstruált G_i érintési pontok ugyanis nem mindig léteznek. Előfordulhat, hogy az E_i-ben v-re állított merőleges párhuzamos FE_i felező merőlegesével. Parabola esetén ez nem lehetséges, ekkor ugyanis FE_i sohasem párhuzamos v-vel. A többi kúpszelet esetén FE_i felezőmerőlegese pontosan akkor párhuzamos az E_i-ben v-re állított merőlegessel, azaz az E_iF₂ egyenessel, ha FE_iF₂\(\displaystyle \angle\)=90^o. Ez csak akkor állhat elő, ha F a v-nek külső pontja, azaz \(\displaystyle \mathcal{K}\) hiperbola, és az FE_i egyenes érinti v-t. Ekkor az F-ből v-hez húzott két érintőszakasz felezőmerőlegeseit a hiperbola aszimptotáinak (11. ábra) nevezzük.

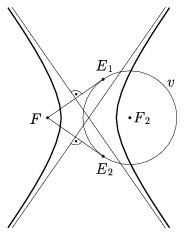
11. ábra

Minden hiperbolának két aszimptotája van. Sok szempontból célszerű ezeket az egyeneseket is a hiperbola érintőinek tekinteni, a továbbiakban mi is ezt tesszük. (Szemléletesen azt mondhatjuk, hogy a hiperbolát a ,,végtelen távoli pontjában'' érinti az aszimptota. Ez a kijelentés a projektív geometria eszközeivel teljesen precízzé tehető, lásd pl. [1] 44. és 46. fejezet.) Ha tehát a P külső pont a hiperbola egy vagy két aszimptotáján rajta van, akkor P-n az aszimptotákkal együtt megy át két érintő.

Az adott irányú érintőből ellipszis és kör esetén mindig kettő van, hiszen a v kör belsejében lévő F ponton átmenő e-re merőleges egyenes két különböző E_i pontban metszi v-t, s mivel FE_iF₂\(\displaystyle \angle\)<90^o, azért a G_i pontok is mindig létrejönnek (10.(b). ábra).

Parabola esetén az e-re merőleges egyenesnek és v-nek legfeljebb egy közös pontja van, hiszen v is egyenes (10.(c). ábra). A vezéregyenesre merőleges irányt kivéve mindig létezik is pontosan egy, adott irányú érintő, mert ekkor az E és a G pontok mindig létrejönnek. A vezéregyenesre merőleges irányú érintője viszont nincs a parabolának.

Hiperbola esetén az F-en átmenő, e-re merőleges egyenes pontosan akkor metszi két pontban v-t, ha az FF₂ szakasz felezőpontján átmenő, e-vel párhuzamos e' egyenes az aszimptoták által meghatározott négy szögtartomány közül abba a kettőbe metsz bele, melyek nem tartalmazzák a hiperbola pontjait. Ekkor viszont a G_i pontok is létrejönnek, tehát ilyen irányú érintőkből mindig kettő van (12. ábra).

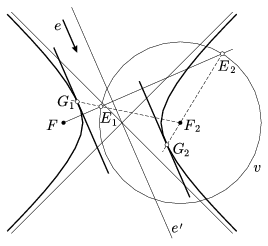
12. ábra

Irodalom

[1] Hajós György: Bevezetés a geometriába, 6. kiadás, Tankönyvkiadó (Budapest, 1979).

[2] Horvay Katalin és Reiman István: Geometriai feladatok gyűjteménye, I. kötet, 4. kiadás, Tankönyvkiadó (Budapest, 1976).

[3] Kós Rita: Kúpszeletek és Dandelin-gömbjeik

[4] Rácz János: Paraboláról, hiperboláról elemi geometriai eszközökkel, II. rész, KöMaL, 34. évf. (1984), 193-199.

[5] Schopp János: Kúpszeletek, Középiskolai szakköri füzetek, Tankönyvkiadó (Budapest, 1972).

Kiss György
(A T043556 és T043758 számú OTKA
pályázatok támogatásával.)

A cikk II. része