Számadó László
A statisztika alapjai
1. Alapfogalmak
A gazdaság és a társadalom vizsgálatánál nagyon sok résztvevőt kell áttekintenünk. Nem tehetjük meg, hogy minden résztvevő összes sajátosságát számon tartsuk. Általában csak néhány számadat áll rendelkezésünkre ahhoz, hogy kérdéseinket megválaszoljuk. Ezek a számadatok igen változatosak lehetnek. Közvetlen környezetünkben is találhatunk példákat ,,árulkodó'' számokra: a következő évben hány tanuló jár iskolába, ezek száma hogyan oszlik meg területenként, milyen magasak a tanulók stb.
A tömegesen előforduló jelenségek és folyamatok számbavételével, az így nyert adatok vizsgálatával, elemzésével foglalkozik a statisztika. A statisztikus először adatokat gyűjt a vizsgálat tárgyát képező egyedekről, az úgynevezett statisztikai sokaság elemeiről. Az információgyűjtés során vizsgált tulajdonságot ismérvnek nevezik.
2. Népszámlálás
Egy országban a legszélesebb körben végzett információgyűjtés a népszámlálás. Hazánkban 2001. február 1-től 21-ig tartott az utolsó népszámlálás. "Mindenki számít", ez volt az alapgondolata ennek az óriási feladatnak, amikor az ország "apraját, nagyját" számbavették. A válaszaival ilyenkor mindenki hozzájárul a népszámlálás sikeréhez, a személyes adatokat pedig bizalmasan, a törvényi előírásoknak megfelelően kezelik és dolgozzák fel.A lakosság előzetesen tájékoztatást kapott a legfontosabb kérdésekről, amely szórólap formájában is eljutott az emberekhez.
Mi a népszámlálás?
Ez az a folyamat, amikor az állam egy adott időpontra vonatkoztatva számba veszi az ország valamennyi lakosát, lakásukat, életkörülményüket, és egyéb információkat is gyűjt róluk.
Miért szükséges a népszámlálás?
Azért, hogy tudjuk hányan és milyenek vagyunk. Fontos tudni például, hány óvodai, iskolai férőhelyre lesz szükség a jövőben, hány lakás építése, hány munkahely kialakítása szükséges. A kapott eredmények alapján összehasonlítást végezhetünk, megtudhatjuk helyünket a világban. Vagyis a népszámlálás során fontos információkhoz jutunk, amelyek a társadalmi és gazdasági élet számára is hasznosak.
Mióta beszélhetünk népszámlálásról?
Amióta az emberiség államokba szerveződve él, fontosnak érezték, hogy számbavegyék a népességet. Az ókorban Kínában számlálták meg az embereket először, Rómában a hadra foghatóság miatt volt fontos tudni a polgárok számát. A mai népszámlálások célja az adatok biztosítása a társadalom és a gazdaság számára.
Hazánkban II. József uralkodása idején zajlott az első mai értelemben vett népszámlálás. Az 1870-es népszámlálást az akkor létrehozott Központi Statisztikai Hivatal végezte. Azóta évtizedenként rendszeresen felmérik az ország teljes lakosságát.
Mi a szerepe a Központi Statisztikai Hivatalnak?
A Központi Statisztikai Hivatal megalakulása óta szervezi hazánkban a népszámlálásokat, így a sikeres lebonyolításhoz több mint 130 éves tapasztalattal rendelkezik. Hasznos és szükséges információkhoz juttatja a hivatal a központi és helyi igazgatási szervezeteket, az üzleti életben dolgozókat, a kutatókat, az állampolgárokat, biztosítja a nemzetközi összehasonlíthatóságot.
Mi a statisztika feladata?
A statisztika feladata és célja, hogy valósághű, tárgyilagos képet adjon a társadalom, a gazdaság, a környezet állapotáról, változásairól.
3. Statisztikai adatok ábrázolása
A fenti tájékozódás fontos számunkra. Természetesen a népszámlálásnál kisebb méretű adatsokasággal (mintával) találkozunk gyakrabban. Egy városra, községre, iskolára vagy csak egy osztályra vonatkozó adatokkal rendszeresen találkozhatunk mindennapjainkban.
1. példa
Nézzük meg egy osztály matematika dolgozatának eredményeit. Végezzünk adatgyűjtést, az adatokat rögzítsük táblázatban.
Az egyes adatok előfordulásának számát gyakoriságnak nevezzük. A statisztikai adatsokaságot célszerűen leírjuk, a lehetséges értékeket gyakoriságukkal együtt egy táblázatban foglaljuk össze. Ezt nevezzük gyakorisági eloszlásnak. Itt a statisztikai sokaságot az osztály tanulói alkotják, az ismérv pedig az érdemjegy lesz. A gyűjtött adatok alapján például a következő táblázat készülhetett:
|
A fenti táblázatból nem olvasható ki, hogy egy konkrét tanuló milyen jegyet kapott. Erre most nincs is szükségünk.
Ha nagy mennyiségű adat alapján szeretnénk következtetni, lényeges, hogy az adatokat ,,könnyen olvashatóvá'' tegyük. Az 1. példában a gyakorisági eloszlás táblázata sokkal áttekinthetőbb volt, mintha felsoroltuk volna a dolgozatra kiosztott jegyeket. Vannak azonban ennél szemléletesebb módszerek is. A média (újságok, TV, internet stb.) igényli is a gyorsan áttekinthető ábrázolásokat. Gyakran csak néhány pillanat van egy statisztikai felmérés közlésére. Egy nagyobb táblázatot, amit képernyőn mutatnak a legjobb szemű néző sem tud átlátni. Azonban egy színes ábrára, úgynevezett diagramra tett pillantás nagyon sok mindent elárulhat arányokról, a változás esetleges irányáról. (És ha megfelelő módon van elkészítve, manipulálhatja is a nézőt, lásd pl. a 11. feladatot.)
Az ábrázoláshoz használható az oszlopdiagram, a kördiagram, a grafikon stb. A leggyakrabban használt típusokat egy-egy példán mutatjuk be.
2. példa
Ábrázoljuk az 1. példában szereplő adatokat több lehetséges módon.
a) A koordinátarendszer vízszintes tengelyén az öt osztályzatot fogjuk megjeleníteni, a függőleges tengelyén a darabszámot.
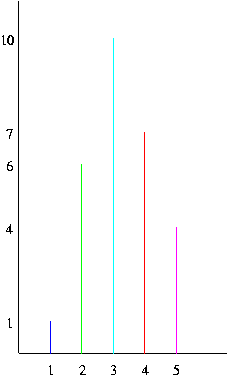
Természetesen az így kapott pontokat nem köthetjük össze. Csak a dolgozatot írt 28 diák eredményeit ábrázoltuk ezen az ábrán.
b) A koordinátarendszer vízszintes tengelyén most is az öt osztályzatot fogjuk megjeleníteni, a függőleges tengelyén pedig a darabszámot. Az előző ábránál szemléletesebb képet kapunk, ha téglalapokat rajzolunk a vízszintes tengelyre. Az így kapott ábrát oszlopdiagramnak nevezzük. A következő ábrán ezt a lehetőséget használtuk az adatok ábrázolására.
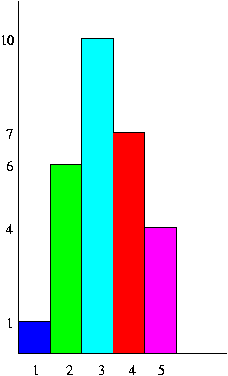
Az így kapott képen jól látható a maximum és a minimum, a különbségeket is könnyen le tudjuk olvasni. Ezt a típust akkor célszerű használni, ha az adatok egymáshoz való nagyságrendjét szeretnénk szemléltetni. Most is csak a dolgozatot írt 28 diák eredménye szerepel az ábrán.
c) A kördiagram készítésénél a körcikkek középponti szöge arányos lesz az adatfajta gyakoriságával. Ez az ábrázolási mód kifejezően szemlélteti az arányokat.
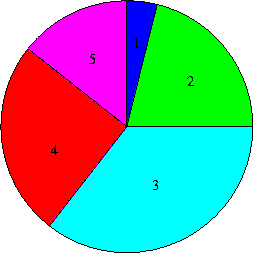
d) Egy téglalap (vagy négyzet) megfelelő nagyságú részével is megjeleníthetők az eredmények.
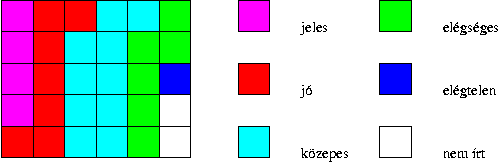
Most a dolgozatot nem írt tanulók számát is megjelenítettük az ábrán. Mivel csak 30 adatot kellet ábrázolnunk, így most kényelmes volt egy 5-ször 6-os téglalapot használni. Nagyobb adatsokaság esetén egy 10-szer 10-es négyzet segítségével könnyen és gyorsan megjeleníthetők a százalékok.
Természetesen további szemléletes ábrázolási lehetőségek is vannak, mi nem vállalkozhatunk az összes típus bemutatására.
Feladatok
1. Dobjunk egy dobókockával 36-szor. Készítsünk a dobásokról táblázatot, amely a
gyakorisági eloszlást mutatja. Ábrázoljuk oszlopdiagram és kördiagram segítségével az
adatokat.
A feladat megoldása.
2. Dobjunk két dobókockával 36-szor. Készítsünk a dobások összegéről táblázatot, amely a
gyakorisági eloszlást mutatja. Ábrázoljuk oszlopdiagram és kördiagram segítségével az
adatokat.
A feladat megoldása.
3. Egy gimnázium 9. évfolyamán négy osztály tanul. A következő táblázatból megtudjuk a fiúk és a lányok számát. Oszlopdiagramon ábrázoljuk ezeket az adatokat.
|
4. Ábrázoljuk a földrészek területét. Az adatokat 1000 km2-re kerekítettük.
| Afrika | 30 284 |
| Amerika | 42 078 |
| Antarktisz | 13 328 |
| Ausztrália és Óceánia | 8 557 |
| Eurázsia | 54 381 |
5. Gyűjtsünk a napilapokból, folyóiratokból grafikonokat, táblázatokat. Elemezzük,
értelmezzük a látottakat.
A feladat megoldása.
4. Statisztikai mutatók
A statisztikai sokaság mérete általában nagy, ezért fontos, hogy néhány számmal jól tudjuk jellemezni az összegyűjtött adatokat. Az ilyen számokat statisztikai mutatóknak nevezik.
a) Középértékek
A közepekkel már találkozhattunk az iskolai tanulmányaink során. A számtani közép helyett sokszor átlagot szoktunk mondani, de a hétköznapi szóhasználatban az "átlagos", a "közepes" elnevezéseknek más jelentése is lehet.
Átlag
A legismertebb statisztikai mutató a számtani közép, amit átlagnak is nevezünk.
Definíció: A számsokaság összegét elosztjuk a számsokaság darabszámával, ekkor a számsokaság átlagát vagy számtani közepét kapjuk.
3. példa
Számítsuk ki az 1. példában szereplő osztály tanulói által írt matematika dolgozatok eredményének számtani közepét.
Számoljuk ki először a jegyek összegét:
4.5+7.4+10.3+6.2+1.1=91.
Összesen 28 tanuló írt dolgozatot, így a számtani közép: 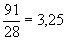 .
.
A kiszámított számtani középben az elért eredmények "elvesztek". Az adatsokaságból egy jellemzőt, egy statisztikai mutatót számítottunk ki. Ez ,,csupán" egy szám, de ez mégis sokat elárul az adatokról. Az átlaggal mindenki gyakran találkozik a mindennapi életben is. Tudjuk, hogy máshogyan kell értékelni négyes dolgozatunkat, ha 2,35, illetve ha 4,61 az osztály átlaga.
4. példa
Ennek a cikknek az 1. bekezdése alapján vizsgáljuk meg, hogy hány betűből áll egy átlagos magyar szó.
A cikk 1. bekezdésében 62 szó van. A gyakorisági táblázat a betűk száma alapján:
|
Ha számtani közepet veszünk, akkor össze kell adnunk a 62 szó összes betűjét. A betűk száma 413. Osztunk a szavak számával, így a számtani közép 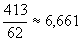 .
.
A válaszunk a következő lehetne: Egy átlagos magyar szó 6,661 betűből áll.
Ebben a példában adott válaszunkban zavaró lehet, hogy 6,661 betűből álló szó nem is létezik, hiszen nem egész számot kaptunk. Ez az egyik ok, amiért érdemes lenne más értelmezést is találni. A másik ok pedig az, hogy csak az esetek egy részében lesz az adatsokaságra valóban jellemző az átlaga, bizonyos esetekben viszont másik középértéket lesz érdemesebb használni.
Módusz
A táblázatból jól látható, hogy a hat betűs szavakból van a legtöbb a szövegben. Ezért a fenti sokaság újabb jellemzőjének nevezzük a 6-ot.
Definíció: A számsokaságban legtöbbször előforduló számot a számsokaság móduszának nevezzük.
A módusz akkor használható, ha az adatok közül kiemel egyet, nem szerencsés a használata, ha több adat is közel azonos gyakorisággal emelkedik ki a sokaságból.
Medián
Nézzük meg a szavakat a betűk száma szerint sorrendbe rendezve. Először az 5 darab 1 betűs, aztán a 2 darab 2 betűs stb. szavak következnek. A 62. helyen van az 1 darab 16 betűs szó. Középre a 31. és a 32. szó került, mindkettő 6 betűből áll. Ez is egy fontos statisztikai mutató.
Definíció: Rendezzük nagyság szerint sorba a számadatokat. A középsőt nevezzük mediánnak (ha két középső van, akkor ezek átlagát vesszük).
Látható, hogy ugyanannyi adat nem nagyobb a mediánnál, mint amennyi nem kisebb.
Az átlag, a módusz és a medián összefoglaló neve: középértékek.
Feladatok
6. Készítsünk gyakorisági eloszlást arról, hogy az osztályban ki hányas cipőt hord. Ha egy
cipőboltban az osztály minden tanulója vásárolt 1 pár cipőt, akkor melyik méret fogyott a
legjobban? Ez melyik a tanult középértékek közül?
A feladat megoldása.
7. Gyűjtsünk adatokat arról, hogy a személygépkocsikban hányan utaznak. Készítsünk egy
rövid elemzést a rendelkezésünkre álló adatok alapján a személygépkocsik kihasználtságáról.
Az elemzésben szerepeljenek statisztikai mutatók.
A feladat megoldása.
8. Néhány anyától megkérdeztük, hogy hány éves korában született az első gyermeke. A
következő válaszokat kaptuk:
25; 22; 32; 23; 37; 24; 27; 25; 28; 23; 20; 26; 23; 27; 34; 29; 22; 32; 23; 23; 19; 20; 39; 20; 27;
24; 29; 23; 24; 25.
Határozzuk meg a móduszt, a mediánt és az átlagot. Tegyünk fel egy-egy kérdést, amelyre
ezekkel a középértékekkel kell válaszolni.
A feladat megoldása.
9. Valaki szeretne elhelyezkedni egy cégnél, de nem tudja milyen fizetésre számíthat. Az ott
dolgozó emberek fizetéseinek melyik középértékét érdemes megkérdezni?
A feladat megoldása.
10. Egy osztályban a lányok testmagasságának átlaga 168 cm, a fiúké pedig 174 cm. Az
osztályban 16 lány és 14 fiú van. Számítsuk ki az osztály testmagasságának átlagát.
A feladat megoldása.
11. Hat tantárgy átlagát számolta ki egy osztály osztályfőnöke, magyar irodalom 3,52,
történelem 3,74, matematika 3,96, fizika 3,61, kémia 3,56 és biológia 3,72 lett. Ábrázoljuk
ezeket az eredményeket,
a) ha szülői értekezleten szeretné megmutatni és hangsúlyozni a tanár, hogy a tanulók a
különböző tantárgyakban viszonylag egyenletesen teljesítenek;
b) ha az iskola igazgatójának szeretné megmutatni és hangsúlyozni a tanár, hogy az
osztály matematikából kiugróan jó a többi tantárgyhoz képest.
A feladat megoldása.
12. a) Három tanulónak három tantárgyból elért félévi eredményeit vizsgáltuk. Először
kiszámoltuk mindegyikük átlagát, majd az átlagok átlagát vettük. Másodszor kiszámoltuk a
három tantárgy átlagát, majd ezen átlagok átlagát is meghatároztuk. A kapott két érték milyen
viszonyban lehet egymással?
b) Válaszoljunk az előző kérdésre n tanuló és k tantárgy esetén.
A feladat megoldása.
13. Egy matematika tanár tanít a 9. A és a 9. B osztályban is. Íratott egy közös dolgozatot,
ahol 60 pont volt a maximum. Az A osztályban 42 pont, a B osztályban 37 pont lett az átlag.
Az A osztályos fiúk átlagosan 40,5, a B osztályos fiúk pedig 35,5 pontot értek el. Az A
osztályban a lányok átlagosan 45, míg a B-ben a lányok 38 pontos dolgozatot írtak. Mennyi a
két osztályban az összes lány átlagpontszáma, ha tudjuk, hogy a fiúké 39,5?
A feladat megoldása.
14. Tudjuk, hogy hat számnak a mediánja 5. Mit mondhatunk a mediánról, ha a hat számhoz
hozzávesszük a 6-ot is?
A feladat megoldása.
b) Szóródás
5. példa
A megadott osztályzatok alapján számítsuk ki az alábbi három tanuló jegyeinek átlagát, móduszát és mediánját:
|
A kért statisztikai mutatókat fejben is könnyen kiszámolhatjuk. Az eredményeket táblázatba foglaltuk:
|
Mindegyik esetben mindhárom középérték 3, pedig az adatsokaságok eltértek egymástól. A sokaságok jellemzésére nem elegendő középértékeket használni, ezért bevezetjük a szóródást mérő számokat.
Terjedelem
A legegyszerűbb mérőszám, amivel a minta szórtságát jellemezhetjük a terjedelem.
Definíció: A számsokaság legnagyobb és legkisebb számának különbségét terjedelemnek nevezzük.
A terjedelmet egyszerűen meg tudjuk határozni, ezért gyakran használjuk. Hátránya, hogy egyetlen szélsőséges adat már nagyon befolyásolja ezt a mérőszámot. (Az ilyen szélsőséges adatokat például egyes pontozásos sportágakban úgy küszöbölik ki, hogy nem számítják a legkisebb és a legnagyobb pontszámot.) Az 5. példa esetén az adatsorokhoz a következő terjedelmek tartoznak: az 1. tanulóhoz 0, a 2. tanulóhoz 2, a 3. tanulóhoz 4.
Átlagos abszolút eltérés
A statisztikában használatos szóródás mérőszám lehet az átlagos abszolút eltérés.
Definíció: Az
x1;x2;...;xn
számsokaság egy tetszőleges x számtól vett átlagos
abszolút eltérésének nevezzük a következőt:
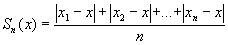
6. példa
Az 5. példában szereplő három tanuló osztályzatainak határozzuk meg az átlagtól és a mediántól vett átlagos abszolút eltérését.
Az 1. tanuló jegyeinek átlaga és mediánja is 3, ezért most ugyanaz lesz az átlagtól és
a mediántól vett átlagos abszolút eltérés:
S11(3)=0.
A 2. tanulónál is 3 az átlag és a medián is. Használjuk a közölt képletet: 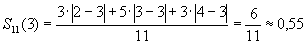
A 3. tanuló átlaga és mediánja is 3. A képletet használva:
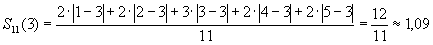 .
.
Láttuk, hogy a középértékek megegyeztek a három sokaság esetén, de az átlagos abszolút eltérések (0; 0,55; 1,09) már mutatják az adatsorok közötti különbözőséget.
Megmutatható, hogy az átlagos abszolút eltérés a mediántól a legkisebb, az Sn(medián) számot a sokaság átlagos minimális eltérésének nevezzük. Általában az átlagtól vett eltéréssel szoktunk dolgozni, így mi röviden ezt fogjuk átlagos abszolút eltérésnek nevezni.
Átlagos négyzetes eltérés és szórás
Belátható, hogy a négyzetösszegek jobban jellemzik a sokaság szerkezetét, ezért használják a szóródás jellemzésére az átlagos négyzetes eltérést a statisztikában.
Definíció: Azx1;x2;...;xn
számsokaság egy tetszőleges x számtól vett átlagos
négyzetes eltérésének nevezzük a következőt:
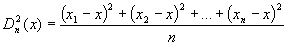
Ha x pontosan a sokaság átlaga, akkor ezt a számot a sokaság szórásnégyzetének nevezzük, a belőle vont négyzetgyököt pedig szórásnak.
Megmutatható, hogy D2n(x) akkor minimális, ha x a sokaság átlaga. Ezeket a mérőszámokat már néhány szám esetén is hosszadalmas kiszámítani. A zsebszámológépek általában rendelkeznek a statisztikai funkciókkal, ezek a lehetőségek gyorsítják a munkánkat.
7. példa
Az 5. példában szereplő három tanuló osztályzatainak határozzuk meg a szórását.
Az 1. tanuló jegyeinek átlaga 3, így a szórás:
D11(3)=0.
A 2. tanulónál is 3 az átlag. Használjuk a szórás meghatározására közölt képletet:
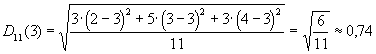
A 3. tanuló átlaga is 3. Használjuk ismét a képletet:
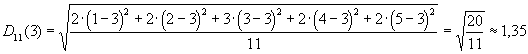
Az így kapott három statisztikai mutató az 1. tanulónál 0, a 2. tanulónál 0,74, a 3. tanulónál pedig 1,35.
Feladatok
15. Az előző héten három tanuló jegyeit figyeltük meg. Andrásé: 3, 5, 4; Bálinté: 3, 5, 3, 4, 4;
Csabáé: 2, 1, 3, 5, 4. Számítsuk ki a szórást mind a három adatsor esetén.
A feladat megoldása.
16. Két adatsor a következő: 1, 2, 2, 2, 3, 4, 5, 6, 7, 8 illetve 5, 6, 6, 6, 7, 8, 9, 10, 11, 12.
Melyik adatsornak nagyobb az (átlagtól vett) átlagos abszolút eltérése?
A feladat megoldása.
17. Egy szakkör 5 tanulójának magasságát jelölje x1;x2;x3;x4;x5.
Határozzuk meg az
f(x)=|x1-x|+|x2-x|+|x3-x|+|x4-x|+|x5-x|
hozzárendelésű függvény minimum helyét.
A feladat megoldása.
18. Jelölje egy 4 fős társaság tagjainak testtömegét x1;x2;x3;x4.
Határozzuk meg az
f(x)=(x1-x)2+(x2-x)2+(x3-x)2+(x4-x)2
hozzárendelésű függvény minimum helyét.
A feladat megoldása.
Zárszó helyett
Ez a néhány oldal a statisztika alapfogalmaival ismertette meg az olvasót. Röviden mindenről olvashattunk, ami a 9. osztályos tantervben szerepel. A példákat, a feladatokat is úgy válogattam, hogy a tantervhez illeszkedők legyenek. Természetesen különböző nehézségűek, de az iskolai tudássál és az itt olvasottak felhasználásával megoldhatók. A cikk alapjául szolgált a Bolyai János Matematikai Társulat által szervezett Rátz László Vándorgyűlésen (Miskolc, 2001. július 3-6.) elhangzott előadásom, valamint a Hajnal- Számadó-Békéssy Matematika 9. a gimnáziumok számára (Nemzeti Tankönyvkiadó, 2001) tankönyv.
További feladatok
19. Egy osztályban 13 leány és 13 fiú írt matematika dolgozatot.
| A leányok érdemjegyei: | 5, 5, 2, 1, 3, 4, 2, 2, 4, 3, 3, 4, 4. |
| A fiúk érdemjegyei: | 3, 1, 2, 1, 4, 2, 2, 4, 3, 3, 4, 1, 4. |
A lányoknak az a véleménye, hogy ők jobban szerepeltek. A fiúk azt hangoztatják, hogy összességében nem rosszabbak a dolgazataik, mint a lányoké. Az osztály egyetért abban, hogy nem lett rossz ez a dolgozat. A matematikatanáruk szerint "csapnivaló" az eredmény.
a) Számítsuk ki az osztály átlagát.
b) Számítsuk ki a lányok és a fiúk átlagát külön-külön.
c) Mennyi az osztályra vonatkoztatott medián?
d) Határozzuk meg külön a lányok és külön a fiúk eredményeinek mediánját.
e) Mennyi az osztályban a módusz?
f) Határozzuk meg a lányok és a fiúk eredményeinek móduszát.
g) Rövid indoklással támasszuk alá a négy véleményt. Használjunk statisztikai mutatókat az érvelésünkhöz.
A feladat megoldása.
20. Egy iskola igazgatói állására hárman adták be pályázatukat: Sándor (S), József (J) és Benedek (B). A 48 fős tantestület minden tagja felállította az alkalmassági sorrendet. Ezeket összeszámoltuk:
| az S, J, B sorrendet | 14, |
| az S, B, J sorrendet | 5, |
| a J, S, B sorrendet | 6, |
| a J, B, S sorrendet | 9, |
| a B, S, J sorrendet | 4, |
| a B, J, S sorrendet | 10 |
a) Írjunk az adatok felhasználásával egy rövid beszédet, amelyben Sándor megköszöni,
hogy a tantestület neki szavazott bizalmat, ő a győztes.
b) Írjunk az adatok felhasználásával egy rövid beszédet, amelyben József megköszöni,
hogy a tantestület ilyen erősen őt támogatja, és ő lehet az iskola igazgatója.
c) Írjunk az adatok felhasználásával egy rövid beszédet, amelyben Benedek kifejti, hogy
miért szükséges a pályázatok alapos elolvasása után új szavazást tartani.
A feladat megoldása.
21. Egy megállóban a következő táblázat tájékoztatja az utasokat a munkanapok közlekedési menetrendjéről:
|
a) Határozzuk meg a nap első és utolsó járatát.
b) Az első és az utolsó járat között mikor kell a legtöbbet várakozni?
c) Hány perc a legrövidebb követési idő?
d) Hány járat van egy nap?
e) A nap hányad részében mondhatjuk, hogy biztosan nem kell fél óránál többet várakozni a
megállóban? Adjuk meg százalékban is ezt.
f) A nap hányad részében mondhatjuk, hogy biztosan nem kell 5 percnél többet várakozni a
megállóban? Adjuk meg százalékban is ezt.
g) A táblázatban kétszer is megjelennek a többihez képest hosszabb sorok. Adjunk
magyarázatot, miért lehet ez így?
h) Hogyan lehetne értelmezni és kiszámítani az átlagos vagy közepes követési időt?
i) Tervezzük meg a hétvégi menetrendet.
A feladat megoldása.
Fogalomtár
Adatsokaság (számsokaság, minta): A statisztikai elemzésekhez összegyűjtött adatokat így is szoktuk nevezni.
Átlag (számtani közép): A számsokaság összegét elosztjuk a számsokaság darabszámával.
Átlagos abszolút eltérés: Az x1;x2;...;xn
számsokaság egy tetszőleges x számtól vett átlagos
abszolút eltérésének nevezzük a következőt: 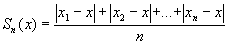 .
Általában x-nek a számsokaság átlagát szoktuk választani.
.
Általában x-nek a számsokaság átlagát szoktuk választani.
Átlagos minimális eltérés: Megmutatható, hogy az átlagos abszolút eltérés a mediántól a
legkisebb. Az x1;x2;...;xn számsokaságnak az M mediántól vett átlagos abszolút eltérését
nevezzük így, vagyis: 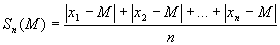 .
.
Átlagos négyzetes eltérés: Az x1;x2;...;xn
számsokaság egy tetszőleges x számtól vett
átlagos négyzetes eltérésének nevezzük a következőt: 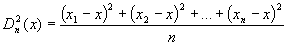 .
.
Gyakoriság: Az egyes adatok előfordulásának száma.
Gyakorisági eloszlás: A statisztikai adatsokaságban előforduló lehetséges értékeket a gyakoriságukkal együtt gyakorisági eloszlásnak nevezzük.
Gyakorisági táblázat: A statisztikai adatsokaságban előforduló lehetséges értékeket a gyakoriságukkal együtt egy táblázatba rendezzük.
Ismérv: Így nevezzük az információgyűjtés során vizsgált tulajdonságot.
Középértékek: Az átlag, a módusz és a medián összefoglaló neve.
Medián: Rendezzük nagyság szerint sorba a számsokaságot. A középsőt nevezzük mediánnak (ha két középső van, akkor ezek átlagát vesszük).
Minta (számsokaság, adatsokaság): A statisztikai elemzésekhez összegyűjtött adatokat így is szoktuk nevezni.
Módusz: A számsokaságban legtöbbször előforduló szám.
Statisztika: A tömegesen előforduló jelenségek és folyamatok számbavételével, az így nyert adatok vizsgálatával, elemzésével foglalkozó tudomány.
Statisztikai mutatók: A statisztikai sokaság mérete általában nagy, ezért fontos, hogy néhány számmal jól tudjuk jellemezni az összegyűjtött adatokat. Az ilyen jellemzésre alkalmas számokat hívjuk így.
Statisztikai sokaság: A statisztikai vizsgálat tárgyát képező egyedek összesége.
Számsokaság (minta, adatsokaság): A statisztikai elemzésekhez összegyűjtött adatokat így is szoktuk nevezni.
Számtani közép (átlag): A számsokaság összegét elosztjuk a számsokaság darabszámával.
Szórás: A szórásnégyzetből vont négyzetgyök.
Szórásnégyzet: Ha az átlagos négyzetes eltérés képletében x pontosan a számsokaságnak az átlaga akkor a szórásnégyzetet kapjuk.
Terjedelem: A számsokaság legnagyobb és legkisebb számának különbsége.

