Csatár Katalin - Harró Ágota - Hegyi Györgyné - Lövey Éva - Morvai Éva - Széplaki Györgyné - Ratkó Éva:
VALÓSZÍNŰSÉGSZÁMÍTÁS FELADATOK Kezdőknek
2. rész
1. rész 2. rész 3. rész 4. rész 5. rész 6. rész 7. rész
És akkor jöjjenek a feladatok
1. Egy szabályos dobókockával egyszer dobunk. Milyen esemény valószínűsége lehet az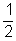 , a
, a 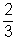 , illetve az
, illetve az  érték?
érték?
Megoldás:
P(a dobott szám prím) =
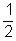
P(a dobott szám 3-mal nem osztható) =
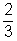
P(a dobott szám 3-mal osztható) =
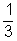
2.
 Egy dodekaéder lapjaira ráírtuk a számokat 1-12-ig. Mekkora a valószínűsége, hogy
Egy dodekaéder lapjaira ráírtuk a számokat 1-12-ig. Mekkora a valószínűsége, hogy
- a dobott szám 4-gyel osztható,
- a dobott szám 3-mal osztható,
- a dobott szám 4-gyel és 3-mal osztható,
- a dobott szám 4-gyel vagy 3-mal osztható,
- a dobott szám sem 3-mal, sem 2-vel nem osztható,
- a dobott szám jegyeinek összege legfeljebb 4,
- a dobott szám nem négyzetszám?
Megoldás:
- A tizenkét számból három osztható 4-gyel : 4, 8,12.
P =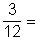
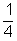
- A tizenkét számból négy osztható 3-mal : 3, 6, 9, 12 .
P =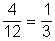
- Csak a 12 osztható 3-mal és 4-gyel, tehát
P =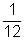
- Azt már láttuk, hogy három 4-gyel, illetve négy 3-mal osztható szám van a tizenkét szám között. A kettőt összeadva azt kapjuk, hogy 4+3=7 olyan szám van, ami 4-gyel vagy 3-mal osztható. De a 12-t kétszer is beleszámoltuk, ezért valójában csak 7-1=6 ilyen szám van. Vagyis
\(\displaystyle P={6\over12}={1\over2}\) - Nem osztható sem 2-vel, sem 3-mal az 1, az 5, a 7 és a 11, ezért
P =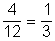
- A számjegyek összege legfeljebb 4 az 1,a 2, a 3, a 4, a 10, a 11 és a 12 számoknál, ezért
P =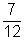
- Négyzetszámok az 1, a 4, a 9 , a többi kilenc nem az, tehát
P =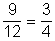

3. Fanni a zsebében lévő két szem citromos és két szem málnás cukorkából kivesz kettőt. Mekkora a valószínűsége annak,
hogy különböző ízűek?
Megoldás:
A négy cukorkából kettőt 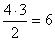 módon lehet kiválasztani. Ezekből nekünk
két eset nem felel meg: ha a két citromosat, vagy a két málnásat választja. Ezek valószínűsége
módon lehet kiválasztani. Ezekből nekünk
két eset nem felel meg: ha a két citromosat, vagy a két málnásat választja. Ezek valószínűsége 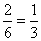 .
A többi négy esetben különböző a két cukor íze. Ennek a valószínűsége:
.
A többi négy esetben különböző a két cukor íze. Ennek a valószínűsége: 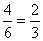 . (Ezt így is megkaphattuk volna: 1 -1/3 = 2/3.)
. (Ezt így is megkaphattuk volna: 1 -1/3 = 2/3.)

4. Két tálban 10-10 darab alma van, mindegyikben egy sárga, a többi piros. Bekötött szemmel választunk egy-egy almát mindkét tálból.
- Mekkora a valószínűsége annak, hogy a két sárgát választjuk?
- Mekkora a valószínűsége annak, hogy egy sárgát és egy pirosat választunk?
- Mekkora a valószínűsége annak, hogy legalább az egyik választott alma piros?
Megoldás:
- Annak a valószínűsége, hogy az egyik tálból a sárga almát választjuk 0,1. A két tálból egymástól függetlenül választunk, ezért annak a valószínűsége, hogy mindkét tálból a sárgát vesszük ki 0,1×0,1=0,01.
- Annak a valószínűsége, hogy az egyik tálból a sárga almát választjuk 0,1; annak, hogy a pirosat 0,9. A sárga almát vagy az első, vagy a második tálból választhatjuk, ezért a két különböző színű alma választásának valószínűsége: 0,1×0,9+0,9×0,1=2×0,1×0,9=0,18.
- Ha legalább az egyik alma piros, akkor vagy az egyik piros és a másik sárga, vagy mindkettő piros. Annak a valószínűsége, hogy az egyik választott alma piros, a másik pedig sárga a b. feladat szerint 0,18. Annak a valószínűsége, hogy mindkét választott alma piros 0,9×0,9=0,81. Így annak a valószínűsége, hogy legalább az egyik választott alma piros: 0,18+0,81=0,99. Ugyanerre az eredményre jutunk, ha azt mondjuk, hogy akkor nem lenne egy piros alma sem, ha mind a kétszer sárgát választunk. Tehát P(legalább az egyik piros)=1-P(mindkettő sárga)=1-0,01=0,99.
5. Az  számkártyákat összekeverjük, majd egymás után letesszük az
asztalra. Mekkora a valószínűsége annak, hogy az így kirakott négyjegyű szám
számkártyákat összekeverjük, majd egymás után letesszük az
asztalra. Mekkora a valószínűsége annak, hogy az így kirakott négyjegyű szám
- páratlan,
- hárommal osztható,
- néggyel osztható?
Megoldás:
A négy számkártyát 4×3×2×1=24 különböző sorrendben tudjuk egymás után letenni.
- Akkor páratlan, ha 1-re vagy 3-ra végződik, ez a 24 lehetséges eset fele, vagyis a valószínűsége 0,5.
- A számjegyek összege 1+2+3+4=10, azaz egyik szám sem lesz hárommal osztható, a valószínűség 0.
- Akkor osztható néggyel, ha az utolsó két számjegy 12 vagy 24 vagy 32. Mindhárom esetben a maradék két számjegy
kétféle sorrendben állhat elöl, tehát a kedvező esetek száma 2×3=6. A valószínűség tehát
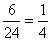 .
.

6. Két dobókockával dobunk egyszerre és összeadjuk a dobott számokat. Tomi arra fogad, hogy az összeg 6 lesz, Laci arra, hogy az összeg 7 lesz, Feri pedig arra, hogy az összeg 8 lesz. Melyiküknek van nagyobb esélye a nyerésre?
Megoldás:
Két kockával egyszerre dobva 6×6=36 a lehetséges esetek száma. Ebből a 36-ból kell kiválasztanunk azokat, amelyeknél
a dobott számok összege 6, vagy 7, vagy 8.
Az 1; 2; 3; 4; 5; 6 számokból a 6 is, a 7 is és a 8 is háromféle módon állítható elő két szám összegeként:
| 6 = 1+5 | 7 = 1+6 | 8 = 2+6 |
| 6 = 2+4 | 7 = 2+5 | 8 = 3+5 |
| 6 = 3+3 | 7 = 3+4 | 8 = 4+4 |
Amikor a két összeadandó azonos, akkor a jelöletlen és a jelölt kockán is ugyanaz a szám áll, vagyis ez az eset egyféleképpen jöhet létre.
Amikor a két összeadandó különböző, akkor két lehetőség van: a jelölt kockán van az első összeadandó és a jelöletlenen a második, vagy fordítva.
Így a hat 2+2+1=5, a hét 2+2+2=6, a nyolc 2+2+1=5 esetben jöhet létre a 36 lehetséges esetből. Ezért a tippelt összegek valószínűsége:
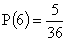 |
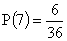 |
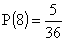 |
(Egy dobókocka szemközti lapjain mindig 7 a számok összege. Tehát, ha 1 áll fölül, akkor 6 alul; ha 5 fölül, akkor 2 alul. Így az 1+5 összegnek megfeleltethető egy 2+6 összeg. Ugyanígy bármelyik 6-os összegnek megfeleltethető egy 8-as összeg; így látható, hogy ugyanannyiféleképpen lesz az összeg 6, mint 8.)
7. Két dobókockával dobunk. Mennyi a valószínűsége annak, hogy a dobott számok
- szorzata 12,
- szorzata prímszám?
Megoldás:
Az egyik kockával is hatféle számot dobhatunk, a másikkal is, ezért összesen 6 × 6 = 36 elemi esemény lehetséges.
- 12 = 2 × 6
6 × 2
3 × 4
4 × 3
A szorzat négyféleképpen állhat elő , ezért P( a szorzat 12 ) =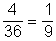 .
.
- A szorzatok között három prímszám van, a 2, a 3 és az 5. Mindegyik kétféleképpen jöhet ki:
2 = 2×1= 1×2, 3 = 3×1 = 1×3, 5 = 5×1= 1×5, ez 6 eset.
Tehát P( a szorzat prímszám) =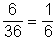 .
.
8. Két dobókockával dobunk. Adjunk meg olyan elemi eseményeket, amelyek valószínűsége
a. 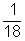 |
b. 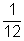 |
c. 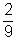 |
d. 1 |
Megoldás:
- P(a dobott számok összege 3) =
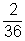 =
= 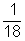
- P(a dobott számok összege páros négyzetszám) =
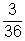 =
= 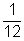
- P(a dobott számok összege 5-nél nagyobb prímszám) =
 =
= 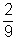
- P(a dobott számok szorzata legfeljebb 36) = 1
9.  Balázs és Marci testvérek. Esténként négy dobókocka feldobásával döntik el, ki sétáltatja másnap reggel a kutyát.
Négy kockával dobnak egyszerre. Ha a négy szám között van hatos, akkor Balázs, különben Marci sétáltatja másnap a kutyát.
Igazságos-e ez a módszer?
Balázs és Marci testvérek. Esténként négy dobókocka feldobásával döntik el, ki sétáltatja másnap reggel a kutyát.
Négy kockával dobnak egyszerre. Ha a négy szám között van hatos, akkor Balázs, különben Marci sétáltatja másnap a kutyát.
Igazságos-e ez a módszer?
Megoldás:
Egy kockadobás eredménye hatféle lehet: 1; 2; 3; 4; 5; 6.
Marci akkor sétáltatja a kutyát, ha nem dobnak hatost, vagyis a dobások eredménye az 1; 2; 3; 4; 5 számok közül kerül ki.
Így annak a valószínűsége, hogy egy dobás nem hatos 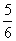 .
.
Annak a valószínűsége, hogy a négy kocka egyikén sincs hatos, vagyis hogy Marci sétáltatja reggel a kutyát:
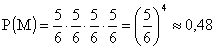
Minden más esetben van 6-os a dobások között, tehát P(B) = 1-P(M)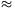 0,52.
0,52.
Tehát kicsivel nagyobb a valószínűsége annak, hogy Balázs sétáltatja reggel a kutyát, mint annak, hogy Marci: a
módszer nem igazságos.
10. Öt dobókockával dobunk egyszerre. Mekkora annak a valószínűsége, hogy három kockán lesz páros szám, kettőn pedig páratlan?
Megoldás:
A dobókocka oldalain ugyanannyi páros szám van, mint páratlan, ezért ugyanakkora eséllyel gurul páros számra, mint
páratlanra.
A kockák egymástól függetlenül gurulnak, ezért az összes lehetséges eset 25 = 32, hiszen minden kocka vagy páros,
vagy páratlan számot mutat.
Feltéve, hogy két kocka mutat páros, három páratlan számot, a következő lehetőségek adódnak:
|
Ez tíz eset a 32-ből, tehát a valószínűség
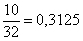
|

11. Egy fiókban van hat pár kesztyű.
- Csukott szemmel kiveszünk belőle két darabot. Mekkora a valószínűsége annak, hogy két jobbkezes kesztyűt választunk?
- A hat pár kesztyűből kivettünk két darab jobbkezest, majd a maradékból megint húzunk két darabot csukott szemmel. Mekkora a valószínűsége annak, hogy két balkezest választunk?
Megoldás:
- 6 db jobbkezes és 6 db balkezes kesztyű van a fiókban. Közülük kettőt
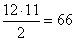 lehetséges módon tudunk kiválasztani. Nekünk az a kedvező, ha mindkét kesztyű a jobbkezesek közül kerül ki.
Ez
lehetséges módon tudunk kiválasztani. Nekünk az a kedvező, ha mindkét kesztyű a jobbkezesek közül kerül ki.
Ez 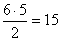 esetben fordulhat elő.
Így két jobbkezes kesztyű kiválasztásának valószínűsége:
esetben fordulhat elő.
Így két jobbkezes kesztyű kiválasztásának valószínűsége: 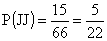 .
.
- Most 4 db jobbkezes és 6 db balkezes kesztyű van a fiókban. Közülük kettőt
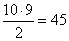 lehetséges módon tudunk kiválasztani. Most az a kedvező, ha mindkét kesztyű a balkezesek közül kerül ki.
Ez
lehetséges módon tudunk kiválasztani. Most az a kedvező, ha mindkét kesztyű a balkezesek közül kerül ki.
Ez 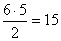 esetben fordulhat elő.
esetben fordulhat elő.
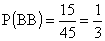 .
.
12. Feldobunk először egy 20 forintost és egy 50 forintost egyszerre, majd két 10 forintost. Mennyi az egyes esetekben
a valószínűsége annak, hogy mindkettő érmén fej lesz, mindkettőn írás lesz, illetve az egyiken fej, a másikon írás lesz?
Megoldás:
Az első esetben a következő lehet a dobás kimenetele:
| 20 Ft-os | 50 Ft-os | |
| FEJ | FEJ | |
| FEJ | ÍRÁS | |
| ÍRÁS | FEJ | |
| ÍRÁS | ÍRÁS |
A négy lehetséges esetből a FEJ-FEJ, illetve az ÍRÁS-ÍRÁS egy-egy esetben, a FEJ-ÍRÁS két esetben jön létre. A keresett valószínűségek tehát: P(FF) = P(ÍÍ) = 0,25 és P(FÍ) = 0,5.
A második esetben az egyik 10 forintost megjelölve ugyanazt a feladatot kapjuk, mint az első esetben. A
valószínűségek: P(FF) = P(ÍÍ) = 0,25 és P(FÍ) = 0,5.
13.
Karesz pénztárcájában 5 db 20 Ft-os van. Édesanyja betett a húszasok mellé néhány 10 Ft-ost is. Hány db tízest
kapott Karesz, ha ezek után a pénztárcájából találomra kiválasztott érme 0,8 valószínűséggel 10 Ft-os?
Megoldás:
Ha édesanyja x db 10 Ft-ost tesz a pénztárcába, akkor x + 5 db érem lesz benne.
Így P(10-est választunk) = 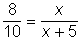 innen x = 20, tehát Karesz édesanyja 20 db 10 Ft-ost tett a pénztárcába.
innen x = 20, tehát Karesz édesanyja 20 db 10 Ft-ost tett a pénztárcába.
14. Vettünk öt darab egyforma Blend-a-med Complete és egy Blend-a-med Soda Bicarbonate fogkrémet. A szatyorban kicsúsztak a dobozukból. Hazaérve találomra beletettünk mindegyik dobozba egy-egy tubus fogkrémet.
- Mekkora a valószínűsége annak, hogy mindegyik dobozban a feliratnak megfelelő fogkrém van?
- Mekkora a valószínűsége annak, hogy pontosan öt dobozban van a feliratnak megfelelő fogkrém?
- Mekkora a valószínűsége annak, hogy pontosan négy dobozban van a feliratnak megfelelő fogkrém?
Megoldás:
- Ha a Blend-a-med Soda Bicarbonate fogkrém a saját dobozába kerül, akkor a többi is a feliratnak megfelelő helyen lesz. Ha a Blend-a-med Soda Bicarbonate
fogkrém nem kerül a saját dobozába, akkor a többi sem mind, hiszen az egyik Blend-a-med fogkrém a Blend-a-med Soda Bicarbonate dobozába
kerül. Tehát annak a valószínűsége, hogy mindegyik dobozban a feliratnak megfelelő fogkrém van, megegyezik annak a
valószínűségével, hogy a Blend-a-med Soda Bicarbonate fogkrém a saját dobozában van, ez pedig
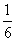 .
.
- Ha pontosan öt dobozban van a feliratnak megfelelő fogkrém, akkor már csak egy doboz és egy fogkrém maradt, így az utolsó fogkrémet csak a helyére tudjuk tenni. Vagyis 0 annak a valószínűsége, hogy pontosan öt dobozban van a feliratnak megfelelő fogkrém.
- Ha a Blend-a-med Soda Bicarbonate fogkrém a saját dobozába kerül, akkor a többi is a feliratnak megfelelő helyen lesz, ezért ez nem
lehet a helyén, hanem Blend-a-med-es dobozban van. Ekkor egy tubus Blend-a-med nincs jó helyen, a többi igen. Így annak
a valószínűsége, hogy pontosan négy dobozban van a feliratnak megfelelő fogkrém, megegyezik annak a valószínűségével,
hogy a Blend-a-med Soda Bicarbonate nincs a helyén, ez pedig
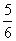 .
.

15. A virágoskertben tavasszal háromféle tulipán (piros, sárga, rózsaszín) és kétféle nárcisz (fehér és sárga) nyílik egyszerre. A szobában a váza mellett egy kosárkában mindig van öt cédula, a következő feliratokkal: piros tulipán, sárga tulipán, rózsaszín tulipán, fehér nárcisz, sárga nárcisz. Mama minden nap egy cédula kihúzásával dönti el, melyikből szedjen a vázába. Mekkora a valószínűsége annak, hogy április 20-án és 21-én is
- sárga nárciszt;
- ugyanolyan virágot;
- tulipánt szed?
Megoldás:
- Mama első nap öt cédulából húz, a sárga nárcisz valószínűsége
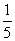 .
Másnap szintén öt cédulából húz, a sárga nárcisz valószínűsége ismét
.
Másnap szintén öt cédulából húz, a sárga nárcisz valószínűsége ismét 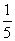 .
Így két egymást követő napon a sárga nárcisz valószínűsége:
.
Így két egymást követő napon a sárga nárcisz valószínűsége: 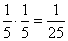 .
.
- Ha a két napon ugyanolyan virágot szed, akkor a második napi húzásnál ugyanazt a cédulát kell kihúzni, amit első
nap. Egy adott cédula kihúzásának a valószínűsége
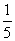 . Tehát annak a
valószínűsége, hogy két egymást követő napon ugyanolyan virágot szed mama a vázába
. Tehát annak a
valószínűsége, hogy két egymást követő napon ugyanolyan virágot szed mama a vázába 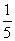 .
.
- Az ötféle virágból három tulipán, így annak a valószínűsége, hogy mama tulipános cédulát húz
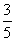 .
A második napon is ugyanazokból a cédulákból húz, így két egymást követő napon a tulipán valószínűsége:
.
A második napon is ugyanazokból a cédulákból húz, így két egymást követő napon a tulipán valószínűsége:
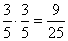 .
.
