A KöMaL 2011. áprilisi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2011. május 10-én LEJÁRT. |
M. 314. Mérjük meg, hogyan változik a tűzhelyre feltett fazék víz hőmérséklete az idő függvényében,
a) ha fedő van a fazékon;
b) ha nincs fedő a fazékon!
Közli: Homoki-Nagy Olga, Monor
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2011. május 10-én LEJÁRT. |
P. 4337. A ,,Felfedezések és találmányok atlasza'' szerint a viking hajók nagyjából 24 m hosszúak és 5,2 m szélesek voltak, 1,8 m merüléssel.
Becsüljük meg a hajók teherbírását, ha a teljes terhelésnél a merülésük 10%-kal nőtt meg.
Közli: Vladár Károly, Budapest
(3 pont)
P. 4338. Hogyan határozhatjuk meg szerkesztéssel egy trapéz alakú lemez súlypontjának (tömegközéppontjának) helyét?
Faragó Andor (1877--1944) feladata nyomán
(4 pont)
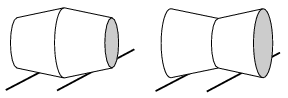
P. 4339. Egyforma gumidugókat az ábrán látható módon összeragasztottunk. A testeket a vízszinteshez képest enyhén döntött, az eredeti dugók magasságával megegyező nyomtávú sínpárra helyezzük, és hagyjuk, hogy legördüljenek. Meglepve tapasztaljuk, hogy az egyik test minden próbálkozás során eléri a lejtő alját, a másik viszont a sokadik kísérlet után is ,,kisiklik''. Melyik? (A testek mindvégig tisztán gördülnek.)
Közli: Vigh Máté, Pécs
(4 pont)
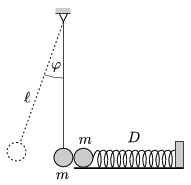
P. 4340. Egy  =1 m hosszú fonálon függő kisméretű, m=0,4 kg tömegű golyó érintkezik a vízszintes síkon nyugvó, ugyancsak m tömegű, azonos sugarú golyóval, amely egy D=10 N/m direkciós erejű csavarrugó egyik végéhez van erősítve az ábra szerint. A rugó kezdetben nyújtatlan, és másik vége ki van támasztva. A fonálingát
=1 m hosszú fonálon függő kisméretű, m=0,4 kg tömegű golyó érintkezik a vízszintes síkon nyugvó, ugyancsak m tömegű, azonos sugarú golyóval, amely egy D=10 N/m direkciós erejű csavarrugó egyik végéhez van erősítve az ábra szerint. A rugó kezdetben nyújtatlan, és másik vége ki van támasztva. A fonálingát  =20o-kal kitérítjük, majd kezdősebesség nélkül elengedjük.
=20o-kal kitérítjük, majd kezdősebesség nélkül elengedjük.
a) Mekkora sebességgel ütközik a két golyó? Adjuk meg, hogy hány százalékos hibát követünk el, ha a fonálinga lengésidő-képletéből kiindulva számítjuk a leérkezés sebességét!
b) Mennyi idő múlva kerül az inga ismét maximális kitérésű helyzetbe, miután a másik golyóval abszolút rugalmasan, centrálisan ütközött? (Minden súrlódás elhanyagolható.)
Közli: Holics László, Budapest
(5 pont)
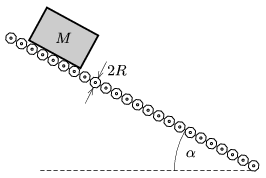
P. 4341. Egy hosszú,  hajlásszögű lejtő rögzített tengelyű, könnyen forgó, tömör gumihengerekből áll. Az m tömegű, R sugarú görgők szorosan egymás mellett helyezkednek el, de össze nem érnek. Legfeljebb mekkora sebességre gyorsulhat fel a lejtő tetejére helyezett M tömegű láda? (A súrlódási együttható a láda és a görgők között elég nagy.)
hajlásszögű lejtő rögzített tengelyű, könnyen forgó, tömör gumihengerekből áll. Az m tömegű, R sugarú görgők szorosan egymás mellett helyezkednek el, de össze nem érnek. Legfeljebb mekkora sebességre gyorsulhat fel a lejtő tetejére helyezett M tömegű láda? (A súrlódási együttható a láda és a görgők között elég nagy.)
Amerikai versenyfeladat
(5 pont)
P. 4342. Három virágváza áll az asztalon, egyik se magasabb 40 cm-nél. Mindegyik belseje függőleges henger. Az elsőbe 2 deci, a másodikba 3 deci, a harmadikba 6 decinél is több víz fér. Az első henger keresztmetszetének területe 10 cm2, a két másiké 20-20 cm2. Mindegyik vázában ugyanannyi víz van.
Megfigyelhetjük, hogy egy bizonyos hangvilla hangja mindig felerősödik, ha azt közvetlenül valamelyik váza fölé, a váza ,,szájához'' helyezzük. Mindegyik váza alja 1 cm vastag, a hang terjedési sebessége levegőben 340 m/s, a hangvilla rezgésszáma pedig kisebb 1 kHz-nél.
a) Mennyi víz van a vázákban?
b) Mennyi a hangvilla rezgésszáma?
c) Milyen magas a harmadik váza?
Közli: Radnai Gyula, Budapest
(5 pont)
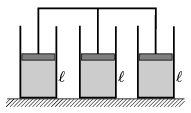
P. 4343. Az ábrán látható három henger azonos keresztmetszetű. A hengerekben azonos anyagi minőségű, ideálisnak tekinthető gáz van, melyet a külső levegőtől azonos súlyú, könnyen mozgó dugattyú zár el. A dugattyúk mereven egymáshoz vannak kapcsolva. Kezdetben a gázok sűrűsége, t=27 oC-os hőmérséklete és a gázoszlopok  =20 cm-es magassága azonos.
=20 cm-es magassága azonos.
Mennyivel emelkednek a dugattyúk, ha a középső tartályban lévő gáz hőmérsékletét t'=117 oC-ra emeljük, miközben a két szélső tartályban a gázok hőmérsékletét állandó értéken tartjuk?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4344. 4,5 V-os zsebtelepre sorbakapcsolunk egy kondenzátort és egy nagy ellenállást, amelyen keresztül lassan töltődik fel a kondenzátor. A bekapcsolás után 1 perccel a kondenzátoron mérhető feszültség 3 V.
Mekkora lesz a kondenzátor feszültsége
a) 2 perc múlva;
b) 3 perc múlva?
Varga István (1952--2007) feladata
(4 pont)
P. 4345. Egy 30 cm hosszú kartoncső egyik végére 2 dioptriás, 8 cm átmérőjű gyűjtőlencsét, másik végére egy ugyancsak 8 cm átmérőjű, -5 dioptriás szórólencsét ragasztunk. A csövet a gyüjtőlencsés végével a Nap felé fordítjuk, és a szórólencsétől 10 cm, majd 20 cm távolságra helyezünk el egy ernyőt.
Mit látunk az ernyőn?
Mátrai Tibor fizikaverseny, Eger
(4 pont)
P. 4346. 100 éve, 1911-ben megjelent cikkében Rutherford úgy gondolkodott, hogy egy, az aranyatom középpontja felé haladó  -részecskének a sebessége az atom középpontjától olyan távolságban csökken le nullára, ahol a kezdeti mozgási energiája egyenlő lesz a rá vonatkozó elektromos potenciális energiával. Az elektromos potenciál egyrészt az atom közepén elhelyezkedő pozitív töltéstől, másrészt az atomot egyenletesen megtöltő negatív töltéstől származik. Az aranyatom sugarát vegyük 10-10 m-nek.
-részecskének a sebessége az atom középpontjától olyan távolságban csökken le nullára, ahol a kezdeti mozgási energiája egyenlő lesz a rá vonatkozó elektromos potenciális energiával. Az elektromos potenciál egyrészt az atom közepén elhelyezkedő pozitív töltéstől, másrészt az atomot egyenletesen megtöltő negatív töltéstől származik. Az aranyatom sugarát vegyük 10-10 m-nek.
Mekkora a kérdéses távolság, ha az  -részecske sebessége 2.107 m/s?
-részecske sebessége 2.107 m/s?
Közli: Simon Péter, Pécs
(5 pont)
P. 4347. Mekkora energiájú  -foton képes egy ,,álló'' elektronnak ütközve pozitront kelteni? Az elektron (és a pozitron) nyugalmi energiája 510 keV.
-foton képes egy ,,álló'' elektronnak ütközve pozitront kelteni? Az elektron (és a pozitron) nyugalmi energiája 510 keV.
Közli: Gnädig Péter, Vácduka
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

