A KöMaL 2014. februári informatika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

I-jelű feladatok

A beküldési határidő 2014. március 10-én LEJÁRT.

I. 340. Egy baráti társaság egy hétvégi délutánon hálózati csevegést folytatott zárt körben. A chatszoba 13:00 órakor történő megnyitása után a beszélgetések párban történtek, de egy-egy tag egyszerre több beszélgetésben is részt vehetett.

A csevegő programban előre tárolták a társaság névsorát, majd minden beszélgetésről a kezdeményező és partnerének a nevét, a beszélgetés kezdő és befejező időpontját a chatszoba megnyitása után. Rendelkezésünkre állnak és a honlapunkról letölthetők a csevegő program által rögzített adatok a cseveges.txt állományban.

Az állomány első sorában a baráti társaság tagjainak száma N található (2 $\le$ N $\le$ 20), majd N sorban a tagok névsora (a nevek szóközt nem tartalmaznak). A rákövetkező sorban a beszélgetések száma: M (2 $\le$ M $\le$ 1000), majd azt ezt követő M sorban két szám (BE, BV) és két név (B1, B2) található. Az első szám - BE (0 $\le$ BE $\le$ 720) - a beszélgetés kezdő időpontja a chatszoba megnyitása után és a második szám - BV (BE $\le$ BV $\le$ 720) - a befejezés időpontja, mind a kettő percben. Az első név (B1) a beszélgetés kezdeményezője, a második név (B2) a beszélgetőtárs neve.

Például:

Készítsünk programot i340 néven, amely megoldja az alábbi feladatokat.

A képernyőre írást igénylő részfeladatok eredményének megjelenítése előtt írjuk a képernyőre a feladat sorszámát (például 3. feladat: ). A beolvasás előtt a várt tartalomra vonatkozó üzenetet jelenítsünk meg (például: Add meg a beszélgetők nevét!). Az ékezet nélküli kiírás is megengedett.

1. Olvassuk be és tároljuk el a cseveges.txt állomány adatait a későbbi feladatok megoldásához szükséges formában.

2. Írjuk ki a képernyőre a beszélgetések átlagos idejét két tizedes jegy pontosan.

3. Kérjük be a felhasználótól a baráti társaság egyik tagjának a nevét és írjuk a beszélgetéseinek teljes idejét.

4. Számoljuk meg, hogy hányszor fordult az elő, hogy a beszélgetés befejezése után a kezdeményező újra ugyanazt a barátját hívja beszélgetésre anélkül, hogy mást hívott volna.

5. Gyűjtsük ki és írjuk a képernyőre azoknak a nevét, akik nem beszélgettek senkivel.

6. Írjuk ki annak a leghosszabb időszakasznak elejét és végét, amikor nem beszélgetett senki.

7. Adjuk meg, hogy a chatszoba nyitása után óránként hány különböző tag vett részt a beszélgetésekben. (Egy beszélgetés több óra adataihoz is tartozhat.)

8. Határozzuk meg azt az időpontot, amikor legtöbb ember vett részt a beszélgetésekben. Ha több ilyen van, akkor elegendő egyet.

9. Adjuk meg az egymással legtöbb időt beszélgető tagok nevét.

Beküldendő a program forráskódja (i340.pas, i340.cpp, ...), valamint a program rövid dokumentációja (i340.txt, i340.pdf, ...), amely megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.

Letölthető fájl: cseveges.txt

(10 pont)

megoldás, statisztika

I. 341. Minden nagyobb városban kiterjedt tömegközlekedési hálózat üzemel. Sok helyen nagyobb forgalmú vonalakat elektromos üzeművé alakították környezetvédelmi okokból. A kötött pályás közlekedés az előnyök mellett bizonyos hátrányokat is hordoz, például egy meghibásodott villamos megbénítja a forgalmat, egyik jármű nem előzheti meg a másikat.

Feladatunk a villamosvonal járatainak szimulációs modellezése.

Mivel jelentős forgalmi és utaslétszámbeli változások fordulhatnak elő még egy napon belül is, ezért csak egy, viszonylag homogénnek tekinthető időszakot vizsgálunk a modellel.

A vizsgálathoz a közlekedési vállalattól megkaptunk néhány adatot, amelyek a megallo.txt fájlban, megállónként megtalálhatók:

$\bullet$ az egyes megállók milyen időbeli távolságra vannak egymástól, ha a forgalom nem akadályozza a haladást $(t_{\rm{meg\'all\'o}})$ ;

$\bullet$ az elmúlt év során a vizsgált időszakban forgalmi okokból (közlekedési lámpa, többi közlekedő) legfeljebb mennyivel vett több időt igénybe két megálló közötti szakasz (t_plusz);

$\bullet$ az adott megállóba percenként átlagosan hány felszálló érkezik (fel);

$\bullet$ az adott megállóban a jármű utasainak hány százaléka száll le (le_sz).

A fentiek mellett ismerjük az első járat indulási idejét (például 8:00), a követési időt (például 0:10), valamint azt, hogy egy utas fel- vagy leszállásához mennyi idő szükséges (például 0:00:01). Az itt nem említett, járatok menetidejét befolyásoló tényezőket elhanyagoljuk.

Készítsünk táblázatot az alábbi módon öt egymást követő járat vizsgálatához:

$\bullet$ a munkafüzet megálló munkalapján helyezzük el a megallo.txt fájlban található adatokat;

$\bullet$ a teszt munkalapon járatonként - és megállónként - számítsuk ki a következő adatokat: érkezési idő, leszálló utasok száma, felszálló utasok száma, a le- és felszálláshoz szükséges idő, indulási idő;

o a felszállók számát az első járat esetén a követési idő, a további járatoknál az előző járat érkezése óta eltelt idő alapján határozzuk meg;

o a megállók közötti plusz idő 0 és a megadott idő között véletlenszerűen bármennyi lehet;

o a le- és felszállók száma a megadott értéktől véletlenszerűen, legföljebb 20 százalékkal eltérhet (a törtszámú utassal számolás megengedett);

o ügyeljünk arra, hogy egy járat se előzhesse meg a másikat (azonos érkezési idő);

$\bullet$ készüljön diagram, amelyről leolvasható, hogy az egyes járatok közötti követési idő hogyan alakult az egyes megállókban az induláskori követési időhöz képest;

$\bullet$ ügyeljünk arra, hogy a megoldás az indulási és a követési idő, az utascserélési sebesség, valamint a megállók jellemzőinek módosítását kövesse.

A táblázat elkészítését követően próbáljuk meg kideríteni, hogy mely paraméter(ek) módosítására érzékeny leginkább a rendszer.

Beküldendő a megoldást tartalmazó táblázat (i341.xls, i341.ods, ...) és a rövid dokumentációja (i341.txt, i341.pdf, ...), amely a paraméterek módosításával kapcsolatos leírást tartalmazza, valamint azt, hogy a táblázat mely táblázatkezelő mely verziójával készült.

Letölthető fájl: megallo.txt

(10 pont)

megoldás, statisztika

I. 342. A ChronoZoom nevű (http://www.chronozoom.com) nemzetközi projekt az ,,idő dinamikus atlasza'' tömör funkció-leírást kapta. A HTML5 nyelvre építkező kezelőfelület grafikusan jeleníti meg az időszakaszokat. Az idővonal egyes pontjaihoz gyűjteményeket: képeket, videókat és cikkeket lehet rendelni. A megjelenítés érdekessége, hogy az idővonal dinamikusan zoomolható, ezért különböző léptékű időszakaszokat tekinthetünk át. Az idővonalak további idővonalakat tartalmazhatnak tetszőleges mélységben.

Készítsünk saját idővonalat valamelyik, a KöMaL profiljához illeszkedő tudományág történetének bemutatására. A munkánk tartalmazzon több rész-idővonalat, akkor is, ha azok nem feltétlenül lesznek gyűjteményekkel feltöltve. Az elkészített gyűjteményekben több dokumentum szerepeljen, és lehetőleg adjuk meg ezek forrását is, akár elektronikusak, akár papíralapúak.

A szerkesztés alapjainak elsajátításához ajánljuk a videómegosztó portálokon található oktatóvideókat. A tartalom előállításához pedig a tudománytörténeti könyveket, például Simonyi Károlynak A fizika kultúrtörténete című munkáját.

Beküldendő egy dokumentum (i342.txt, i342.pdf, ...), amely tartalmazza a tudománytörténet tartalmának és időpontjaihoz felhasznált forrást, valamint az elkészített idővonalra mutató hivatkozást.

(10 pont)

megoldás, statisztika

S-jelű feladatok

A beküldési határidő 2014. március 10-én LEJÁRT.

S. 87. Az Újító Matematikusok Közössége egy új definíciót alkotott. Ezentúl egy természetes számokból álló véges sorozat Újított Legnagyobb Közös Osztóját, röviden ÚLNKO-ját a következőképpen határozzák meg: veszik a sorozat elemszámát, és megszorozzák a sorozat elemeinek régi, elavult típusú legnagyobb közös osztójával. Ez a szám lesz a sorozat ÚLNKO-ja. Rögtön kaptunk tőlük egy feladatot: adott egy (a₁,...,a_N) pozitív egészekből álló sorozat ( $1 \le N \le 100\;000$ ). Adjuk meg az összes összefüggő (szomszédos elemekből álló) részsorozat ÚLNKO-jának maximumát.

A program olvassa be a standard input első sorából N-et, majd a következő sorból az a_i számokat (1 $\le$ a_i $\le$ 10¹¹). Írja a standard output első és egyetlen sorába azt a legnagyobb elérhető pozitív egészet, melyet egy összefüggő részsorozat ÚLNKO-jaként kapunk.

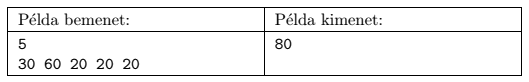
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül. Részpontszámok kaphatóak, ha a program N $\le$ 200-ra megoldást ad, illetve ha N $\le$ 5000-re megoldást ad.

Beküldendő egy tömörített s87.zip állományban a program forráskódja (s87.pas, s87.cpp, ...) az .exe és más, a fordító által generált állományok nélkül, valamint a program rövid dokumentációja (s87.txt, s87.pdf, ...), amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.

(10 pont)

megoldás, statisztika

Figyelem!

Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

Már regisztráltál?
Új vendég vagy?