A KöMaL 2016. márciusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2016. április 11-én LEJÁRT. |
I. 397. (É.) Egy 32 sakkozó között zajló versenyt a következők szerint rendeztek meg a szervezők. Az első fordulóban csoportokat hoztak létre, majd a csoportokon belül körmérkőzéseket játszottak egymással a játékosok. A versenyzőknek kezdetben 100 pontjuk volt. A játszmák győztese minden mérkőzés után megkapta az ellenfél pontjainak 20-ad részét, és pontszámát fölfelé egészre kerekítették. A vesztes pontjai nem változtak. Döntetlen eredmény esetén a játszmát újra kellett játszani.
Az első forduló után kialakult pontszámok és a magyar versenyzők nevei megtalálhatók a sakk.txt, honlapunkról letölthető szöveges állományban. A fájl minden sora egy versenyző adatait tartalmazza, a pontszám, a vezeték és a keresztnév vagy keresztnevek egymástól egy-egy szóközzel vannak elválasztva. A fájl csak ékezetek nélküli karaktereket tartalmaz, nincsenek benne fölösleges sorok vagy szóközök, a versenyzők neve előtt nincs előtag (pl. Dr. vagy ifj.). Egy rövid részlet a fájlból:
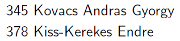
A második fordulóban egyenes kieséssel folytatták a versenyt a játékosok. A sakkozókat pontszám szerint csökkenő sorrendbe állították, és sorrendben az első játékos játszott a legutolsóval, a második az utolsó előttivel, és így tovább. Az azonos pontszámú versenyzőket nevük szerint ABC rendbe sorolták be. Az első körben az így kialakított párosok egy játszmát játszottak egymással. A győztesek a fentiek alapján növelték pontjaikat, a vesztesek kiestek a további játékból. Ezután ismét elvégezték a sorba rendezést, és a második körben a még játékban lévő játékosok játszottak egymással az előbbi módon. Minden további körben ugyanígy történt a párosok kiválasztása és a pontok számítása, egészen a döntő játszmáig.
Készítsünk programot i397 néven, amely megoldja a következő feladatokat. Az egyes feladatok megoldása előtt írjuk ki a feladat sorszámát a képernyőre, pl. ,,3. feladat:''. A nevek kiírásakor minden feladatban a keresztnevek helyett csak azok első betűjét és egy pontot jelenítsünk meg, figyelve a magyar nyelvben használt kettős betűkre.
1. Olvassuk be a sakk.txt állományt, és tároljuk el az adatokat.
2. Írjuk ki a képernyőre a versenyzők adatait a beolvasás szerinti sorrendben a következő formában:
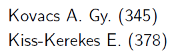
3. A második fordulóban a párosok közötti játszmákat szimuláljuk úgy, hogy a játékosnak az aktuális pontszámával arányos esélye legyen a győzelemre. Legyen az egyik versenyző jelenlegi pontja \(\displaystyle A\), a másik versenyzőé \(\displaystyle B\). Generáljunk egy véletlen egész számot 1 és \(\displaystyle A+B\) között. Az első versenyző a győztes, ha a véletlenszám 1 és \(\displaystyle A\) közötti, és a másik versenyző a győztes, ha \(\displaystyle A+1\) és \(\displaystyle A+B\) közötti. Készítsünk ElsoNyer néven logikai értéket visszaadó függvényt, amelynek két egész paramétere két játékos pontszáma. A függvény szimulálja a játszmát véletlenszám generálásával, majd adjon vissza igaz értéket, ha az első játékos nyert, és hamis értéket, ha a második.
4. Játsszuk le a második forduló első körét az előbb elkészített függvény segítségével. Írjuk a képernyőre a sakkozók kör végén érvényes adatait. Egy-egy sorban az egymás ellen játszók szerepeljenek a 2. feladat szerinti formában, három vonallal (---) elválasztva.
5. Adjuk meg, hogy melyik versenyző és ki ellen szerezte a legtöbb pontot a második forduló első körében. A választ foglaljuk mondatba, pl. ,,Kiss-Kerekes E. (396) szerezte a legtöbb pontot (18) Kovacs A. Gy. (345) ellen''.
6. Játsszuk végig a második forduló második körét is, és írjuk ki a kor2.txt állományba a kör nyolc játszmája után érvényes eredményeket és a párosítást a 4. feladatban leírtaknak megfelelően.
7. Soroljuk föl azokat a második körben kiesett sakkozókat, akik több pontot szereztek, mint a legkisebb pontszámot szerző továbbjutó, és írjuk a képernyőre nevük rövidített alakját egymástól vesszővel elválasztva.
8. Játsszuk végig a további köröket is, és írjuk a képernyőre a döntőben részt vevő két sakkozó adatait az utolsó kör előtt, illetve a kör után.
Beküldendő egy tömörített i397.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
A megoldáshoz fölhasználható bemeneti állomány: sakk.txt.
(10 pont)
I. 398. Egy bankfiók előterében készpénz felvételére és befizetésére alkalmas automatákat helyeztek el. Ebbe a helyiségbe a bank nyitvatartási idején kívül az ügyfél bankkártyájának leolvasása után lehet belépni, illetve onnan távozni. Biztonsági okokból naplóállományba kerül az ajtó nyitása és a bankautomatán végzett tranzakció néhány adata. Honlapunkról letölthető az egyik nap nyitvatartás utáni adatait tartalmazó naplo.txt fájl (tabulátorokkal tagolt, UTF-8 kódolású szövegállomány).
Nyissuk meg táblázatkezelő program segítségével a naplo.txt fájlt úgy, hogy az első beolvasott adat az A1-es cellába kerüljön. A táblát mentsük a táblázatkezelő saját formátumában i398 néven.
A naplóban feljegyzésre került minden esemény ideje (óra, perc), az esemény jellege, az öt jegyű kártyaszám és pénzműveletkor az összeg. Az esemény 1, ha belépés, \(\displaystyle -1\), ha távozás, 2, ha pénzbefizetés és \(\displaystyle -2\), ha pénzfelvétel történt.
Példa:
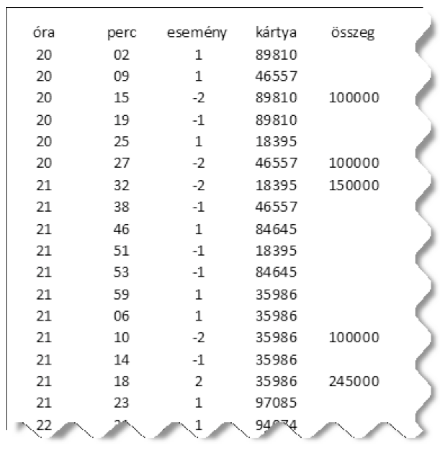
Oldjuk meg a következő feladatokat képletek, függvények és hivatkozások segítségével. Az események számát nem lehet előre tudni, ezért 150 lehetséges eseményre készítsük fel a megoldásunkat.
A megoldás során tetszőleges számú oszlopban végezhetünk segédszámításokat, amelyeket lássunk el magyarázó szöveggel. A kérdésekre adott válaszokat egy összegzést tartalmazó munkalapon jelenítsük meg.
- Mennyit fizettek be és mennyit vettek fel összesen a naplóállományban található adatok alapján?
- Melyik bankkártyával vették fel a legtöbb pénzt? (Ha több ilyen volt, akkor időben az elsőt adjuk meg.)
- Hányan voltak a legtöbben egyszerre a bankfiók előterében? Ez mikor fordult elő legelőször?
- Hány különböző kártyával történt tranzakció?
- Hány olyan kártya volt, amellyel befizetés és pénzfelvétel is történt?
- Ábrázoljuk külön munkalapon, oszlopdiagram segítségével, hogy 20:00 és 8:00 óra között óránként hány pénzügyi tranzakció történt. A diagramot lássuk el feliratokkal és formázzuk úgy, hogy kifejező legyen.
Beküldendő egy tömörített állományban (i398.zip) a táblázatkezelő munkafüzet, illetve egy rövid dokumentáció, amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója.
A megoldáshoz letölthető fájl: naplo.txt.
(10 pont)
I. 399. Az első táblázatkezelő programot, a VisiCalc-ot, 1979-ben Dan Bricklin és Bob Frankston készítette. Bár a program fejlesztése 1985-ben befejeződött, a mindössze kb. 28 KB méretű, karakteres felületre tervezett alkalmazás az interneten ma is elérhető (http://www.bricklin.com/history/vcexecutable.htm). A program a 32 bites Windows 7 felületén segédeszköz nélkül, más operációs rendszerek (pl. Windows 10) esetén pedig megfelelő segédprogrammal, pl. a DosBox-szal futtatható. Az internetről a VisiCalc használati útmutatóját is letölthetjük (http://toastytech.com/manuals/VisiCalc%201.1.pdf).
Ebben a feladatban egy kis Közért (korabeli élelmiszerbolt) délelőtti forgalmát kell feldolgozni az 1979-es év első feléből. Az A és B oszlopokban az értékesítés sorrendjében rögzítették az eladott termék kódját, valamint az abból eladott mennyiséget. Az egyes termékek kódját, nevét és egységárát az F2:H8 tartomány tartalmazza. (Az adatok 1979 első feléből származnak.)
1. Nyissuk meg VisiCalc segítségével a visi.vc fájlt, és oldjuk meg az alábbi feladatokat. A kész táblázatot noszt.vc néven mentsük.
2. Függvény segítségével határozzuk meg a C2 cellában, hogy mennyi az A2 cellában lévő termék egységára.
3. Képlet segítségével számoljuk ki a D2 cellában az A2 cellában lévő termék B2 cellában lévő mennyisége után fizetendő összeget.
4. Másoljuk át a C2 és D2 cellákban lévő képletet az alattuk lévő cellákba az 50. sorig.
5. Határozzuk meg az I2:I8 tartományban az egyes termékekből eladott mennyiségeket. Segédoszlopokat az L oszloptól jobbra vehetünk fel.
6. Határozzuk meg az egyes termékekből származó bevételt a J2:J8 tartományban.
7. Töltsük ki szaggatott vízszintes vonallal az F9:J9 tartományt.
8. Határozzuk meg képlet segítségével a G10:G13 tartományban az árusított termékek számát, illetve a termékekből származó átlagos bevételt, összes bevételt, illetve legnagyobb bevételt.
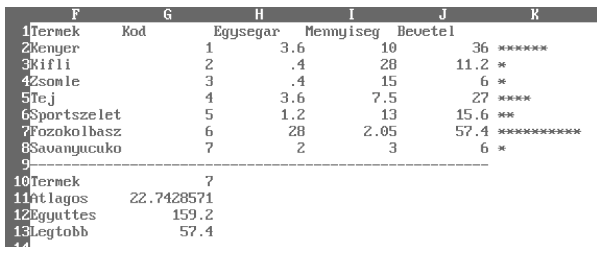
9. Állítsuk a cellák szélességét 11 karakteresre.
10. Szemléltessük a K oszlopban az egyes termékekből származó bevételek arányát ,,\(\displaystyle \mathtt{*}\)'' karakterek segítségével úgy, hogy a legtöbb bevételt 10 db ,,\(\displaystyle \mathtt{*}\)'' jelképezze.
Beküldendő egy tömörített állományban (i399.zip) a noszt.vc fájl.
A megoldásoz letölthető állományok: visi.vc, VC.COM
(10 pont)
 |
I/S-jelű feladatokA beküldési határidő 2016. április 11-én LEJÁRT. |
I/S. 7. Adott egy \(\displaystyle 5\times 5\)-ös táblázat. Minden mezőjén vagy van csoki, vagy nincs. Összesen \(\displaystyle 0\le K\le 22\), páros számú mező üres, a többi mezőn van csoki. A bal felső \(\displaystyle (1;1)\) koordinátájú, és a jobb alsó \(\displaystyle (5;5)\) koordinátájú mezőn biztosan van csoki. Két gyerek szeretne csokit enni. Az egyik a bal felső, a másik a jobb alsó sarokból indul. Először megeszik az ott található csokoládét, majd egyszerre egy lépést tesznek egy élszomszédos mezőre, amely csokit tartalmaz. Ezután megeszik az itt található csokit, és ismét egyszerre lépnek az előbbi szabály szerint. Céljuk az, hogy az összes csokit összeszedve találkozzanak, és az utolsó csokit közösen egyék meg. Korábban tilos találkozniuk, csak a csokiszedés legvégén. Hányféleképp járhatják be a táblázatot, ha egy mezőre nem léphetnek többször (hiszen ott már nincs csoki)?
A program olvassa be a standard input első sorából \(\displaystyle K\)-t, majd a következő \(\displaystyle K\) sorból az egyes csokit nem tartalmazó mezők koordinátáit, és írja a standard output első és egyetlen sorába a lehetséges bejárások számát, vagy 0-t, ha nincs bejárás. Két bejárás különböző, ha van olyan gyerek, aki máshogyan lépett.
|
Magyarázat: A középső sorból négy csoki hiányzik. Ebben a sorban az 5. helyen kell találkozniuk. Könnyen látható, hogy mindkettőjük lépéssorozata egyértelmű.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített is7.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2016. április 11-én LEJÁRT. |
S. 106. Adott egy ország \(\displaystyle N\) (\(\displaystyle 1\le N\le 17\)) várossal. A városok közül \(\displaystyle M\) db kétirányú úttal van összekötve. Szeretnénk az országban minél több típusú tudományos konferenciát szervezni. Egy adott típusú konferenciát több városban is meg lehet szervezni, de egy városban legfeljebb egy konferencia szervezhető. Egy adott városból csak szomszédos városba lehet menni konferenciára, illetve természetesen az adott városban szervezett konferencia is látogatható. Szeretnénk minél több konferenciatípust szervezni, úgy, hogy bármely város lakói bármelyik típusú konferenciára elmehessenek. Például egyféle konferenciát mindig tudunk szervezni: minden városban ugyanazt a típust szervezzük meg.
A program olvassa be a standard input első sorából \(\displaystyle N\)-et és \(\displaystyle M\)-et, majd a következő \(\displaystyle M\) sorból az egyes utakat összekötő városokat, és írja a standard output első és egyetlen sorába, a lehető legtöbb típusú konferenciák számát, amit az adott ország meg tud szervezni.
|
Magyarázat: Az 1-es és 4-es városokban \(\displaystyle A\) típusú, a 2-es és 3-as városokban \(\displaystyle B\) típusú konferenciát szervezünk.
Pontozás és korlátok: A programhoz mellékelt, a helyes megoldás elvét tömören, de érthetően leíró dokumentáció 1 pontot ér. A programra akkor kapható meg a további 9 pont, ha bármilyen hibátlan bemenetet képes megoldani az 1 mp futásidőkorláton belül.
Beküldendő egy tömörített s106.zip állományban a program forráskódja, valamint a program rövid dokumentációja, amely a fentieken túl megadja, hogy a forrás mely fejlesztői környezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

