A KöMaL 2018. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2018. március 12-én LEJÁRT. |
K. 577. Xavér kivett három lapot egy csomag francia kártyából, és letette őket egymás mellé az asztalra. A letett lapokról az alábbi információkat árulta el:
– A három lap között van egy király, amelyiktől közvetlenül jobbra 1 vagy 2 dáma található.
– A három lap között van egy dáma, amelyiktől közvetlenül balra 1 vagy 2 dáma található.
– A három lap között van egy kőr, amelyiktől közvetlenül balra 1 vagy 2 pikk található.
– A három lap között van egy pikk, amelyiktől közvetlenül jobbra 1 vagy 2 pikk található.
Balról jobbra haladva milyen lapok lehetnek az asztalon?
(6 pont)
K. 578. Egy \(\displaystyle 2 \times n\)-es táblázat felső sorába beírjuk a pozitív egész számokat 1-től \(\displaystyle n\)-ig növekvő sorrendben, az alsó sorába pedig csökkenő sorrendben. Hány olyan 50-nél kisebb \(\displaystyle n\) pozitív egész szám van, melyre minden felső sorban lévő szám és az alatta lévő szám relatív prím?
(6 pont)
K. 579. 105 lányt és 95 fiút tetszőlegesen 100 párba osztunk. A fiú párok kezet fognak, a lány párok pacsiznak, a vegyes párok pedig elkezdenek táncolni. Mutassuk meg, hogy 5-tel kevesebb kézfogás történik, mint pacsi.
(6 pont)
K. 580. Mely derékszögű háromszögekre igaz, hogy \(\displaystyle x > 2(z -y)\), feltéve, hogy \(\displaystyle z > y \ge x\)?
(6 pont)
K. 581. Adjuk meg az összes ABBA alakú négyjegyű négyzetszámot.
(6 pont)
K. 582. Milyen hosszú lehet az a szó, amelynek betűi pontosan 180-féleképpen rendezhetők sorba? Keressünk ilyen értelmes magyar szót.
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2018. március 12-én LEJÁRT. |
C. 1462. Egy számtani sorozat első tagja \(\displaystyle a_1=3\), differenciája 9. Bizonyítsuk be, hogy a sorozat tagjai között minden természetes \(\displaystyle k\) szám esetén szerepel \(\displaystyle 3\cdot 4^k\).
(5 pont)
C. 1463. A szabályos \(\displaystyle ABC\) háromszög belsejében található \(\displaystyle M\) pontból az \(\displaystyle AB\), \(\displaystyle BC\) és \(\displaystyle CA\) oldalakra állított merőlegesek talppontja rendre \(\displaystyle H\), \(\displaystyle K\) és \(\displaystyle P\). Bizonyítsuk be, hogy
\(\displaystyle (i)\) \(\displaystyle {|AH|}^2+{|BK|}^2+{|CP|}^2= {|HB|}^2+{|KC|}^2+{|PA|}^2\);
\(\displaystyle (ii)\) \(\displaystyle |AH|+|BK|+|CP|= |HB|+|KC|+|PA|\).
Mathematical Competitions in Croatia
(5 pont)
C. 1464. Azt mondjuk, hogy egy tetszőleges \(\displaystyle A\) természetes számból a nála kisebb \(\displaystyle B\) természetes szám kiolvasható, ha \(\displaystyle A\) számjegyei közül néhányat letörölve, majd a megmaradó jegyeket a sorrend megváltoztatása nélkül összeolvasva megkapjuk \(\displaystyle B\)-t. Melyik a legkisebb olyan természetes szám, melyből bármely háromjegyű szám kiolvasható?
(5 pont)
C. 1465. A \(\displaystyle PQR\) szabályos háromszög és a \(\displaystyle QRST\) négyzet csúcsain áthaladó \(\displaystyle PS\) és \(\displaystyle RT\) egyenesek metszéspontja legyen \(\displaystyle M\). Igazoljuk, hogy a \(\displaystyle PTM\) háromszög egyenlőszárú.
(5 pont)
C. 1466. Egy bizottság az év folyamán tizenkét alkalommal ülésezett. A tagok közül minden ülésen 10-en vettek részt, és bármelyik két tag legfeljebb egyszer volt együtt jelen. Legalább hány tagból áll a bizottság?
(5 pont)
C. 1467. Az \(\displaystyle O\) középpontú, \(\displaystyle 2r\) sugarú és az \(\displaystyle O\)-n áthaladó, \(\displaystyle r+1\) sugarú körök metszéspontjai legyenek \(\displaystyle A\) és \(\displaystyle B\). Mekkora lehet \(\displaystyle r\), ha az \(\displaystyle AB\) szakasz a kisebbik kör átmérője?
(5 pont)
C. 1468. Igazoljuk, hogy ha \(\displaystyle a\) és \(\displaystyle b\) nemnegatív számok, akkor
\(\displaystyle \frac12 {(a+b)}^2+\frac14(a+b)\ge a\sqrt b+b\sqrt a\,. \)
Mikor áll fenn egyenlőség?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2018. március 12-én LEJÁRT. |
B. 4930. Bergengóciában, ,,Turágus'' faluban három vallás képviselői a Napimádók, a Holdimádók és a Földimádók. A vallási előírások szerint a szentélynek a falu valamennyi házától vett távolságösszege a lehető legkisebb kell, hogy legyen (függetlenül attól, hogy a házban milyen vallás hívei élnek.) Igazoljuk, hogy ha a Napimádóknak, és a Holdimádóknak már van egy-egy szentélye a faluban, akkor a Földimádók is tudnak építeni egy újabb szentélyt. (A falu sík terepen terül el, és a szentély, illetve a falu házai is pontszerűnek tekintendőek.)
(3 pont)
B. 4931. Mutassuk meg, hogy egy háromszög \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\) oldalaira teljesül, hogy
\(\displaystyle \frac{a^2(b+c)+b^2(a+c)}{abc}>3. \)
(3 pont)
B. 4932. A Nagy Meseországi Bestiáriumban az év minden hetére jut egy-egy sárkány. A legfiatalabb sárkány, Alajos 13-fejű, a következő sárkány Botond 14-fejű ... (és így tovább, minden újabb idősebb sárkánynak eggyel több feje van, mint az előzőnek), míg a legidősebb sárkány Zoárd 64-fejű. A meseországi szerzetesek elkészítették a Nagy Sárkánymesés Kódexet. A Kódexbe csak az a mese kerülhet be, amelyben szereplő sárkányok fejeinek a száma pontosan 1001. Bármely két mese esetén van legalább egy olyan sárkány, ami csak az egyik mesében szerepel. Miután a Kódexbe a fenti feltételeknek megfelelő összes lehetséges mesét lejegyezték, a 13-fejű Alajos, vagy a 14-fejű Botond szerepel-e több mesében?
(5 pont)
B. 4933. Határozzuk meg az egységnégyzetbe írt maximális kerületű szabályos háromszög területét.
(4 pont)
B. 4934. Tetszőleges \(\displaystyle n\) és \(\displaystyle k\) pozitív egészek esetén jelölje \(\displaystyle f(n,k)\) azt, hogy egy \(\displaystyle n \times k\)-as rácstéglalap egyik átlója hány egységnégyzet belsején halad keresztül. Hány olyan \(\displaystyle n,k\) számpár van, amelyre \(\displaystyle n\ge k\), és \(\displaystyle f(n,k)=2018\)?
(4 pont)
B. 4935. Adott az \(\displaystyle O\) csúcsú szög szárai közé írt két érintő kör, \(\displaystyle \omega_1\) és \(\displaystyle \omega_2\). Egy, az \(\displaystyle O\) pontból induló félegyenes az \(\displaystyle \omega_1\) kört az \(\displaystyle A_1\) és a \(\displaystyle B_1\), az \(\displaystyle \omega_2\) kört az \(\displaystyle A_2\) és a \(\displaystyle B_2\) pontban metszi úgy, hogy \(\displaystyle OA_1<OB_1<OA_2<OB_2\) (lásd az ábrát). A \(\displaystyle \gamma_1\) kör belülről érinti az \(\displaystyle \omega_1\) kört és érinti az \(\displaystyle \omega_2\) kör \(\displaystyle A_1\) ponton átmenő érintőit. A \(\displaystyle \gamma_2\) kör pedig belülről érinti az \(\displaystyle \omega_2\) kört és érinti az \(\displaystyle \omega_1\) kör \(\displaystyle B_2\) ponton átmenő érintőit. Bizonyítsuk be, hogy a \(\displaystyle \gamma_1\) és \(\displaystyle \gamma_2\) körök sugara egyenlő.
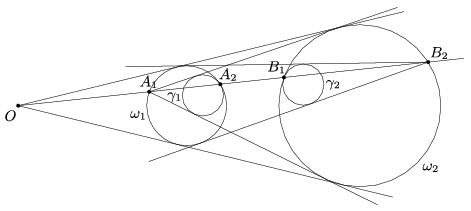
(Kvant)
(5 pont)
B. 4936. Rögzítsük a \(\displaystyle k\) körben az átmérőtől különböző \(\displaystyle AB\) húrt, ennek felezőpontja legyen \(\displaystyle F\). A \(\displaystyle k\) körvonal \(\displaystyle A\)-tól és \(\displaystyle B\)-től különböző pontja legyen \(\displaystyle P\). A \(\displaystyle PF\) egyenes messe a \(\displaystyle k\) kört másodszor \(\displaystyle X\)-ben, \(\displaystyle X\) tükörképe az \(\displaystyle AB\) felezőmerőlegesére \(\displaystyle Y\). Bizonyítsuk be, hogy van a síknak egy olyan pontja, amelyen a \(\displaystyle PY\) egyenes \(\displaystyle P\) minden helyzetében átmegy.
Javasolta: Surányi László (Budapest)
(5 pont)
B. 4937. A síkon kiválasztunk rácsnégyszögeket úgy, hogy igaz rájuk a következő: akárhogy színezzük a rácspontokat véges sok színnel, mindig van olyan kiválasztott négyszög, amelynek minden csúcsa ugyanolyan színű. Bizonyítsuk be, hogy van végtelen sok olyan kiválasztott négyszög, amelyek közül semelyik kettőnek nincs közös csúcsa.
Javasolta: Surányi László (Budapest)
(6 pont)
B. 4938. Ismert, hogy a tórusz felületére rá lehet rajzolni a \(\displaystyle 7\) pontú teljes gráfot (lásd pl. a Császár-poliédert). Egy sárga görbe bögre oldalán kijelölünk 7 pontot, és bármelyik kettőt össze akarjuk kötni egy-egy görbével úgy, hogy semelyik két görbének ne legyen közös belső pontja. Legalább hány görbét kell ennek eléréséhez átvezetnünk a görbe bögre fülén?
(6 pont)
 |
A-jelű feladatokA beküldési határidő 2018. március 12-én LEJÁRT. |
A. 716. Az \(\displaystyle ABC\) háromszög belsejében, az \(\displaystyle A\)-ból induló szögfelezőn felvettünk egy \(\displaystyle D\) pontot. Legyen a \(\displaystyle BD\) és \(\displaystyle AC\) egyenesek metszéspontja \(\displaystyle E\), a \(\displaystyle CD\) és \(\displaystyle AB\) metszéspontja \(\displaystyle F\). Az \(\displaystyle ABC\) háromszög körülírt körét az \(\displaystyle EF\) egyenes a \(\displaystyle P\) és \(\displaystyle Q\) pontokban metszi. Mutassuk meg, hogy ha \(\displaystyle O\) a \(\displaystyle DPQ\) kör középpontja, akkor \(\displaystyle OD\) merőleges \(\displaystyle BC\)-re.
Javasolta: Michael Ren (Andover, Massachusetts, USA)
(5 pont)
A. 717. Egy pozitív egészt lustának nevezünk, ha nincs \(\displaystyle 3\)-nál nagyobb prímosztója. Mutassuk meg, hogy két szomszédos négyzetszám között legfeljebb két lusta szám lehet.
Javasolta: Gyenes Zoltán és Kós Géza (Budapest)
(5 pont)
A. 718. Jelölje \(\displaystyle \mathbb{R}[x,y]\) a kétváltozós, valós együtthatós polinomok halmazát. Azt mondjuk, hogy az \(\displaystyle f\in\mathbb{R}[x,y]\) polinomnak az \(\displaystyle (a,b)\) számpár zérushelye, ha \(\displaystyle f(a,b)=0\).
Igaz-e, hogy ha a \(\displaystyle p,q\in\mathbb{R}[x,y]\) polinomoknak végtelen sok közös zérushelye van, akkor létezik olyan nem konstans \(\displaystyle r\in\mathbb{R}[x,y]\) polinom, ami kiemelhető \(\displaystyle p\)-ből és \(\displaystyle q\)-ból is?
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

