A KöMaL 2009. szeptemberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2009. október 12-én LEJÁRT. |
M. 298. Mérjük meg, hogy mennyi idő alatt olvad meg egy csapvízből készült jégkocka szobahőmérsékletű csapvízben, és ugyanakkora mennyiségű, ugyanakkora hőmérsékletű sós vízben.
Ismételjük meg a mérést úgy is, hogy a jégkockákba befagyasztunk elég nagy nehezéket ahhoz, hogy lemerüljenek a csapvíz, illetve a sós víz aljára.
(Érdemes ételfestékkel színezni a jégkockákat.)
Közli: Honyek Gyula, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2009. október 12-én LEJÁRT. |
P. 4174. Ha két füzetet egymással szembefordítunk, és lapjaikat egymás közé lapozzuk, majd a füzeteket két ujjunkkal összeszorítjuk, akkor egy felnőtt sem képes széthúzni azokat. Mi a jelenség magyarázata?
Jedlik Ányos verseny, Nyíregyháza
(3 pont)
P. 4175. Van-e az ábrán látható áramkörben megjelölt \(\displaystyle A\), \(\displaystyle B\), \(\displaystyle C\), \(\displaystyle D\) pontok között azonos potenciálú? Melyik két pont között van a legnagyobb feszültség?
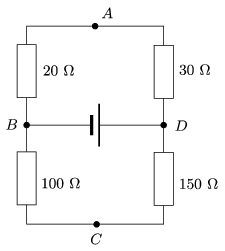
Nagy László verseny, Kazincbarcika
(3 pont)
P. 4176. Egy gyerek szánkón csúszik lefelé a \(\displaystyle 10^\circ\)-os lejtőn. Van egy kis hátszél, amely 10,5 N nagyságú, a mozgás irányába mutató erővel írható le. A gyerek és a szánkó együttes tömege 65 kg, a szánkó és a hó között a súrlódási együttható 0,15.
\(\displaystyle a)\) Nyugalomból indulva mekkora sebességgel ér le a szánkó a 125 m hosszú lejtő aljára?
\(\displaystyle b)\) Mennyi idő szükséges ehhez?
Tornyai Sándor verseny, Hódmezővásárhely
(4 pont)
P. 4177. Az \(\displaystyle m=0{,}5\) kg tömegű, \(\displaystyle \ell=80\) cm hosszúságú homogén rudat két fonállal függesztjük fel. Mekkora lesz a rúd \(\displaystyle A\) pontjának gyorsulása, valamint a bal oldali fonalat feszítő erő közvetlenül a jobb oldali fonál elvágása után?
Cornides István verseny, Révkomárom (Szlovákia)
(4 pont)
P. 4178. Szódavizes pohárba 1,2 g/cm\(\displaystyle {}^3\) sűrűségű, 2 cm\(\displaystyle {}^3\) térfogatú csokoládédarab esett. A csokoládéra szén-dioxid-buborékok kezdenek tapadni. Legalább mennyi a buborékok össztérfogata, amikor a csokoládédarab elkezd emelkedni?
Tarján Imre verseny, Szolnok
(4 pont)
P. 4179. Határozzuk meg a 20 g héliumból és 8 g hidrogénből álló gázkeverék állandó nyomáson illetve állandó térfogaton vett fajhőinek hányadosát.
Budó Ágoston verseny, Szeged
(4 pont)
P. 4180. Az ábrán látható vízszintes asztallapon álló \(\displaystyle m\) tömegű, \(\displaystyle Q\) töltésű anyagi pontot függőleges \(\displaystyle v_{0}\) kezdősebességgel felfelé indítjuk. Az indítási helytől mekkora távolságra és mekkora sebességgel esik vissza az asztalra, ha \(\displaystyle E\) nagyságú, vízszintes irányú elektromos tér is hat rá?
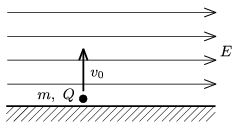
Bay Zoltán verseny, Sarkad
(4 pont)
P. 4181. Az ábrán látható \(\displaystyle B=0{,}167\) T indukciójú homogén mágneses mező szélessége \(\displaystyle \ell=5\) cm. Az erővonalakra merőlegesen egy proton lép be, amely a mezőn való áthaladása után \(\displaystyle \varphi=30^\circ\)-os szögben térül el.
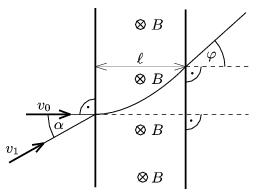
\(\displaystyle a)\) Határozzuk meg a proton \(\displaystyle v_{0}\) sebességét, illetve a mezőn való áthaladás időtartamát.
\(\displaystyle b)\) Mekkora ellenfeszültséggel lehet a protont \(\displaystyle s=10\) cm úton lefékezni, és mennyi a fékezési idő?
\(\displaystyle c)\) Tegyük fel, hogy \(\displaystyle v_{1}=2\cdot 10^6\) m/s sebességgel az ábrán látható \(\displaystyle \alpha\) szög alatt egy másik proton is érkezik. Legalább mekkora az \(\displaystyle \alpha\) szög, ha ez a részecske visszaverődik a mágneses falon?
Vermes Miklós verseny, Sopron
(5 pont)
P. 4182. Egy pontszerűnek tekinthető, 5 W sugárzási teljesítményű fénycső 425 nm hullámhosszúságú monokromatikus fényt sugároz. A fényforrástól 1 m távolságban a fénysugarakra merőlegesen egy fotocella katódja van elhelyezve, melynek sugara 0,5 cm, anyagának kilépési munkája \(\displaystyle 2\cdot 10^{-19}\) J. A fotocella katódja és anódja közé egy 2 nF kapacitású kondenzátort kapcsolunk.
\(\displaystyle a)\) Mennyi a sugárzás egy fotonjának az energiája, és hány foton érkezik másodpercenként a katódra?
\(\displaystyle b)\) Mekkora maximális sebességgel hagyják el a az elektronok a katódot?
\(\displaystyle c)\) Mekkora feszültségre töltődik fel a kondenzátor?
Wigner Jenő verseny, Békéscsaba
(5 pont)
P. 4183. Mióta bomlik a 214-es tömegszámú radioaktív ólomizotóp, ha a felezési ideje 26,8 perc, és az atomok eredeti számának már csak 1 ezreléke van meg?
Lánczos Kornél verseny, Székesfehérvár
(4 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

