A KöMaL 2016. októberi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2016. november 10-én LEJÁRT. |
M. 362. Vágjunk le 2 cm széles papírcsíkokat különböző fajtájú papírokból! Mérjük meg ezek lehajlását a vízszintesen befogott papírcsík szabad hosszának függvényében! Ugyanabból a papírból más-más helyről kivágott papírcsíkok ugyanúgy hajlanak le?
Közli: Márki-Zay János, Hódmezővásárhely
(6 pont)
 |
G-jelű feladatokA beküldési határidő 2016. november 10-én LEJÁRT. |
G. 581. Hol és hogyan történhet meg, hogy a Napot nem keleten, hanem nyugaton látjuk felkelni?
(3 pont)
G. 582. Egy alumíniumhasáb élei \(\displaystyle a=20\) cm, \(\displaystyle b=30\) cm, \(\displaystyle c=40\) cm hosszúak. Az alumínium sűrűsége \(\displaystyle \varrho=2700~\rm kg/m^3\). Mekkora nyomást fejthet ki a vízszintes talajra állított alumíniumhasáb?
(3 pont)
G. 583. Egy 500 W teljesítményű merülőforralóval 10 percen át melegítettünk 2 liter térfogatú, kezdetben \(\displaystyle 20~{}^\circ\)C hőmérsékletű vizet. A víz hőmérséklete ennek következtében \(\displaystyle 45~{}^\circ\)C-ra nőtt. Mekkora volt a melegítés hatásfoka?
(3 pont)
 |
P-jelű feladatokA beküldési határidő 2016. november 10-én LEJÁRT. |
P. 4864. Egy testet ugyanakkora kezdősebességgel két különböző szög alatt hajíthatunk el, hogy ugyanolyan messzire jusson. Mekkora ezen két szög, ha a mozgás ideje – elhanyagolva a közegellenállást – \(\displaystyle n\)-szer akkora az egyik, mint a másik esetben?
Strasser V. Benő (1884–1966) feladata
(4 pont)
P. 4865. Két, egymásra merőleges, egyenes országúton egyenletes sebességgel halad két gépkocsi az ábra szerint. Kezdetben a járművek \(\displaystyle x_0=6\) km és \(\displaystyle y_0=3\) km távolságra voltak a kereszteződéstől. Az \(\displaystyle AO\) pályán haladó jármű sebessége \(\displaystyle v_1=36\) km/h. Mozgásuk során innen 9 perc alatt kerülnek egymáshoz legközelebbi helyzetbe.
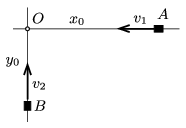
Mekkora a \(\displaystyle BO\) egyenesen haladó jármű sebessége, és mekkora a járművek között mérhető legkisebb távolság?
Közli: Holics László, Budapest
(5 pont)
P. 4866. Két, egyenként \(\displaystyle \ell\) hosszúságú fonálinga függ egymás mellett úgy, hogy a fonalak végén lévő golyók az ábrán látható módon összeérnek. Az egyik golyó \(\displaystyle M\) tömege sokkal nagyobb a másik golyó \(\displaystyle m\) tömegénél.
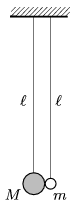
\(\displaystyle a)\) Kissé kitérítjük a bal oldali ingát úgy, hogy a \(\displaystyle M\) tömegű golyó emelkedése \(\displaystyle h\ll \ell\) legyen, azután elengedjük. A két golyó rugalmas ütközése után legfeljebb milyen magasra emelkedhet fel a \(\displaystyle m\) tömegű golyó?
\(\displaystyle b)\) Ha mindkét ingát kitérítjük ellentétes irányban úgy, hogy mindkét golyó emelkedési magassága \(\displaystyle h\ll \ell\) legyen, akkor a rugalmas ütközés után milyen maximális magasságba emelkedik fel a \(\displaystyle m\) tömegű golyó?
Közli: Lambodara Mishra, Ahmedabad, India
(4 pont)
P. 4867. Két, azonos irányban haladó test tökéletesen rugalmatlanul ütközik. Az egyik test tömege a másik test tömegének \(\displaystyle n\)-szerese, sebessége pedig a másik sebességének \(\displaystyle n\)-ed része (\(\displaystyle n\ge2\), egész). Mekkora \(\displaystyle n\) esetén vész el az összes mozgási energiának legalább a fele?
Közli: Tornyos Tivadar Eörs, Budapest
(4 pont)
P. 4868. \(\displaystyle N\) molekulából álló ideális gáz valamely egyensúlyi folyamatának egyenlete:
\(\displaystyle \frac{p}{p_0}+\frac{V}{V_0}=1. \)
Legfeljebb mekkora lehet e folyamat során a gáz hőmérséklete?
Közli: Radnai Gyula, Budapest
(4 pont)
P. 4869. Egy \(\displaystyle \ell\) hosszúságú (húzó-nyomó) rugót \(\displaystyle F_1\) erővel \(\displaystyle d<\ell/2\) hosszúságúra nyomunk össze. Ezután a rugót félbevágjuk, és a két egyforma darabot egymás mellett, egyszerre (,,párhuzamosan'') ismét \(\displaystyle d\) hosszúságúra nyomjuk össze. Mekkora \(\displaystyle F_2\) erő kell ehhez?
Hány egyforma darabra kell vágnunk egy \(\displaystyle \ell=10\,d\) hosszú rugót, hogy az az \(\displaystyle F_n\) erő, amivel a darabokat párhuzamosan \(\displaystyle d\) hosszúságúra összenyomhatjuk, a lehető legnagyobb legyen? Mekkora ez az erő?
Közli: Woynarovich Ferenc, Budapest
(5 pont)
P. 4870. A világűr egy távoli részén, egymástól távol lévő, azonos méretű két ólomgolyó között ugyanakkora elektrosztatikus vonzóerő hat, mint amekkora a közöttük fellépő gravitációs vonzóerő. A potenciálkülönbség a két golyó között 5 kV. Mekkorák a golyók, ha az össztöltésük zérus?
Közli: Vass Miklós, Budapest
(4 pont)
P. 4871. A papír síkjára merőleges, \(\displaystyle B\) indukciójú, homogén mágneses mezőbe \(\displaystyle v\) sebességgel lövünk be egy \(\displaystyle m\) tömegű, \(\displaystyle q\) töltésű részecskét. A részecske a mágneses mezőbe való belépés előtt a mező (ábra szerinti alsó) szélével párhuzamosan, attól \(\displaystyle d\) távolságra halad. A mezőn való áthaladás közben a haladás iránya \(\displaystyle \varphi=60^\circ\)-kal változik.

\(\displaystyle a)\) Milyen előjelű a részecske töltése, ha a mágneses indukcióvektor az ábrán ,,befelé'' mutat?
\(\displaystyle b)\) Mekkora a részecske sebessége?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4872. Adjunk becslést, hogy mennyi idő alatt nyel el a déli napsütésben egy Balaton-parti strandoló a napsugárzásból annyi energiát, amennyi gamma-sugárzás esetén halálos egésztest-dózist (6 Gy) jelentene.
Szilárd Leó verseny feladata nyomán
(4 pont)
P. 4873. Egy kerékpár generátorára (amelyet sokszor tévesen ,,dinamónak'' neveznek) egy állandó értékű ohmos ellenállást kapcsoltunk. Megmértük, hogy a generátor állandó \(\displaystyle n\), illetve \(\displaystyle 2n\) fordulatszámmal való forgatásához átlagosan \(\displaystyle M_1\), illetve \(\displaystyle 1{,}8\,M_1\) forgatónyomaték szükséges. Mekkora forgatónyomatékot kell kifejtenünk \(\displaystyle 3n\) fordulatszám mellett? A generátor mechanikai veszteségei elhanyagolhatók. (Lásd még a témával kapcsolatos cikket a 435. oldalon.)
Közli: Bilicz Sándor, Budapest
(6 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

