Az A. 850. feladat (2023. március)

A. 850. Igazoljuk, hogy létezik egy olyan \(\displaystyle N\) pozitív valós szám, melyre tetszőleges \(\displaystyle a,b>N\) valós számok esetén az \(\displaystyle a\) és \(\displaystyle b\) hosszúságú oldalakkal rendelkező téglalap kerülete lefedhető egymásba nem nyúló egység sugarú körlapokkal (a körlapok érinthetik egymást).

Javasolta: Váli Benedek (Budapest)

(7 pont)

A beküldési határidő 2023. április 11-én LEJÁRT.

Első megoldás:

Válasszuk úgy \(\displaystyle N\)-t, hogy ha \(\displaystyle a>N\), akkor \(\displaystyle \frac{a}{a+4} \geq \sqrt{1-1/100}\). Ezt meg tudjuk tenni, mivel ahogy \(\displaystyle a \to \infty\) úgy \(\displaystyle \frac{a}{a+4} \to 1\). Ez elsőre elég véletlenszerűnek tűnhet, de majd kiderül a megoldásból, hogy miért így választottuk \(\displaystyle N\)-t.

Legyenek tehát \(\displaystyle a,b>N\) valós számok, és legyenek a téglalap csúcsai a \(\displaystyle (0,0)\), \(\displaystyle (a,0)\), \(\displaystyle (a,b)\), \(\displaystyle (0,b)\) pontok. A terv az, hogy olyan egység sugarú körökkel fedjük a kerületet, melyek között szerepel négy kör, melyek középpontjai \(\displaystyle (u,v)\), \(\displaystyle (a+u,v)\), \(\displaystyle (a+u, b+v)\), \(\displaystyle (u, b+v)\) valamilyen \(\displaystyle u,v \leq \frac{1}{10}\) számok esetén, ahol az \(\displaystyle u\) és \(\displaystyle v\) értékét később határozzuk meg. Gondoljuk meg, hogy ha például az \(\displaystyle (u,v)\) középpontú kört már leraktuk, akkor onnantól a többi körnek meg tudjuk határozni a középpontját, melyeknek ebben a fedésben kell lenni (egyedül a téglalap csúcsainak közelében lehetnének komplikációk, de ott megadtuk, hogy mik lesznek a fedésben lévő körök középpontjai). Az \(\displaystyle (u,v)\) középpontú körlap fedi a \(\displaystyle (0,0)\) csúcsot és körülötte egy darabot a kerületből, az \(\displaystyle x\) tengelyre eső oldalt az \(\displaystyle (u+\sqrt{1-v^2},0)\) pontban metszi. Egy körnek muszáj fednie az \(\displaystyle (u+\sqrt{1-v^2}+\varepsilon,0)\) pontot tetszőlegesen kis \(\displaystyle \varepsilon\) esetén, ami csak úgy lehetséges, hogy van egy másik kör is, ami áthalad az \(\displaystyle (u+\sqrt{1-v^2},0)\) ponton, így a feladat feltételei szerint ebben a pontban a két körnek érintnie kell egymást, azaz a másik kör középpontjának az \(\displaystyle (u+2\sqrt{1-v^2},-v)\) pontban kell lenni. Ehhez hasonlóan látható, hogy ez a kör az \(\displaystyle x\) tengelyt másodszor az \(\displaystyle (u+3\sqrt{1-v^2},0)\) pontban metszi, így kell lennie egy következő körnek, ami itt érinti ezt, azaz a középpontja az \(\displaystyle (u+4\sqrt{1-v^2},v)\) pontban lesz. Így folytatva látható, hogy minden \(\displaystyle (u+4k\sqrt{1-v^2},v)\) és \(\displaystyle (u+(4k+2)\sqrt{1-v^2},-v)\) pontban lesz egy középpont, ahol \(\displaystyle k\) egész szám, és nem túl nagy, azaz amíg nem érjük el a téglalap jobb oldalát.

Ahhoz, hogy az \(\displaystyle (a+u,v)\) egy kör középpontja tudjon lenni, az kéne, hogy valamelyik középpont legyen a fent felsoroltak közül, azaz \(\displaystyle (u+4k\sqrt{1-v^2},v)\) alakban írható valamilyen \(\displaystyle k\) pozitív egész számra. Ha ez teljesül, akkor ezzel a körrel bezárólag a felvett körlapok teljesen lefedik a téglalap alsó oldalát. Továbbá ez akkor teljesül, ha \(\displaystyle a=4k\sqrt{1-v^2}\). Legyen \(\displaystyle k=\left\lceil \frac{a}{4} \right\rceil\). Ekkor ebből ki tudjuk fejezni \(\displaystyle v\)-t:

\(\displaystyle \sqrt{1-v^2}=\frac{a}{4k} \geq \frac{a}{a+4} \geq \sqrt{1-1/100},\)

\(\displaystyle \frac{a}{4k} \leq 1\) és \(\displaystyle \sqrt{1-v^2}\) folytonos, 0-ban 1-t vesz fel és monoton csökken \(\displaystyle [0,1]\)-n, így a fenti egyenlőtlenségek alapján egyértelműen létezik egy \(\displaystyle v \in \left[0,\frac{1}{10}\right]\) mely kielégíti az egyenletet.

Hasonlóan csináljuk meg ezt a jobb oldalra, itt azt kapjuk, hogy a körök középpontjai \(\displaystyle (a+u,v+4k\sqrt{1-u^2})\) és \(\displaystyle (a-u, (4k+2)\sqrt{1-u^2})\) alakúak, ahol \(\displaystyle k\) egész. Most azt szeretnénk, hogy az \(\displaystyle (a+u,b+v)\) ilyen alakú legyen, azaz \(\displaystyle b+v=v+4k\sqrt{1-u^2}\) legyen valamilyen \(\displaystyle k\) egészre. A fenti gondolatmenethez hasonlóan létezik megfelelő \(\displaystyle u \leq \frac{1}{10}\) és \(\displaystyle k\) egész szám, melyekre teljesül az egyenlet. Látható, hogy ha ennek megfelelően megválasztjuk az \(\displaystyle u\)-t és a \(\displaystyle v\)-t, akkor a fenti gondolatmenethez hasonlóan meghatározva a körök középpontjait, a felső és a bal oldala a téglalapnak is fedhető körökkel, ráadásul az \(\displaystyle (u,b+v)\) éppen egy kör középpontja lesz. Tehát az egyetlen dolog, amit meg kell még gondolni, hogy a körök nem metszenek egymásba. Világos, hogy csak a csúcsok környékén lehetne probléma, és ott is csak úgy, hogy ha a csúcsot fedő kör két szomszédja összeérne, de az \(\displaystyle u,v \leq \frac{1}{10}\) választás miatt ha \(\displaystyle O_1\), \(\displaystyle O_2\) és \(\displaystyle O_3\) három szomszédos kör középpontja ilyen sorrendben, akkor \(\displaystyle O_1O_2O_3 \sphericalangle \geq 60^{\circ}\), ami éppen azt jelenti, hogy az \(\displaystyle O_1\) és \(\displaystyle O_3\) középpontú körök nem metszenek egymásba.

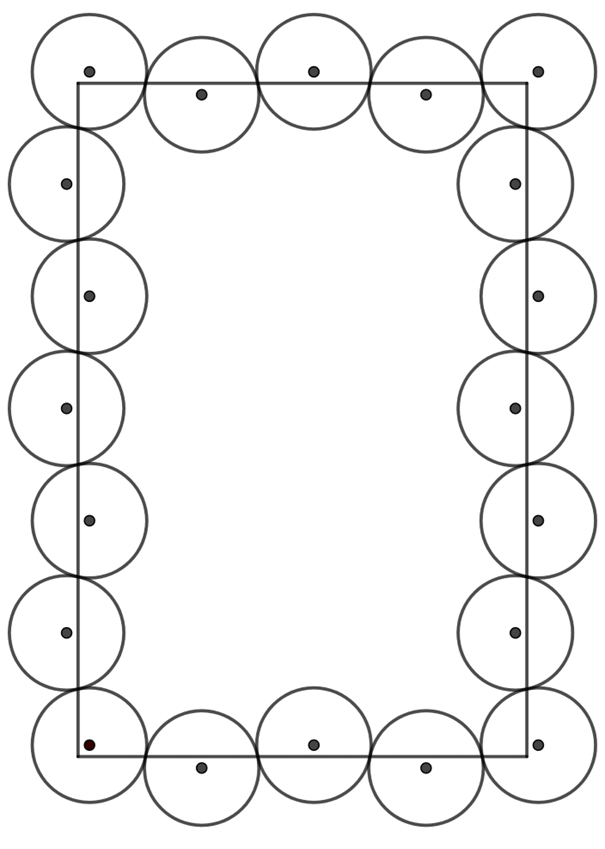
Második megoldás:

Az előző megoldáshoz nagyon hasonló az alap gondolat, csak most azt szeretnénk, ha az \(\displaystyle (u,v)\), \(\displaystyle (a-u,v)\), \(\displaystyle (a-u, b-v)\), \(\displaystyle (u, b-v)\) pontok lennének a fedésben lévő körök középpontjai valamilyen \(\displaystyle \frac{1}{20} \leq u,v \leq \frac{1}{10}\) számok esetén. Az előző megoldáshoz hasonlóan, az \(\displaystyle (u,v)\) középpontú körből kiindulva, az alsó oldalt fedve \(\displaystyle (u+4k\sqrt{1-v^2},v)\) és \(\displaystyle (u+(4k+2)\sqrt{1-v^2},-v)\) alakúak lesznek a körök középpontjai, és azt szeretnénk, hogy \(\displaystyle (a-u,v)\) ilyen alakú legyen, azaz \(\displaystyle a-u=u+4k\sqrt{1-v^2}\) teljeüljön valamilyen \(\displaystyle k\) egész esetén. Máshogy mondva azt szeretnénk, hogy az \(\displaystyle \frac{a-2u}{4\sqrt{1-v^2}}\) szám egész legyen. Ehhez hasonlóan a jobb oldalt fedve azt a feltételt kapjuk, hogy \(\displaystyle \frac{b-2v}{4\sqrt{1-u^2}}\) egész legyen, és az előző megoldáshoz hasonlóan ekkor a felső és bal oldalt is le tudjuk fedni a feltételeknek megfelelően, és a körök nem metszenek egymásba, ha \(\displaystyle u, v \leq \frac{1}{10}\).

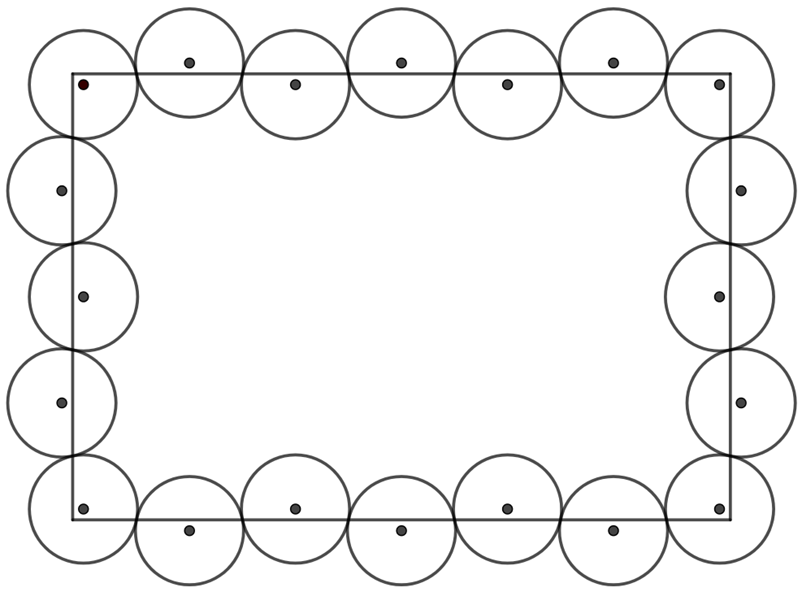
Tehát visszavezettük a feladatot arra, hogy kéne találni \(\displaystyle \frac{1}{20} \leq u,v \leq \frac{1}{10}\) számokat, melyekre \(\displaystyle \frac{a-2u}{4\sqrt{1-v^2}}\) és \(\displaystyle \frac{b-2v}{4\sqrt{1-u^2}}\) egyszerre egész számok. Tekintsük az \(\displaystyle f, g \ : \ \left[\frac{1}{20}, \frac{1}{10}\right]^2 \to \mathbb{R}\) függvényeket, melyek a fent leírt módon rendelnek, azaz \(\displaystyle f(u,v)=\frac{a-2u}{4\sqrt{1-v^2}}\) és \(\displaystyle g(u,v)=\frac{b-2v}{4\sqrt{1-u^2}}\). Azt kell igazolni, hogy van olyan érték, amikor mindkét függvény egész számot vesz fel.

Figyeljük meg a következőket a függvényekről. Először is világos, hogy \(\displaystyle f\) és \(\displaystyle g\) folytonos. Másodszor, ha \(\displaystyle a\) és \(\displaystyle b\) elég nagy, akkor ha \(\displaystyle u\)-t egy nagyon kicsit megváltoztatjuk, míg \(\displaystyle v\)-t fixen hagyjuk, akkor \(\displaystyle f\) nagyon kicsit változik, míg \(\displaystyle g\) eléggé megváltozik. Szemléletesen ez világos, most gondoljuk meg precízebben. Azt állítjuk, hogy ha \(\displaystyle (u,v) \in \left[\frac{1}{20}, \frac{1}{10}\right]^2\) és \(\displaystyle \varepsilon>0\) számmal elmozdítjuk \(\displaystyle u\)-t, azaz az \(\displaystyle (u+\varepsilon,v)\) párt tekintjük, ahol \(\displaystyle u+\varepsilon<\frac{1}{10}\) továbbra is teljesül, akkor

\(\displaystyle |f(u,v)-f(u+\varepsilon,v)|\leq \varepsilon \ \ \text{ és } \ \ |g(u,v)-g(u+\varepsilon,v)|\geq 1000\varepsilon.\)

Az első egyenlőtlenség világos, az \(\displaystyle f\) függvényben a nevező legalább kettő, míg a számláló \(\displaystyle -2\varepsilon\)-nal változik meg. A második egyenlőtlenség bizonyítása kicsit bonyolultabb: legyen \(\displaystyle c=\frac{1/20}{\sqrt{1-1/400}}\). Ez éppen a \(\displaystyle h(x)=\sqrt{1-x^2}\) függvény deriváltjának abszolút értéke az \(\displaystyle \frac{1}{20}\) helyen. Figyeljük meg, hogy a \(\displaystyle h(x)\) függvény éppen az origó középpontú egységkör egyenlete, így konkáv az \(\displaystyle \left[\frac{1}{20}, \frac{1}{10}\right]\) intervallumon, tehát a deriváltja monoton csökken, azaz az \(\displaystyle \left[\frac{1}{20}, \frac{1}{10}\right]\) intervallumon \(\displaystyle \frac{1}{20}\)-ban minimális a derivált abszolút értéke, és ott éppen \(\displaystyle c\). Emiatt

\(\displaystyle |h(u)-h(u+\varepsilon)| \geq c\varepsilon,\)

mivel a Lagrange-tétel szerint létezik egy olyan \(\displaystyle t \in (u,u+\varepsilon)\) melyre \(\displaystyle h'(t)=\frac{h(u+\varepsilon)-h(u)}{\varepsilon}\), és tudjuk, hogy \(\displaystyle |h'(t)| \geq c\). A \(\displaystyle |g(u,v)-g(u+\varepsilon,v)|\) kifejezést csökkentjük, ha a közös számlálójukat csükkentjük, és mindkettőnek növeljük a nevezőjét úgy, hogy a nevezőik különbsége ne csökkenjen, azaz

\(\displaystyle |g(u,v)-g(u+\varepsilon,v)| \geq \frac{b-1}{4}-\frac{b-1}{4+c\varepsilon} = \frac{(b-1)(4+c\varepsilon)-4(b-1)}{4(4+c\varepsilon)} \geq \frac{(b-1)c\varepsilon}{20}.\)

Ebből látható, hogy ha \(\displaystyle N=\frac{20000}{c}+1\), és \(\displaystyle b>N\), akkor teljesül a \(\displaystyle g\) megváltozására kívánt egyenlőtlenség.

Hasonlóan ha \(\displaystyle v\)-t változtatjuk meg \(\displaystyle \varepsilon\)-nal, akkor \(\displaystyle f\) legalább \(\displaystyle 1000\varepsilon\)-nal elmozdul, míg \(\displaystyle g\) legfeljebb \(\displaystyle \varepsilon\)-nal. Figyeljük meg még azt is, hogy ha \(\displaystyle u\)-t növeljük, akkor \(\displaystyle f\) csökken és \(\displaystyle g\) nő, míg ha \(\displaystyle v\)-t növeljük, akkor \(\displaystyle f\) nő és \(\displaystyle g\) csökken. Most csináljuk a következőt: induljunk ki az \(\displaystyle (x_0, y_0)=(\frac{1}{15},\frac{1}{15})\) pontból. Haladjunk az \(\displaystyle x\) tengely mentén (azaz növeljük \(\displaystyle u\)-t) addig, amíg \(\displaystyle g\) egész lesz, legyen ez az \(\displaystyle (x_1,y_1)\) pont. A fenti megfigyelések alapján \(\displaystyle y_0=y_1\) és \(\displaystyle |x_1-x_0| \leq \frac{1}{1000}\). Innen növeljük az \(\displaystyle y\) koordinátát, amíg \(\displaystyle f\) egész nem lesz, legyen ez először az \(\displaystyle (x_2, y_2)\) pontban. Ez megint legfeljebb egy \(\displaystyle \frac{1}{1000}\) nagyságú lépés, így ezalatt \(\displaystyle g\) legfeljebb \(\displaystyle \frac{1}{1000}\)-zel csökken. Most megint \(\displaystyle x\)-t növeljük amíg egész nem lesz \(\displaystyle g\), legyen ez az \(\displaystyle (x_3, y_3)\) pontban. Látható, hogy ehhez már legfeljebb \(\displaystyle \frac{1}{1000 \cdot 1000}\)-t kell elmozdulni az \(\displaystyle x\) koordinátával, így \(\displaystyle f\) legfeljebb ennyivel csökken, ráadásul \(\displaystyle g(x_1,y_1)=g(x_3,y_3)\). És így tovább, felváltva növeljük az \(\displaystyle x\) és \(\displaystyle y\) koordinátát, hogy kapjuk az \(\displaystyle (x_n, y_n)\) végtelen pontsorozatot, melyre \(\displaystyle g(x_1,y_1)=g(x_3,y_3)=g(x_5,y_5)= \ldots\) egész és \(\displaystyle f(x_2,y_2)=g(x_4,y_4)=g(x_6,y_6)= \ldots\) is egész. Látható, hogy az \(\displaystyle n.\) lépésben legfeljebb \(\displaystyle \frac{1}{1000^{n-1}}\)-gyel mozdulunk el, így egyrészt, sosem érünk ki az \(\displaystyle \left[\frac{1}{20}, \frac{1}{10}\right]^2\) tartományból, másrészt, a kapott pontsorozat konvergálni fog, és az átviteli elv szerint az \(\displaystyle (x',y')\) határértékre \(\displaystyle g(x',y')=g(x_1,y_1)\) egész és \(\displaystyle f(x',y')=f(x_2,y_2)\) is egész, éppen ahogy akartuk.

Statisztika:

6 dolgozat érkezett.
7 pontot kapott:	Diaconescu Tashi, Lovas Márton, Németh Márton, Varga Boldizsár, Wiener Anna.
0 pontot kapott:	1 versenyző.

A KöMaL 2023. márciusi matematika feladatai