Az A. 901. feladat (2025. február)

A. 901. Tükrözzük a nem egyenlő szárú hegyesszögű $\displaystyle ABC$ háromszöget az Euler-egyenesére, így kapjuk az $\displaystyle A'B'C'$ háromszöget. Az $\displaystyle ABC$ háromszög Feuerbach-körének egy pontja legyen $\displaystyle P$. Minden $\displaystyle X$ pont esetén jelölje $\displaystyle p(X)$ az $\displaystyle X$ pont tükörképét $\displaystyle P$-re.

a) Legyen $\displaystyle e_{AB}$ az az egyenes, amely átmegy az $\displaystyle A$ pont $\displaystyle BB'$ egyenesre vett merőleges vetületén és a $\displaystyle B$ pont $\displaystyle AA'$ egyenesre vett merőleges vetületén. Hasonlóan definiáljuk az $\displaystyle e_{BC}$, $\displaystyle e_{CA}$ egyeneseket. Igazoljuk, hogy ez a három egyenes egy $\displaystyle K$ pontban találkozik.

b) Bizonyítsuk be, hogy két olyan választása is van $\displaystyle P$-nek, amelyre az $\displaystyle Ap(A')$, $\displaystyle Bp(B')$ és $\displaystyle Cp(C')$ egyenesek egy ponton mennek át, továbbá a $\displaystyle {p(A)p(A')\cap BC}$, $\displaystyle {p(B)p(B')\cap CA}$, $\displaystyle {p(C)p(C')\cap AB}$ és $\displaystyle K$ pontok egy egyenesre esnek.

Javasolta: Bán-Szabó Áron (Budapest)

(7 pont)

A beküldési határidő 2025. március 10-én LEJÁRT.

Fel fogunk használni néhány ismertebb, és néhány kevésbé ismert állítást. Ezeket először felsoroljuk, és mutatunk olyan forrást, ahol megtalálható elemi bizonyítás angol nyelven. Minden hivatkozás Roger Johnson: Advanced Euclidean Geometry könyvére vonatkozik.

1. Egy pontnak és az izogonális konjugáltjának a merőleges vetületei a háromszög oldalegyeneseire egy körre esnek.
   Lásd 155. oldal 236. Theorem
2. Az $\displaystyle ABC$ háromszögben a körülírt körön lévő $\displaystyle P$ pont Simson-egyenese merőleges az $\displaystyle AP$ egyenes $\displaystyle A$-izogonális egyenesére.
   Lásd 206. oldal 326. Theorem
3. Egy háromszögben a $\displaystyle P$ pont Simson-egyenese (ahol $\displaystyle P$ a körülírt körnek egy pontja) felezi a magasságpontot és a $\displaystyle P$ pontot összekötő szakaszt. Ebből következik, hogy a $\displaystyle P$ pont Steiner-egyenese, amelyet úgy kapunk, hogy a $\displaystyle P$ pontot tükrözzük a háromszög oldalegyeneseire, átmegy a háromszög magasságpontján.
   Lásd 207. oldal 327. Theorem
4. A körülírt körön átellenes pontok Simson-egyenesei merőlegesek egymásra, és a metszéspontjuk rajta van a Feuerbach-körön.
   Lásd 208. oldal 328. Theorem
5. Adott a síkon négy pont, $\displaystyle A,B,C,D$, melyek közül semelyik három nincs egy egyenesen. Ekkor az $\displaystyle ABC,BCD,CDA,DAB$ háromszögek Feuerbach-körei egy pontban találkoznak, az $\displaystyle ABCD$ pontnégyes Poncelet-pontjában.
   Lásd 242. oldal 396. Theorem
6. Ha a $\displaystyle D$ pontot merőlegesen vetítjük az $\displaystyle ABC$ háromszög oldalegyeneseire, a vetületek körülírt köre átmegy a Poncelet-ponton.
   Lásd 242. oldal 397. Theorem

Vezessünk be néhány pontot. Jelölje $\displaystyle \mathbf{u}$ az Euler-egyenes irányát, $\displaystyle \mathbf{v}$ pedig az erre merőleges irányt. Legyen $\displaystyle V$ a $\displaystyle \mathbf{v}$ irányú ideális pont. A háromszög magasságpontját $\displaystyle H$-val jelöljük. Világos, hogy az $\displaystyle ABC,A'B'C'$ háromszögek körülírt körei és magasságpontjai egybeesnek. Ezen felül még a Feuerbach is közös, ezt $\displaystyle \gamma$-val fogjuk jelölni.

Kezdjük az a)-val. Tekintsük az $\displaystyle ABCV$ pontnégyest. Vegyük észre, hogy bár $\displaystyle V$ a végtelenben van, az $\displaystyle ABCV$ pontnégyesnek lesz Poncelet-pontja. Legyen ugyanis $\displaystyle V_i$ egy $\displaystyle V$-hez tartó pontsorozat. Mivel az $\displaystyle A$, $\displaystyle B$, $\displaystyle C$, $\displaystyle V_i$ pontnégyes Poncelet-pontja rajta van $\displaystyle \gamma$-n, így a Poncelet-pontok sorozata korlátos, tehát van konvergens részsorozata (innentől ezt jelöli $\displaystyle V_i$), és ennek a határértékét tekintjük. Azt állítjuk, hogy ez a pont éppen $\displaystyle K$. Találjuk ki, hogy hova tart az $\displaystyle ABV_i$ Feuerbach-köre, ha $\displaystyle i$ tart a végtelenhez. Tudjuk, hogy a Feuerbach-kör átmegy a magasságvonalak talppontjain, mik lesznek ezek? Az $\displaystyle A$-ból $\displaystyle BV_i$-re állított merőleges talppontja $\displaystyle V$ és $\displaystyle B'$ definíciója szerint éppen $\displaystyle A$ vetületéhez tart a $\displaystyle BB'$ egyenesen, míg a $\displaystyle B$-ből $\displaystyle AV_i$-re állított merőleges talppontja éppen a $\displaystyle B$ vetületéhez tart az $\displaystyle AA'$ egyenesen. Tehát az $\displaystyle ABV_i$ háromszög Feuerbach-köre az $\displaystyle e_{AB}$ egyeneshez tart, hiszen a sugara tart a végtelenhez, ezért átmegy az általunk definiált ponton. Hasonlóan az $\displaystyle e_{BC}$, $\displaystyle e_{CA}$ egyenesek is átmennek ezen.

Vegyük észre, hogy az előző gondolatmenetből az is kiderül, hogy $\displaystyle K\in \gamma$. A b) feladatra rátérve pedig az első jó választása $\displaystyle P$-nek éppen $\displaystyle K$ lesz. Lássuk ezt be. Ehhez először azt igazoljuk, hogy $\displaystyle P=K$ esetében az $\displaystyle Ap(A'),Bp(B'),Cp(C')$ egyenesek az $\displaystyle (ABC)$ körön metszik egymást. Legyen $\displaystyle H$ tükörképe $\displaystyle K$-ra $\displaystyle S$. Ez persze a körön van, mert $\displaystyle \gamma$-nak és az $\displaystyle (ABC)$ körnek $\displaystyle H$ a belső hasonlósági pontja (és a hasonlóság aránya 2). Jelölje $\displaystyle V$ izogonális konjugáltját az $\displaystyle ABC$ háromszögben $\displaystyle V^*$. Mivel $\displaystyle V$ ideális pont, $\displaystyle V^*$ rajta van az $\displaystyle (ABC)$ körön, méghozzá $\displaystyle V^*$ Simson-egyenese $\displaystyle \mathbf{u}$ irányú. Mivel a $\displaystyle V$ ponthoz tartozó talppontok köre ugyanaz, mint a $\displaystyle V^*$ talppontjainak köre (ami ebben az esetben egyenes), azt kaptuk, hogy $\displaystyle V^*$ Simson-egyenese átmegy $\displaystyle K$-n. Ha ezt kétszeresére nagyítjuk $\displaystyle H$-ból, akkor az éppen az $\displaystyle SV^*$ egyenes lesz, ami így tehát $\displaystyle \mathbf{u}$ irányú. Így az $\displaystyle S$ pont tükörképe az Euler-egyenesre – melyet jelöljünk $\displaystyle T$-vel – éppen a $\displaystyle V^*$-gal szemközti pont lesz az $\displaystyle (ABC)$ körön. A tükrözés miatt $\displaystyle T$ Simson-egyenese az $\displaystyle ABC$ háromszögre nézve ugyanaz, mint $\displaystyle S$ Simson-egyenese az $\displaystyle A'B'C'$ háromszögre nézve (hiszen egymás tükörképei, de az irányuk –$\displaystyle \mathbf{v}$ merőleges a tükörtengelyre). És persze a két Simson-egyenes átmegy $\displaystyle K$-n. Most igazoljuk, hogy $\displaystyle S$-ből a $\displaystyle B'C'$-re állított merőleges átmegy $\displaystyle A$-n. Ez a merőleges messe a körülírt kört $\displaystyle S'\neq S$-ben, azt kell belátni, hogy $\displaystyle S'=A$. Jelölje $\displaystyle H'$ a $\displaystyle H$ tükörképét a $\displaystyle B'C'$ egyenesre, ami persze rajta van az $\displaystyle (ABC)$ körön. Mivel $\displaystyle A'H'\parallel S'S$, az $\displaystyle A'H'SS'$ húrtrapéz. A $\displaystyle H'S$ egyenes $\displaystyle B'C'$-re vett tükörképe éppen az $\displaystyle S$ Steiner-egyenese az $\displaystyle A'B'C'$ háromszögre nézve, amiről már tudjuk, hogy $\displaystyle \mathbf{v}$ irányú. Így mivel $\displaystyle AA'$ is $\displaystyle \mathbf{v}$ irányú, $\displaystyle A=S'$. Végül $\displaystyle K$ felezi a $\displaystyle HS$ szakaszt, ezért $\displaystyle p(A')$ rajta lesz az $\displaystyle AS$ egyenesen. Tehát beláttuk, hogy az $\displaystyle Ap(A'),Bp(B'),Cp(C')$ egyenesek $\displaystyle S$-ben találkoznak.

Most belátjuk, hogy a $\displaystyle K$ pontból a $\displaystyle V^*K$ egyenesre állított merőleges átmegy a $\displaystyle p(A)p(A')\cap BC$ ponton (persze akkor a $\displaystyle p(B)p(B')\cap CA$ és $\displaystyle p(C)p(C')\cap AB$ pontokon is). Belátjuk tehát, hogy a $\displaystyle p(A)p(A')\cap BC=Z$ jelöléssel $\displaystyle ZK\perp ZV^*$. Jelölje $\displaystyle W$ a $\displaystyle V^*$ pont merőleges vetületét a $\displaystyle BC$ egyenesen. Messe a $\displaystyle (V^*KW)$ kör a $\displaystyle BC$ egyenest másodszorra $\displaystyle Z'$-ben. Ha belátjuk, hogy $\displaystyle Z=Z'$, akkor készen vagyunk, hiszen ekkor $\displaystyle V^*KZ\sphericalangle=V^*WZ\sphericalangle=90^{\circ}$. Jelölje $\displaystyle W'$ az $\displaystyle A'$ pont vetületét a $\displaystyle BC$ egyenesen, és jelölje $\displaystyle K'$ a $\displaystyle K$ tükörképét az Euler-egyenesre nézve. Mivel láttuk már, hogy az $\displaystyle S$ Simson-egyenese az $\displaystyle A'B'C'$ háromszögre nézve a $\displaystyle KK'$ egyenes, és $\displaystyle AS\perp B'C'$, ezért az $\displaystyle A$ pont vetülete a $\displaystyle B'C'$ egyenesre rajta fekszik a $\displaystyle KK'$ egyenesen. Ha most tükrözünk az Euler-egyenesre, akkor ez azt jelenti, hogy $\displaystyle A'$ pont vetülete a $\displaystyle BC$ egyenesre nézve, azaz $\displaystyle W'$ rajta fekszik $\displaystyle KK'$-n. Innen az is világos, hogy az $\displaystyle A'W'WV^*$ egy téglalap (hiszen $\displaystyle A'V^*\perp AT$). Most térjünk vissza a $\displaystyle (V^*KWZ')$ körre. Mivel $\displaystyle WK\perp KK'$, ezért a $\displaystyle W$-vel átellenes pont - amit $\displaystyle Y$-al jelölünk - éppen a $\displaystyle KK'$ egyenes és a $\displaystyle (V^*KWZ')$ kör $\displaystyle K$-tól különböző metszéspontja lesz. Ekkor persze $\displaystyle WZ'\perp V^*W,YZ'$, így a $\displaystyle V^*WZ'Y$ is egy téglalap. De ez csak úgy lehet, ha az $\displaystyle A'W'Z'Y$ is téglalap. Ez pedig azt jelenti, hogy $\displaystyle Z'$ és $\displaystyle A'$ egyenlő távolságra van a $\displaystyle W'Y$ egyenestől, ami éppen a $\displaystyle KK'$ egyenes. Innen azonnal következik, hogy a $\displaystyle Z'$-n átmenő $\displaystyle \mathbf{v}$ irányú egyenes az $\displaystyle AA'$ egyenes tükörképe a $\displaystyle KK'$ egyenesre (és így a $\displaystyle K$ pontra is), azaz valóban $\displaystyle Z=Z'$.

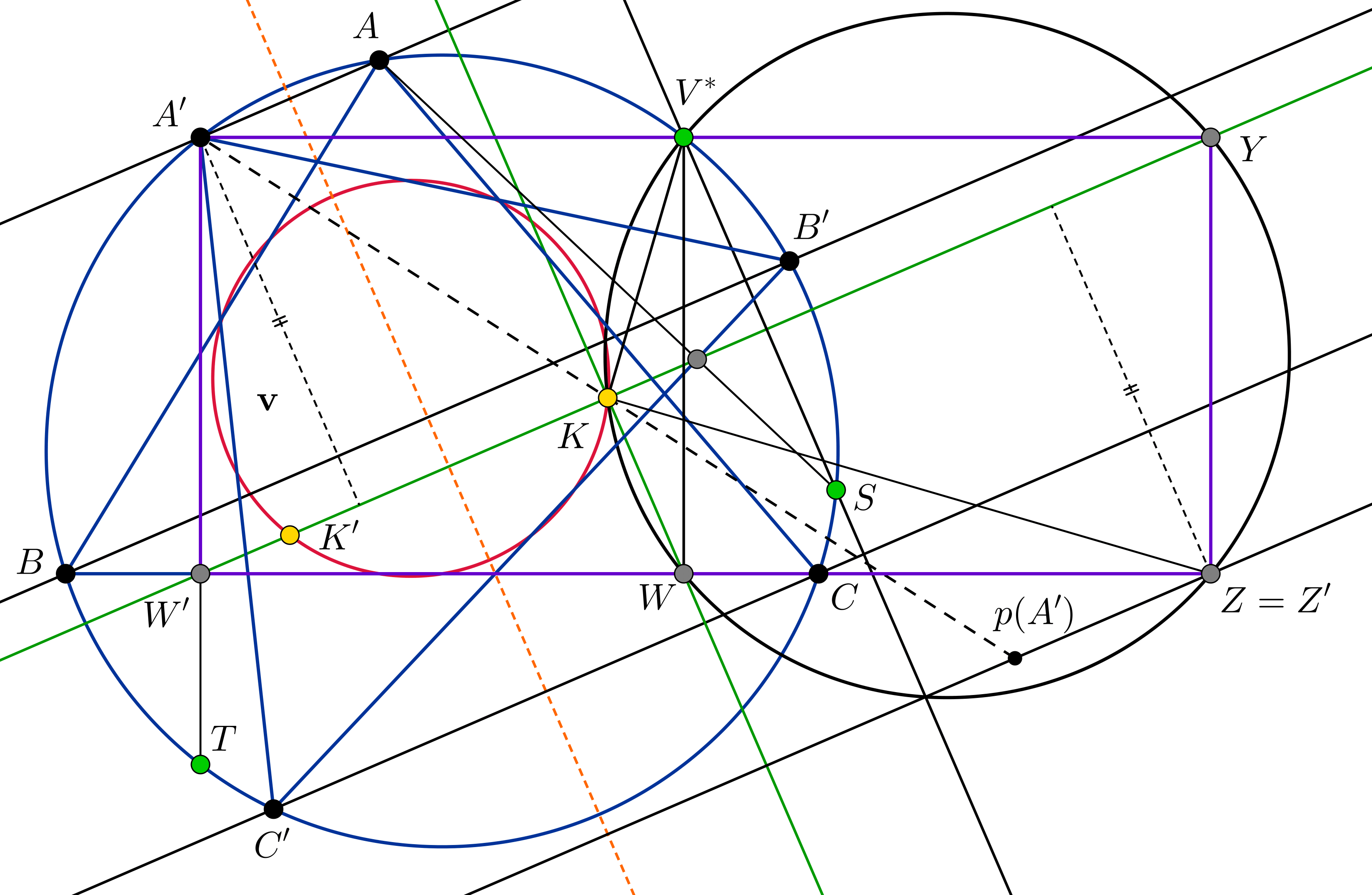
Most keressünk még egy ilyen pontot. Szerencsére nem kell sokáig keresgélni, $\displaystyle K'$ megfelelő lesz. Rögtön észrevehetjük, hogy mivel $\displaystyle KK'$ merőleges az Euler-egyenesre, a $\displaystyle p(A)p(A')\cap BC$, $\displaystyle p(B)p(B')\cap CA$, $\displaystyle p(C)p(C')\cap AB$ pontok ugyanazok, mint $\displaystyle P=K$ esetében voltak, tehát elég azt belátni, hogy az $\displaystyle Ap(A')$, $\displaystyle Bp(B')$ és $\displaystyle Cp(C')$ egyenesek egy ponton mennek át. Megmutatjuk, hogy éppen $\displaystyle H$-ban fognak találkozni. Logikai szimmetria miatt az kellene, hogy $\displaystyle Ap(A')\perp BC$. Viszont ezt már beláttuk: ha visszatükrözünk az Euler-egyenesre, ez ekvivalens azzal, hogy $\displaystyle A$ tükörképe $\displaystyle K$-ra rajta van az $\displaystyle A'$-ből $\displaystyle B'C'$-re állított merőlegesen, ami igaz lesz, mert az $\displaystyle AS$ és $\displaystyle A'H$ egyenesek párhuzamosak, és $\displaystyle K$ felezi a $\displaystyle HS$ szakaszt.

Még azt gondoljuk meg, hogy $\displaystyle K$ és $\displaystyle K'$ különböző. Csak akkor eshetne a két pont egybe, ha $\displaystyle K$ rajta lenne az Euler-egyenesen. De mivel $\displaystyle V^*$ Simson-egyenese $\displaystyle \mathbf{u}$ irányú, az Euler-egyenes lenne a Simson-egyenes, ami átmegy $\displaystyle H$-n, vagyis $\displaystyle V^*$ rajta lenne a Simson-egyenesen, de ez csak akkor lehetséges, ha egybeesik az egyik csúccsal, és ekkor az Euler-egyenes merőleges az egyik oldalra és átmegy az egyik csúcson, ami csak egyenlőszárú háromszögek esetén teljesül.

Statisztika:

9 dolgozat érkezett.
7 pontot kapott:	Keresztély Zsófia, Varga Boldizsár, Virág Tóbiás.
5 pontot kapott:	3 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	2 versenyző.

A KöMaL 2025. februári matematika feladatai