Az A. 902. feladat (2025. március)

A. 902. Az \(\displaystyle ABC\) háromszög belsejében lévő \(\displaystyle D\) pont olyan, hogy a \(\displaystyle BCD\) háromszög szabályos. Legyen \(\displaystyle E\) a \(\displaystyle D\) pont izogonális konjugáltja. Jelölje \(\displaystyle P\) azt a pontot az \(\displaystyle AB\) félegyenesen, amelyre \(\displaystyle |AP|=|BE|\). Hasonlóan, jelölje \(\displaystyle Q\) azt a pontot az \(\displaystyle AC\) félegyenesen, amelyre \(\displaystyle |AQ|=|CE|\). Mutassuk meg, hogy az \(\displaystyle AD\) egyenes felezi a \(\displaystyle PQ\) szakaszt.

Javasolta: Bán-Szabó Áron (Budapest)

(7 pont)

A beküldési határidő 2025. április 10-én LEJÁRT.

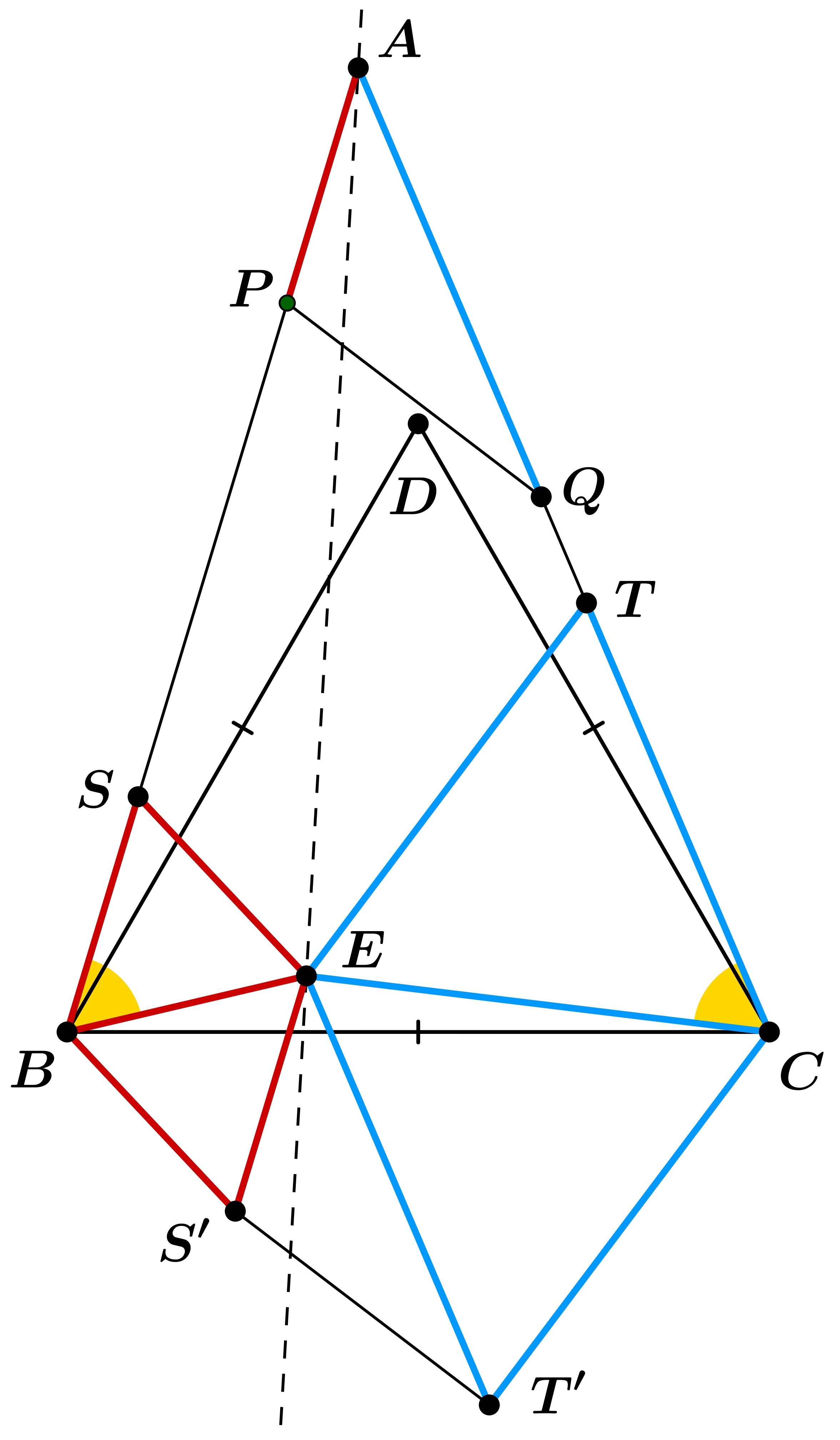
Első megoldás (szimmediánokkal): A \(\displaystyle BA,CA\) félegyeneseken vegyük fel rendre az \(\displaystyle S,T\) pontokat úgy, hogy \(\displaystyle BS=BE\) és \(\displaystyle CT=CE\) teljesüljenek. Mivel \(\displaystyle EBA\sphericalangle=EBS\sphericalangle=ECA\sphericalangle=ECT\sphericalangle=60^{\circ}\), a \(\displaystyle BES\) és \(\displaystyle CET\) háromszögek szabályosak. Vegyük fel az \(\displaystyle S'\) és \(\displaystyle T'\) pontokat úgy, hogy a \(\displaystyle BSES'\) és \(\displaystyle CTET'\) négyszögek paralelogrammák legyenek, tehát úgy, hogy a \(\displaystyle BES'\) és \(\displaystyle CET'\) háromszögek is szabályosak legyenek. Vegyük észre, hogy az \(\displaystyle ES',SB,AP\) szakaszok párhuzamosak és egyenlő hosszúak. Hasonlóan, az \(\displaystyle ET',TC,AQ\) szakaszok is párhuzamosak és egyenlő hosszúak, így az \(\displaystyle APQ\) háromszöget az \(\displaystyle \overrightarrow{AE}\) vektorral eltolva az \(\displaystyle ES'T'\) háromszöget kapjuk. Az eredeti bizonyítandó állítás az, hogy az \(\displaystyle AD\) egyenes felezi a \(\displaystyle PQ\) szakaszt. Ez ekvivalens azzal, hogy az \(\displaystyle AE\) egyenes szimmedián az \(\displaystyle APQ\) háromszögben, hiszen az \(\displaystyle AD\) és \(\displaystyle AE\) egyenesek izogonálisak. Az eltolás ezen nem változtat, így elég azt igazolni, hogy az \(\displaystyle AE\) egyenes szimmedián az \(\displaystyle ES'T'\) háromszögben. Ismert, hogy egy háromszögben egy csúcshoz tartozó szimmedián azon pontok mértani helye, amelyre a közbezáró oldalaktól való távolságok aránya egyenlő a közbezáró oldalak arányával (kicsit pontosítva két ilyen egyenes létezik, és nekünk az az egyenes kell, ami átmegy a háromszögön). Tehát elég azt igazolni, hogy \(\displaystyle d(A,ES')/d(A,ET')=ES'/ET'\), ahol \(\displaystyle d\) a távolságfüggvény. Viszont \(\displaystyle d(A,ES')=d(AB,ES')=d(SB,ES')\) hiszen az \(\displaystyle AB,ES'\) egyenesek párhuzamosak, ez pedig a szabályos háromszögek miatt éppen \(\displaystyle \dfrac{\sqrt{3}}{2}\cdot ES'\). Hasonlóan \(\displaystyle d(A,ET')=d(AC,ET')=d(TC,ET')= \dfrac{\sqrt{3}}{2}\cdot ET'\), így valóban \(\displaystyle d(A,ES')/d(A,ET')=ES'/ET'\). Készen vagyunk.

Második megoldás (mozgatásokkal): Fel fogunk használni egy ismert lemmát:
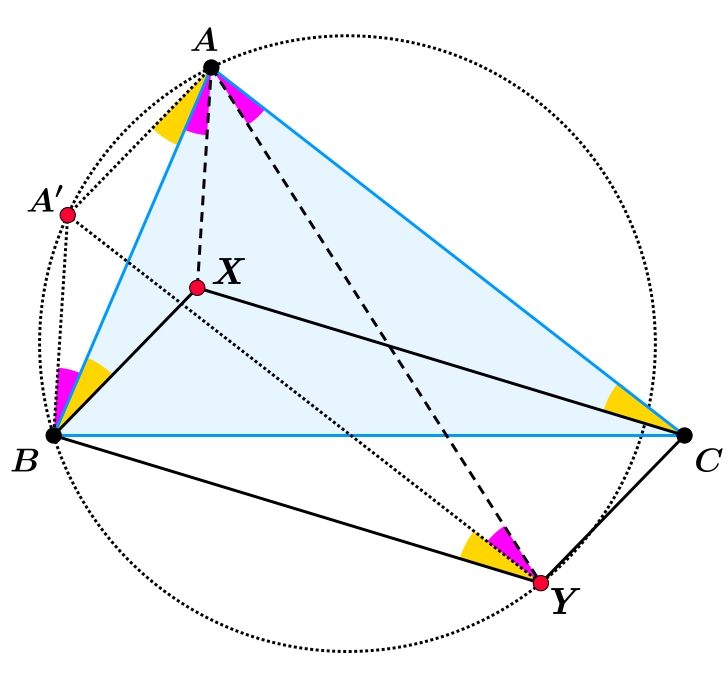
Lemma: Adott egy \(\displaystyle ABC\) háromszög (nem a feladatbeli), benne pedig egy \(\displaystyle X\) pont, amire \(\displaystyle XBA\sphericalangle =ACX\sphericalangle\). Legyen \(\displaystyle Y\) az a pont, melyre \(\displaystyle BXCY\) paralelogramma. Ekkor az \(\displaystyle X,Y\) pontok \(\displaystyle A\)-izogonálisak. Bizonyítás: Legyen \(\displaystyle A'\) az a pont, melyre az \(\displaystyle AXBA'\) és \(\displaystyle ACYA'\) négyszögek paralelogrammák. Ekkor \(\displaystyle A'AB\sphericalangle= XBA\sphericalangle= ACX\sphericalangle=A'YB\sphericalangle \), hiszen \(\displaystyle AC\parallel A'Y\) és \(\displaystyle XC\parallel BY\). Így az \(\displaystyle A,A',B,Y\) pontok egy körön vannak. Ezt felhasználva kapjuk, hogy \(\displaystyle BAX\sphericalangle=ABA'\sphericalangle=AYA'\sphericalangle=YAC\sphericalangle\). Ezzel a lemmát beláttuk.

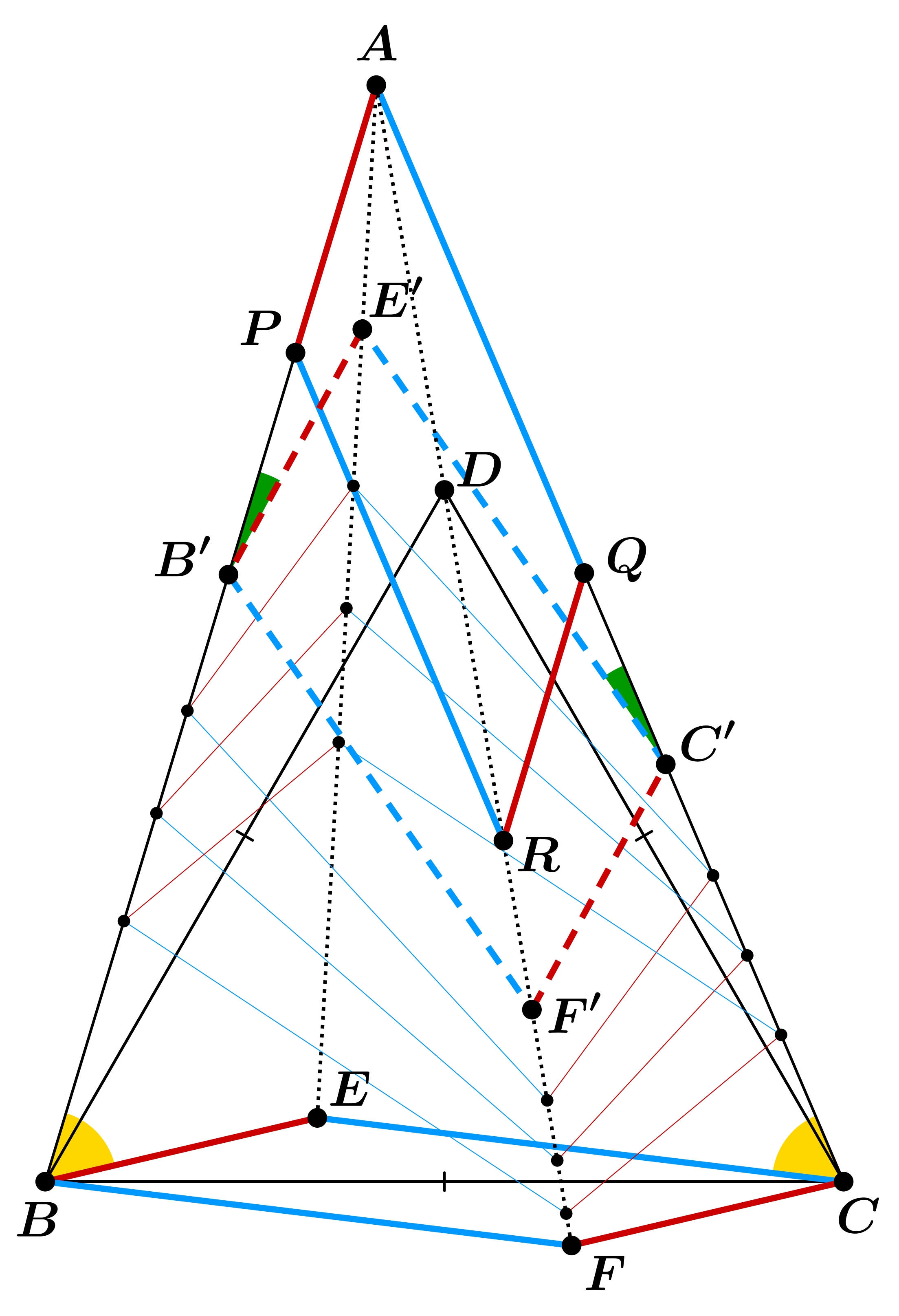
Most térjünk rá a feladatra. Jelölje \(\displaystyle F\) az \(\displaystyle E\) pont tükörképét a \(\displaystyle BC\) oldal felezőpontjára, míg jelölje \(\displaystyle R\) az \(\displaystyle A\) pont tükörképét a \(\displaystyle PQ\) felezőpontjára. Mivel \(\displaystyle EBA\sphericalangle=DBC\sphericalangle=60^{\circ}=BCD\sphericalangle=ACE\sphericalangle\), használhatjuk a lemmánkat, és azt kapjuk, hogy az \(\displaystyle AE,AF\) egyenesek \(\displaystyle A\)-izogonálisak. De mivel az \(\displaystyle AD,AE\) egyenesek is azok, elég belátni, hogy az \(\displaystyle A,R,F\) pontok egy egyenesen vannak.

Képzeljük el, hogy egy fizikai modellt építünk a feladathoz. A \(\displaystyle BECF\) paralelogramma oldalaira gondoljunk úgy, mintha pálcák lennének, melyek hossza állandó. Az \(\displaystyle AB,AC\) félegyenesekre gondoljunk sínekként, amin a \(\displaystyle B,C\) pontok mozognak. Így ha az \(\displaystyle E\) pontot kicsit mozgatjuk, akkor is egy olyan paralelogrammánk lesz, aminek oldalai \(\displaystyle BE\) és \(\displaystyle CE\) hosszúak, továbbá az egyik szemközti csúcspárja az \(\displaystyle AB,AC\) síneken van. Elég azt bebizonyítani, hogy ahogy az \(\displaystyle E\) csúcsot behúzzuk lineárisan \(\displaystyle A\)-ba, úgy az \(\displaystyle F\) pont is lineárisan tart \(\displaystyle A\)-felé, hiszen amikor \(\displaystyle E\) elmegy \(\displaystyle A\)-ba, akkor \(\displaystyle B\) elmegy \(\displaystyle P\)-be, \(\displaystyle C\) elmegy \(\displaystyle Q\)-ba és \(\displaystyle F\) elmegy \(\displaystyle R\)-be.

Tegyük fel, hogy amint húzzuk \(\displaystyle E\)-t \(\displaystyle A\)-ba, egyszer csak megállunk. Legyen ekkor a \(\displaystyle BECF\) paralelogramma képe a \(\displaystyle B'E'C'F'\) paralelogramma. Tudjuk, hogy az \(\displaystyle A-B-B'\), \(\displaystyle A-C-C'\), \(\displaystyle A-E-E'\) ponthármasok kollineárisak. Azt szeretnénk belátni, hogy az \(\displaystyle A-F-F'\) pontok is egy egyenesen vannak, ami ekvivalens azzal, hogy az \(\displaystyle AE',AF'\) egyenesek \(\displaystyle A\)-izogonálisak. Ehhez a lemmát szeretnénk használni az \(\displaystyle AB'C'\) háromszögben az \(\displaystyle E'\) pontra. Ehhez arra lenne szükség, hogy \(\displaystyle E'B'A\sphericalangle=AC'E'\sphericalangle\) teljesüljön. Használjuk fel az ismert állítást, miszerint ha két háromszögnek egy-egy oldala egyenlő hosszú, és az azzal szemközti szögek is egyenlőek, akkor a háromszögek körülírt körei egybevágóak (kerületi szögek tétele miatt). Illetve fordítva is majdnem ugyanez az állítás, ha két háromszögnek egybevágóak a körülírt körei, illetve van egy-egy ugyanolyan hosszú oldaluk, akkor ezen oldalakkal szemközti szögek vagy egyenlőek, vagy \(\displaystyle 180^{\circ}\)-ra egészítik ki egymást. Az \(\displaystyle ABE,AB'E'\) háromszögekre \(\displaystyle BE=B'E'\) és az \(\displaystyle A\)-nál lévő szögük közös, így a körülírt körei egybevágóak. Az \(\displaystyle ABE,ACE\) háromszögek \(\displaystyle AE\) oldala közös, és az azzal szemközti szögek mind \(\displaystyle 60\) fokosak, így körülírt körei egybevágóak. Végül az \(\displaystyle ACE,AC'E'\) háromszögekre is \(\displaystyle CE=C'E'\) és az \(\displaystyle A\)-nál lévő szögük közös, így körülírt körei egybevágóak. Ezzel azt kaptuk, hogy az \(\displaystyle AB'E',AC'E'\) háromszögek körülírt körei egybevágóak. Ám az \(\displaystyle AE'\) oldal közös, és könnyen látszik, hogy \(\displaystyle AB'E'\sphericalangle+E'C'A\sphericalangle\neq 180^{\circ}\), így valóban \(\displaystyle E'B'A\sphericalangle=AC'E'\sphericalangle\). Ezzel beláttuk az állítást.

Már csak egy dolgot kell átgondolni: a fenti gondolatmenet nem érvényes akkor, amikor \(\displaystyle E=A\). Viszont ahogy lineárisan húzzuk \(\displaystyle E\)-t \(\displaystyle A\)-ba, \(\displaystyle F\) az \(\displaystyle AF\) egyenesen fog mozogni, így a folytonosság miatt ha \(\displaystyle E\)-val tartunk \(\displaystyle A\)-ba, akkor az \(\displaystyle F\) olyan pontba tart, ami rajta lesz az \(\displaystyle AF\) egyenesen. Készen is vagyunk.

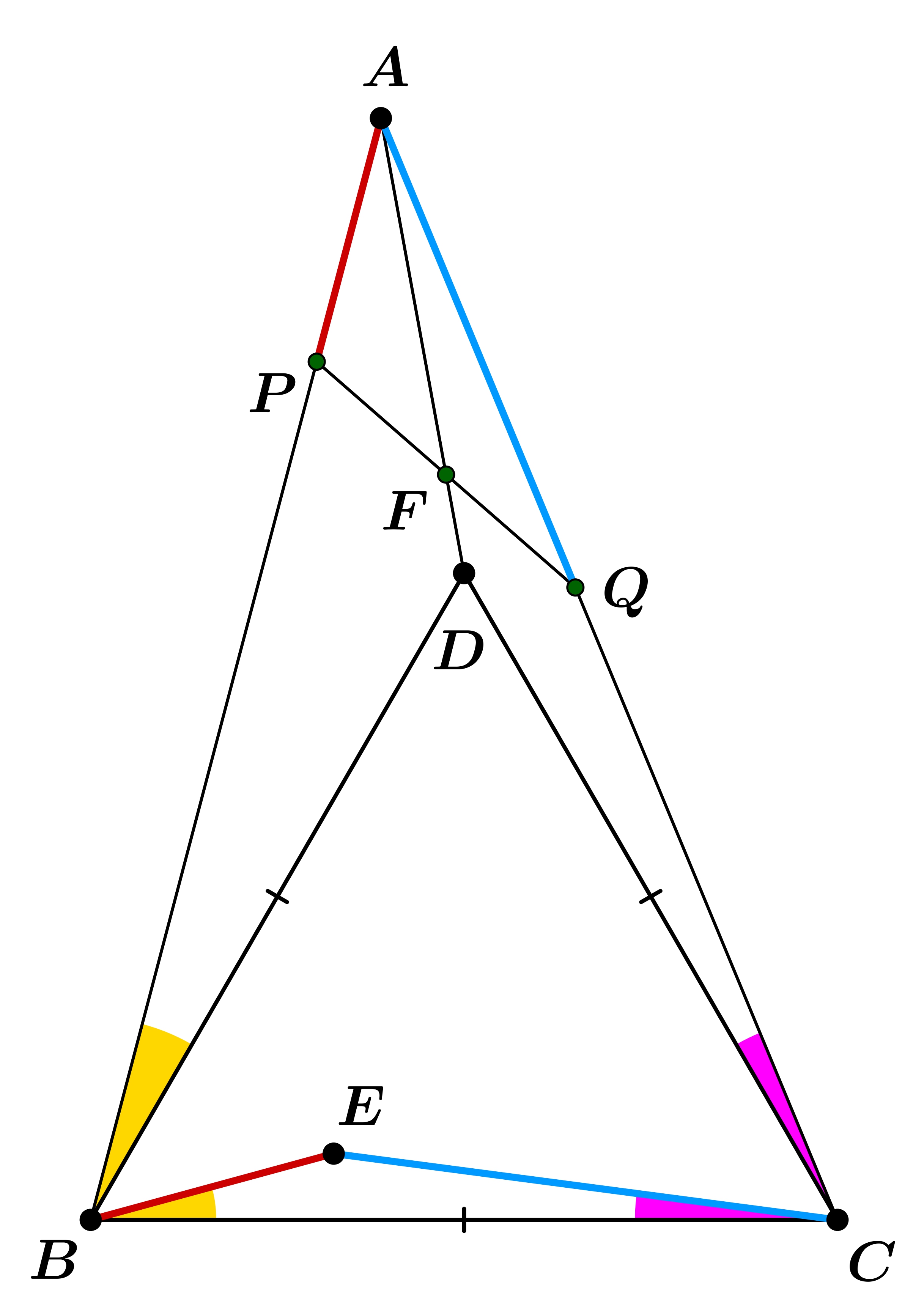
Harmadik megoldás (szinusz-tétellel): Jelölje a \(\displaystyle PQ\) és \(\displaystyle AD\) egyenesek metszéspontját \(\displaystyle F\). Azt szeretnénk igazolni, hogy \(\displaystyle PF=FQ\). Alkalmazzuk a szinusz-tételt az \(\displaystyle APF\) és \(\displaystyle AFQ\) háromszögekben:

\(\displaystyle PF=AF \cdot \frac{\sin PAF \sphericalangle}{\sin FPA \sphericalangle}, \quad FQ=AF \cdot \frac{\sin FAQ \sphericalangle}{\sin AQF \sphericalangle}.\)

Tehát elég azt igazolnunk, hogy \(\displaystyle \frac{\sin PAF \sphericalangle}{\sin FPA \sphericalangle}=\frac{\sin FAQ \sphericalangle}{\sin AQF \sphericalangle}\), amit átrendezve a \(\displaystyle \frac{\sin AQF \sphericalangle}{\sin FPA \sphericalangle}=\frac{\sin FAQ \sphericalangle}{\sin PAF \sphericalangle}\) bizonyítandóhoz jutunk.

Az \(\displaystyle APQ\) háromszögben felírt szinusz-tétel szerint, és használva, hogy \(\displaystyle AP=BE\) és \(\displaystyle AQ=CE\),

\(\displaystyle \frac{BE}{CE}=\frac{AP}{AQ}=\frac{\sin AQP \sphericalangle}{\sin QPA \sphericalangle}=\frac{\sin AQF \sphericalangle}{\sin FPA \sphericalangle}.\)

Tehát arra vezettük vissza a feladat állítását, hogy \(\displaystyle \frac{BE}{CE}=\frac{\sin FAQ \sphericalangle}{\sin PAF \sphericalangle}\).

Most alkalmazzuk a szinusz-tételt a \(\displaystyle BEC\) háromszögben, és használjuk ki az izogonális konjugálás definícióját, miszerint \(\displaystyle CBE \sphericalangle=DBA \sphericalangle\) és \(\displaystyle ECB \sphericalangle=ACD \sphericalangle\). Azt kapjuk, hogy

\(\displaystyle \frac{BE}{CE}=\frac{\sin ECB \sphericalangle}{\sin CBE \sphericalangle}=\frac{\sin ACD \sphericalangle}{\sin DBA \sphericalangle}.\)

Ezzel a bizonyítandót a \(\displaystyle \frac{\sin FAQ \sphericalangle}{\sin PAF \sphericalangle}=\frac{\sin ACD \sphericalangle}{\sin DBA \sphericalangle}\) azonosságra vezettük vissza, amit átrendezve, és azonos szögeket beírva, a \(\displaystyle \frac{\sin DAC \sphericalangle}{\sin ACD \sphericalangle}=\frac{\sin BAD \sphericalangle}{\sin DBA \sphericalangle}\) egyenletet kapjuk.

Használva, hogy a \(\displaystyle BCD\) szabályossága miatt \(\displaystyle BD=CD\), a bizonyítandó következik az \(\displaystyle ACD\) és \(\displaystyle ADB\) háromszögekben felírt szinusz-tételekből:

\(\displaystyle \frac{\sin DAC \sphericalangle}{\sin ACD \sphericalangle}=\frac{CD}{AD}=\frac{BD}{AD}=\frac{\sin BAD \sphericalangle}{\sin DBA \sphericalangle}.\)

Ezzel a bizonyítást befejeztük.

Statisztika:

14 dolgozat érkezett.
7 pontot kapott:	Aravin Peter, Bodor Mátyás, Bui Thuy-Trang Nikolett, Czanik Pál, Forrai Boldizsár, Holló Martin, Keresztély Zsófia, Sha Jingyuan, Szakács Ábel, Varga Boldizsár, Virág Tóbiás.
6 pontot kapott:	Tianyue DAI, Xiaoyi Mo.
0 pontot kapott:	1 versenyző.

A KöMaL 2025. márciusi matematika feladatai