 |
Az A. 906. feladat (2025. április) |
A. 906. Nevezzük \(\displaystyle \mathcal{V}_c\)-nek azt a végtelen párhuzamos vonalzót, amelynek párhuzamos éleinek távolsága \(\displaystyle c\). Egy \(\displaystyle \mathcal{V}_c\) vonalzóval az alábbi szerkesztési lépések végezhetőek el:
\(\displaystyle \bullet\) két különböző ponton átmenő egyenes megszerkesztése;
\(\displaystyle \bullet\) adott \(\displaystyle l\) egyenesre olyan \(\displaystyle l\)-el párhuzamos \(\displaystyle l'\) egyenes megszerkesztése, amelyre \(\displaystyle l\) és \(\displaystyle l'\) távolsága \(\displaystyle c\) (két ilyen egyenes létezik minden \(\displaystyle l\)-re, és mindkét egyenes megszerkeszthető ezzel a lépéssel);
\(\displaystyle \bullet\) adott \(\displaystyle A,B\) pontokra, ha \(\displaystyle |AB|\geq c\), akkor két olyan párhuzamos egyenes megszerkesztése, melyek közül az egyik átmegy \(\displaystyle A\)-n, a másik \(\displaystyle B\)-n, és az egyenesek távolsága \(\displaystyle c\) (itt is két lehetséges megoldás van amennyiben \(\displaystyle |AB|>c\), és ezzel a lépéssel mindkettő megszerkeszthető).
Egy kör alakú lap határán adott három pont, melyek egy nem egyenlő szárú háromszöget határoznak meg. Legyen \(\displaystyle n\) egy pozitív egész szám. Bizonyítsuk be, hogy a három felvett pont és az \(\displaystyle n\) szám függvényében létezik olyan \(\displaystyle C>0\) szám, amelyre bármely \(\displaystyle 0<c\leq C\)-re meg lehet szerkeszteni \(\displaystyle n\) darab olyan pontot csak egy \(\displaystyle \mathcal{V}_c\) használatával, amely rajta fekszik a háromszögnek valamelyik hozzáírt körén.
A lapon kívül nem tudunk szerkeszteni. A lap határán lehet szerkeszteni, fel lehet venni egy egyenes és a lap határának a metszéspontját.
Javasolta: Bán-Szabó Áron (Budapest)
(7 pont)
A beküldési határidő 2025. május 12-én LEJÁRT.
Először is néhány fontos szerkesztési lemmát fogunk belátni, melyeknél feltételezzük, hogy van valamilyen \(\displaystyle \mathcal{V}_c\) vonalzónk (kellően pici \(\displaystyle c\)-vel). Nevezzük el a három adott pont körülírt körét \(\displaystyle \Omega\)-nak. Először végigmegyünk a fő szerkesztési lépéseken, és csak a bizonyítás végén látjuk be a feladat szövegében lévő \(\displaystyle C\) szám létezését hozzá.
1. Lemma: Ha adott egy \(\displaystyle P\) pont \(\displaystyle \Omega\) belsejében és egy \(\displaystyle \ell\) egyenes, ami elmetszi két pontban \(\displaystyle \Omega\)-t, akkor tudunk \(\displaystyle P\)-n átmenő \(\displaystyle \ell\)-el párhuzamos egyenest szerkeszteni.
Vegyünk egy \(\displaystyle \ell\)-el párhuzamos egyenest (a vonalzónk segítségével), majd azon vegyünk fel három pontot, \(\displaystyle A\)-t, \(\displaystyle B\)-t és \(\displaystyle C\)-t úgy, hogy \(\displaystyle B\) az \(\displaystyle AC\) felezőpontja legyen. Ezt meg tudjuk csinálni, ha veszünk egy tetszőleges egyenest (ami nem párhuzamos \(\displaystyle \ell\)-el), és megszerkesztjük mindkét tőle \(\displaystyle c\) távolságra lévő vele párhuzamos egyenest, majd megnézzük hol metszi el ez a három egyenes a mi \(\displaystyle \ell\)-el párhuzamosunkat. Messék el a \(\displaystyle PA,PB\) egyenesek \(\displaystyle \ell\)-et \(\displaystyle A'\)-ben és \(\displaystyle B'\)-ben. Az \(\displaystyle A'B,B'C\) egyenesek metszéspontja legyen \(\displaystyle Q\). Azt állítjuk, hogy \(\displaystyle PQ\parallel \ell\). Ez abból következik, hogy \(\displaystyle PB/BB'=AB/(A'B'-AB)=BC/(A'B'-BC)=QB/BA'\), tehát az \(\displaystyle BB'A'\) és \(\displaystyle BPQ\) háromszögek hasonlóak, így az \(\displaystyle A'B'\) és \(\displaystyle PQ\) párhuzamosak.
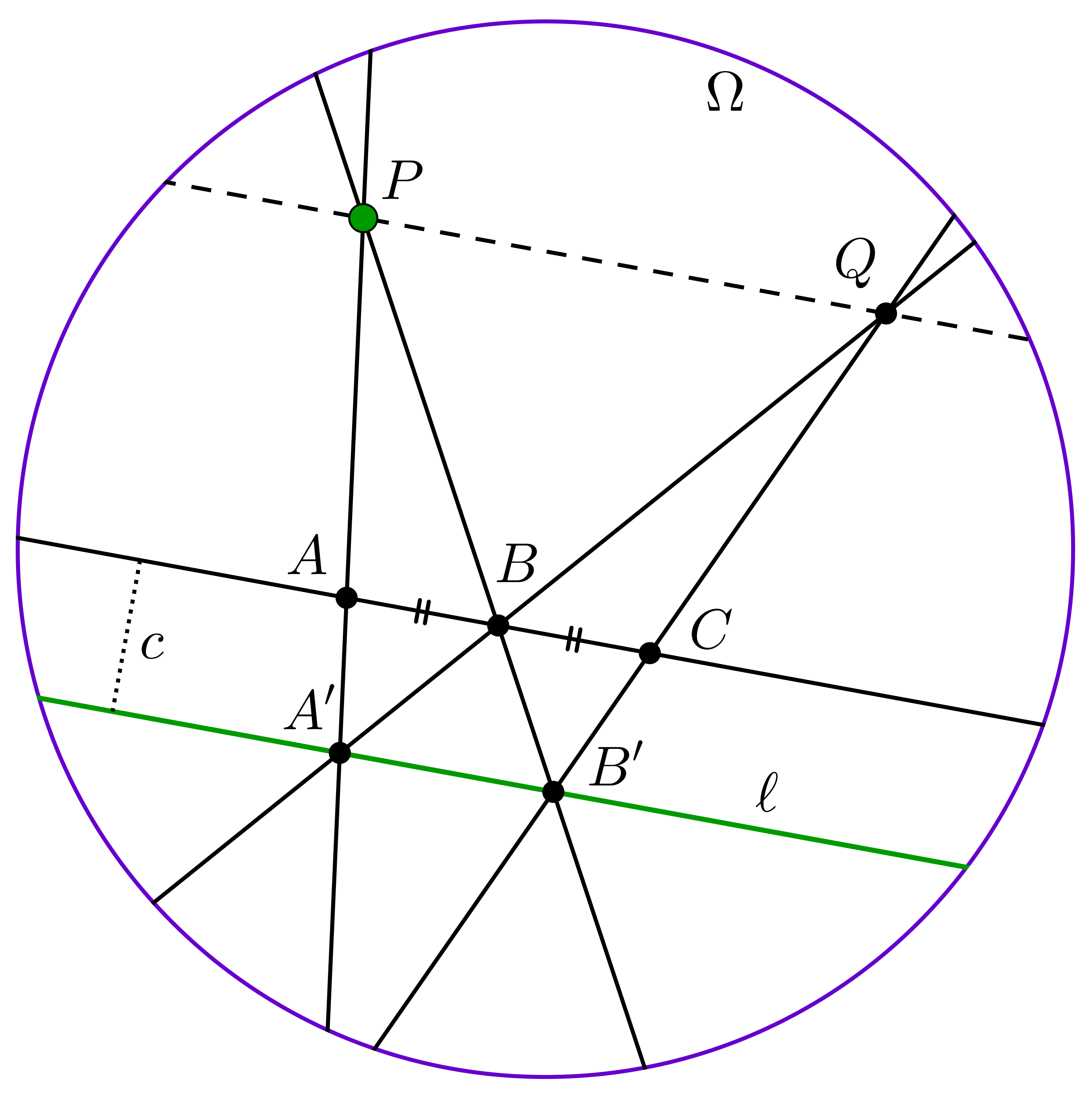
2. Lemma: Meg tudjuk szerkeszteni bármilyen \(\displaystyle \Omega\) belsejébe vagy határára eső \(\displaystyle AB\) szakasz felezőpontját.
Vegyünk fel a vonalzó segítségével egy \(\displaystyle AB\)-vel párhuzamos egyenest, illetve rajta \(\displaystyle A'\), \(\displaystyle F'\), \(\displaystyle B'\) pontokat úgy, hogy \(\displaystyle F'\) felezze az \(\displaystyle A'B'\) szakaszt (hasonlóan, mint előbb). Legyen \(\displaystyle M=AA'\cap BB'\). Ekkor az \(\displaystyle MF'\) egyenes az \(\displaystyle AB\) szakaszt a felezőpontjában fogja elmetszeni.
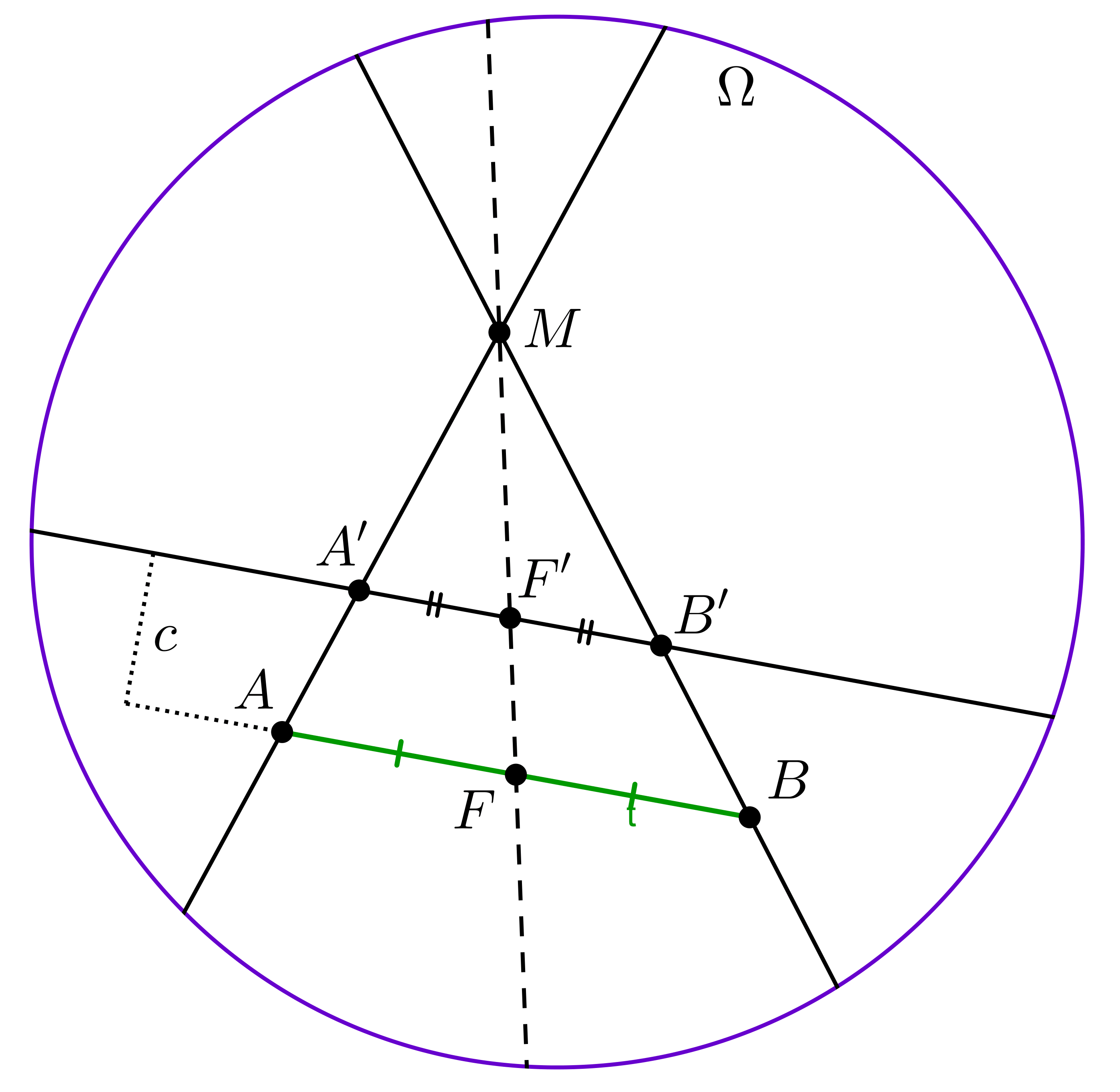
3. Lemma: Tudunk \(\displaystyle \Omega\) belsejében pontot tükrözni másikra, feltéve, hogy a tükörkép is \(\displaystyle \Omega\) belsejébe esik.
Lényegében ugyanaz, mint a 2. Lemma csak most \(\displaystyle F\) az adott és \(\displaystyle B\)-t kell megkapjuk.
4. Lemma: Meg tudjuk szerkeszteni \(\displaystyle \Omega\) középpontját, és így tudunk merőlegest szerkeszteni bármilyen \(\displaystyle \Omega\)-ban lévő pontból bármely \(\displaystyle \Omega\)-t kétszer elmetsző egyenesbe.
Tudunk szerkeszteni párhuzamos húrpárokat. Egy pár szakaszfelező pontjait összekötő egyenese éppen a szakaszfelező merőleges lesz, így két ilyen pár felezőmerőlegeseinek metszéspontjából megkapjuk a középpontot. Innen a merőleges szerkesztése következik az 1. és 2. Lemmából, hiszen az egyenesünkből vesszük az \(\displaystyle \Omega\)-ba eső húrt, arra merőlegest állítunk a kör középpontjából (ami igazából a húr felezőpontjának megszerkesztése), és aztán párhuzamost húzunk.
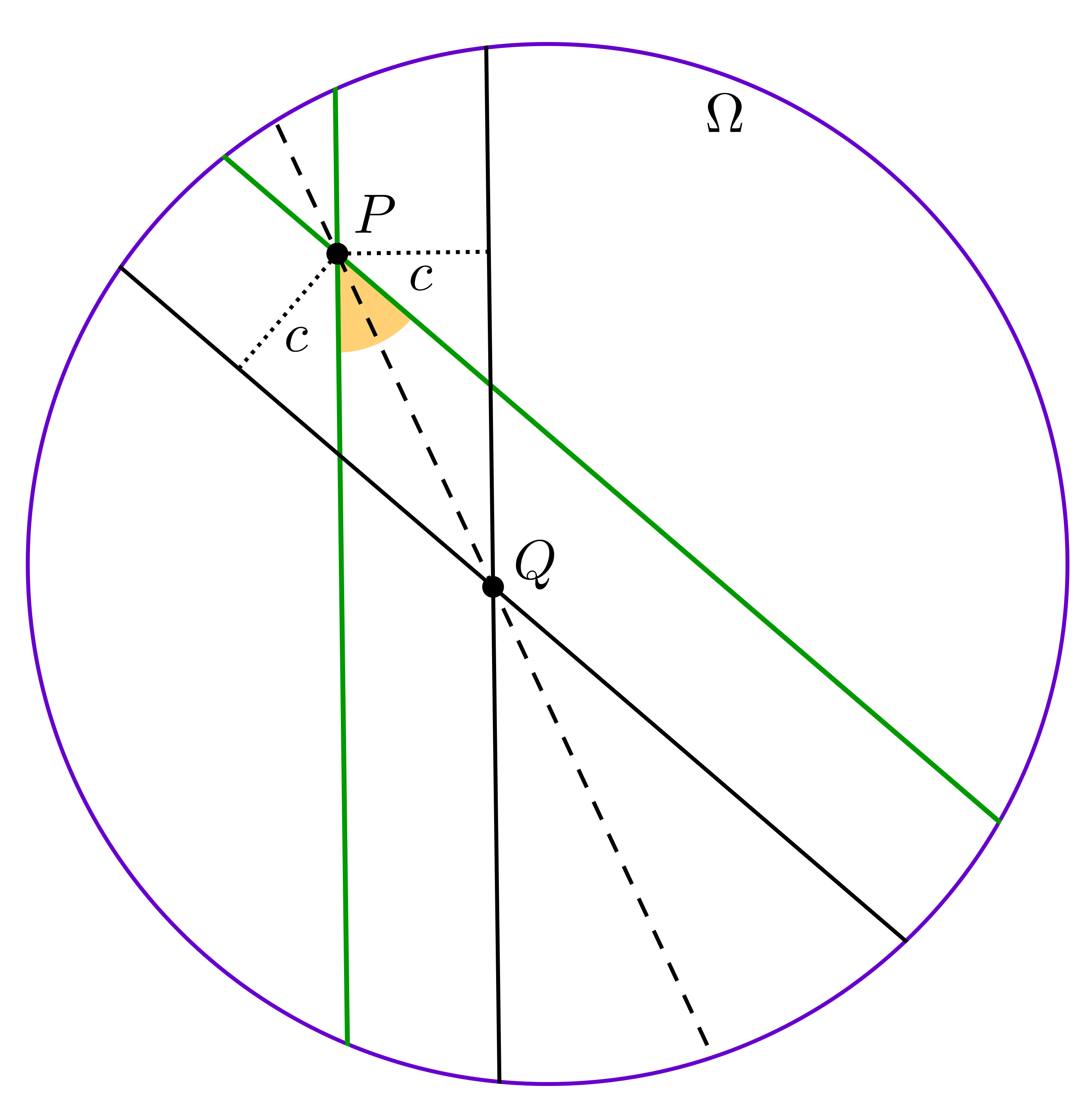
5. Lemma: Tudunk szögfelezőt szerkeszteni, ha a két egyenes metszéspontja a kör belsejébe esik.
Vegyük fel az adott szögtartományban az egyenesektől \(\displaystyle c\)-re lévő egyeneseket. Ezek metszéspontja rajta lesz a szögfelezőn.
Most térjünk rá az \(\displaystyle n\) pont megszerkesztésére. Tegyük fel, hogy a \(\displaystyle B,C\) csúcsoknál hegyesszögek vannak (ez feltehető, mert legfeljebb egy \(\displaystyle \geq 90^{\circ}\)-os szöge lehet egy háromszögnek). Az \(\displaystyle A\)-hoz tartozó hozzáírt körön meg fogunk szerkeszteni először három, majd abból tetszőlegesen sok pontot.
Szerkesszük meg a háromszög beírt körének \(\displaystyle I\) középpontját (két szögfelező metszéspontja). Állítsunk merőlegest \(\displaystyle I\)-ből \(\displaystyle BC\)-re, ez lesz \(\displaystyle D\), a beírt kör érintési pontja \(\displaystyle BC\)-n. Ezután szerkesszük meg a \(\displaystyle BC\) oldal \(\displaystyle M\) felezőpontját, aminek hála a 3. Lemma segítségével meg tudjuk kapni \(\displaystyle E\)-t, a \(\displaystyle D\) pont tükörképét \(\displaystyle M\)-re nézve, az \(\displaystyle A\)-hoz tartozó hozzáírt kör érintési pontját \(\displaystyle BC\)-n.
Következőnek állítsunk merőlegest \(\displaystyle E\)-ből az \(\displaystyle AD\) egyenesre, ennek a talppontja legyen \(\displaystyle T\). Mivel a \(\displaystyle B,C\) csúcsoknál hegyesszögek vannak, \(\displaystyle T\in \Omega\). Belátjuk, hogy \(\displaystyle T\) is rajta van a hozzáírt körön. Képzeljük el, hogy a beírt kört \(\displaystyle A\)-ból belenagyítjuk a hozzáírt körbe. Ismert, hogy ha a beírt kör \(\displaystyle D\)-vel átellenes pontja \(\displaystyle D'\), akkor \(\displaystyle D'\) képe \(\displaystyle E\) lesz a nagyítás után. Mi lesz \(\displaystyle T\)-nek az ősképe? Természetesen \(\displaystyle E\) ősképének, azaz \(\displaystyle D'\)-nek a vetülete az \(\displaystyle AD\) egyenesre nézve. Viszont \(\displaystyle DD'\) átmérője a beírt körnek, így \(\displaystyle T\) ősképe rajta van a beírt körön, tehát \(\displaystyle T\) is rajta van a hozzáírt körön.
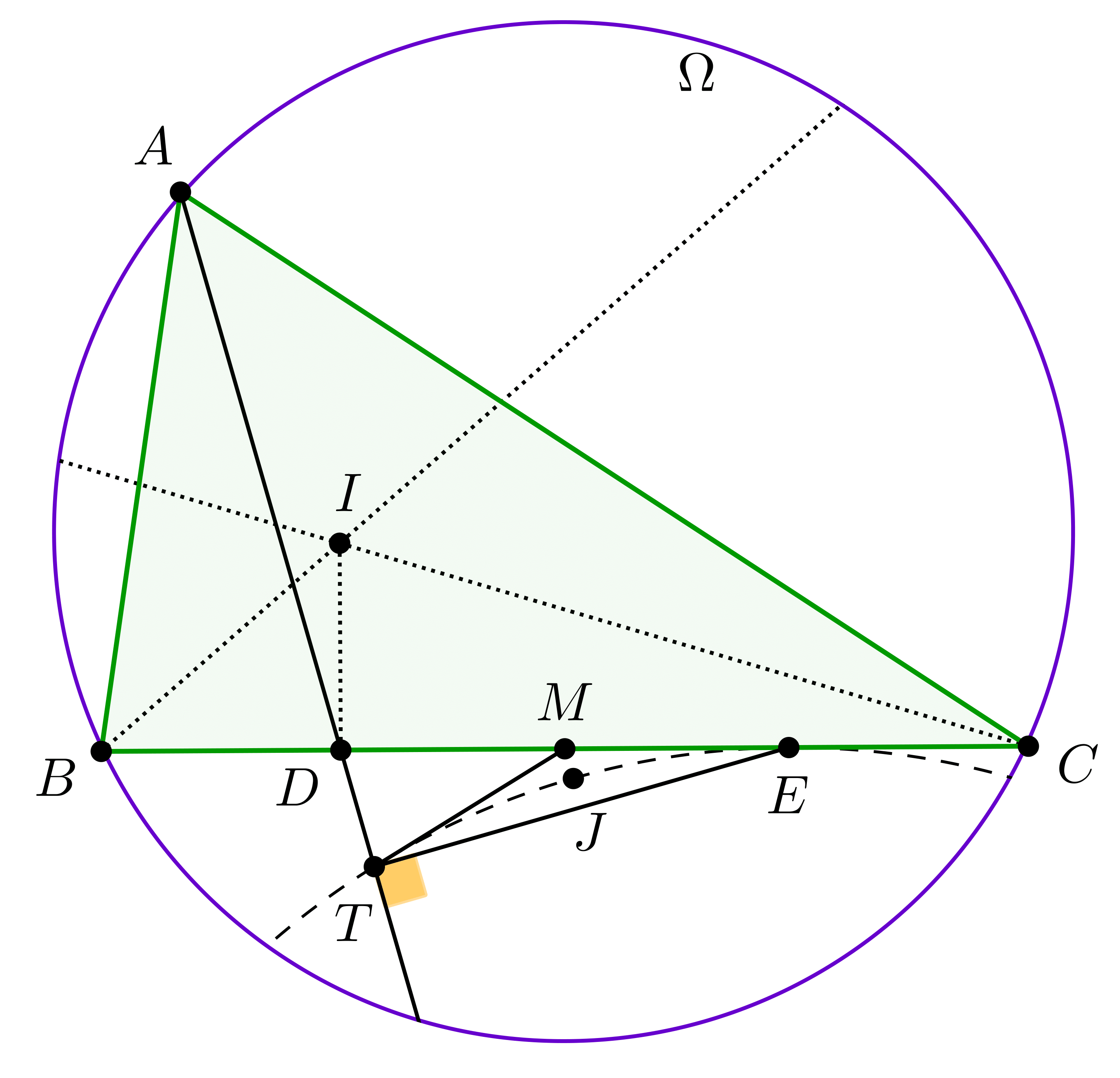
Most szerkesszük meg az \(\displaystyle MTE\) háromszög beírt körének középpontját, ez legyen \(\displaystyle J\). Belátjuk, hogy \(\displaystyle J\) is rajta van a hozzáírt körön. Először is \(\displaystyle MT=ME\), hiszen az \(\displaystyle EDT\) derékszögű háromszögben \(\displaystyle M\) az \(\displaystyle ED\) átfogó felezőpontja. Így \(\displaystyle EJT\sphericalangle=180^{\circ}-MET\sphericalangle\), ami az érintőszárú kerületi szögek tétele miatt éppen az \(\displaystyle ET\) húr kerületi szöge. Tehát valóban \(\displaystyle J\) is rajta van.
Innentől pedig egyszerű a dolgunk. Minden lépésben megszerkesztjük valamelyik (mondjuk a legkisebb) körív felezőpontját. Hogyan? Ha mondjuk a \(\displaystyle JET\) háromszög \(\displaystyle JT\)-hez tartozó ívfelezőpontját szeretnénk, csupán megszerkesztjük az \(\displaystyle E\)-hez tartozó belső szögfelezőt és a \(\displaystyle JT\) szakasz felezőmerőlegesét, ezek pont ott metszik egymást.
Csupán azt kell még meggondolnunk, hogy ha \(\displaystyle c\) elég kicsi, akkor a fenti szerkesztési lépések valóban elvégezhetőek.
Az 1. Lemmában az egyetlen probléma az lehetne, ha \(\displaystyle Q\) a körön kívülre esne. Vegyük észre, hogy a \(\displaystyle PQ\) távolság az \(\displaystyle A'AB,A'PQ\) háromszögek hasonlósága miatt \(\displaystyle \dfrac{d(\ell,PQ)}{d(\ell,AB)}\cdot AB\). Ha \(\displaystyle Q\) \(\displaystyle \Omega\)-n kívül esne, akkor az \(\displaystyle AB\) egyenessel is szerkesszünk egy vele párhuzamos, tőle \(\displaystyle c\) távolságra lévő egyenest, majd hajtsuk végre ugyanazokat a lépéseket. Ekkor \(\displaystyle d(\ell,PQ)\) fix, és \(\displaystyle d(\ell,AB)\) növekszik, így csökken a \(\displaystyle PQ\) távolság. Látható, hogy ha \(\displaystyle c\) elég kicsi, akkor véges sok próba után biztos, hogy a \(\displaystyle PQ\) távolság elég kicsi lesz.
A 2. Lemmánál arra kell ügyeljünk, hogy \(\displaystyle M\) benne legyen a körben. Ha képzeletben az \(\displaystyle A',F',B'\) pontokat mozgatnánk az \(\displaystyle A'B'\) egyenesen úgy, hogy az \(\displaystyle A'F'=F'B'\) távolság fix maradjon, akkor \(\displaystyle M\) egy \(\displaystyle AB\)-vel párhuzamos egyenesen mozogna. Persze folytonosan nem tudunk mozgatni, de azt megtehetjük, hogy \(\displaystyle A'\)-t az \(\displaystyle F'\) helyére választjuk, illetve \(\displaystyle F'\)-t a \(\displaystyle B'\) helyére (valamint a másik irányba is eljátszható). Először is \(\displaystyle c\)-t válasszuk olyannak, hogy ez az egyenes elmesse a kört két pontban. Másodsorban pedig gondoljuk meg, hogy ha \(\displaystyle c\) elég kicsi, akkor ahogy végigmegyünk a sok lehetséges \(\displaystyle A',F',B'\) ponthármason (az \(\displaystyle A'F'=F'B'\) távolság fix), akkor \(\displaystyle M\) olyan kicsiket mozdul el, hogy valahol biztosan a körbe fog esni.
A 3. és 4. Lemmáknál az előző lépésekből használunk véges sokat, így itt nincs teendőnk.
Az 5. Lemmánál csak arra kell figyelni, hogy \(\displaystyle Q\) a körbe essen, és világos, hogy elég kicsi \(\displaystyle c\)-re a \(\displaystyle PQ\) távolság bármilyen kicsi lehet.
Statisztika:
7 dolgozat érkezett. 7 pontot kapott: Aravin Peter, Bodor Mátyás, Forrai Boldizsár, Varga Boldizsár, Xiaoyi Mo. 5 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2025. áprilisi matematika feladatai
