Az A. 910. feladat (2025. május)

A. 910. Adottak az \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\), \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\) pontok ebben a sorrendben egy egyenesen. Az \(\displaystyle A_1A_2\) és \(\displaystyle B_1B_2\) átmérőjű félkörök \(\displaystyle P\)-ben, a \(\displaystyle B_1B_2\) és \(\displaystyle C_1C_2\) átmérőjű félkörök \(\displaystyle Q\)-ban, és a \(\displaystyle C_1C_2\) és \(\displaystyle A_1A_2\) átmérőjű félkörök \(\displaystyle R\)-ben metszik egymást. A \(\displaystyle k\), \(\displaystyle l\) körök mindhárom félkört érintik az ábrán látható módon. Jelöljük \(\displaystyle k\) és az \(\displaystyle A_1A_2\) átmérőjű félkör érintési pontját \(\displaystyle K\)-val, míg \(\displaystyle l\) és a \(\displaystyle C_1C_2\) átmérőjű félkör érintési pontját \(\displaystyle L\)-lel.

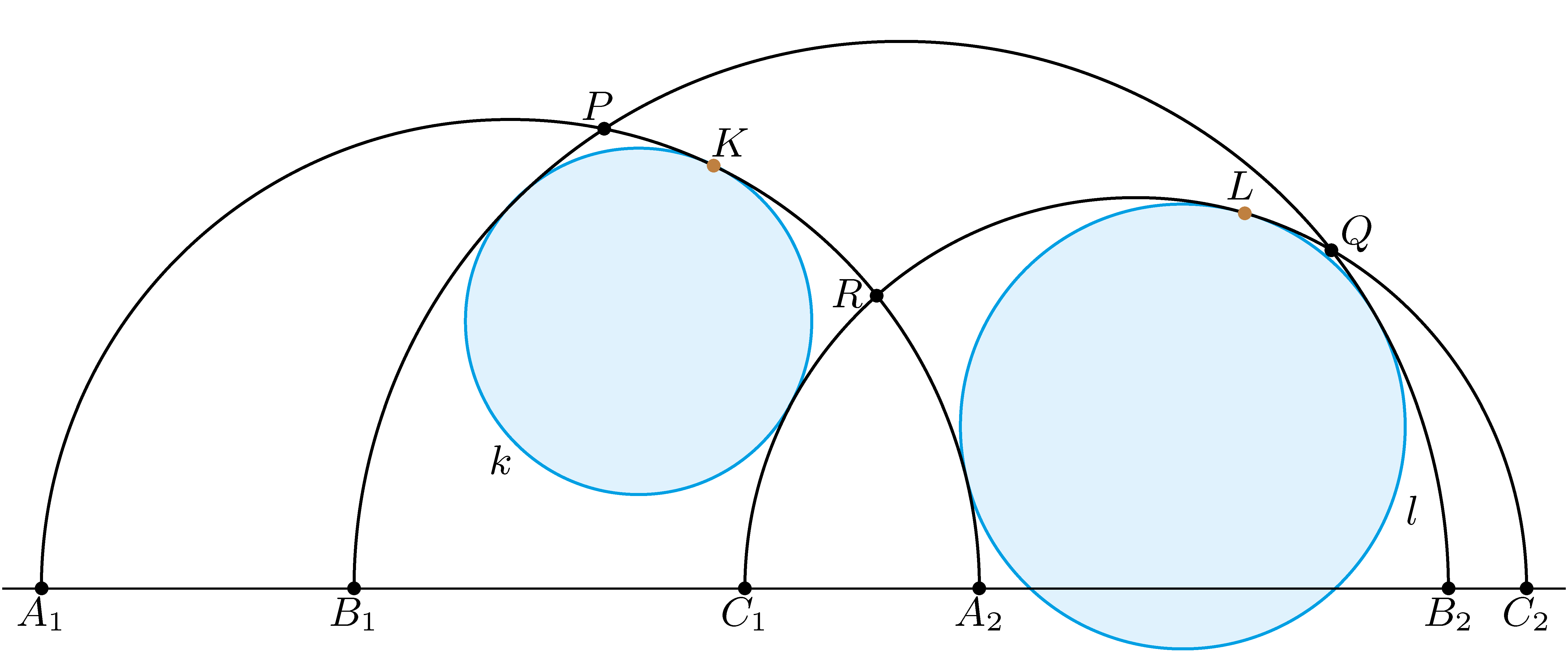
Bizonyítsuk be, hogy

\(\displaystyle \dfrac{A_1R\cdot B_1P\cdot B_2Q\cdot C_2R}{A_2R\cdot B_1Q\cdot B_2P\cdot C_1R}=\dfrac{A_1K\cdot C_2L}{A_2K\cdot C_1L}. \)

Javasolta: Bán-Szabó Áron (Budapest)

(7 pont)

A beküldési határidő 2025. június 10-én LEJÁRT.

Jelöljük az \(\displaystyle A_1B_1C_1A_2B_2C_2\) egyenest \(\displaystyle e\)-vel. Vegyük észre, hogy a bizonyítandó állítás átírható

\(\displaystyle \dfrac{A_1R\cdot A_2K}{A_1K\cdot A_2R}\cdot \dfrac{C_1L\cdot C_2R}{C_1R\cdot C_2L}=\dfrac{B_1Q\cdot B_2P}{B_1P\cdot B_2Q}\)

alakba, ami nem más, mint

\(\displaystyle (A_1,A_2;R,K)\cdot (C_1,C_2;R,L)=(B_1,B_2;Q,P),\)

ahol \(\displaystyle (A,B;C,D)=\dfrac{AC\cdot BD}{AD\cdot BC}\) az \(\displaystyle ABCD\) pontnégyes kettősviszonyát jelöli.

Ez inspirálhatja, hogy vezessünk be egy \(\displaystyle \mathcal{D}\) függvényt az \(\displaystyle e\) egyenes feletti pontokon, ami bármely \(\displaystyle X,Y\) pontpárhoz (amelyek az \(\displaystyle e\) egyenes felett helyezkednek el) a

\(\displaystyle \mathcal{D}(X,Y): =(E_2,E_1;X,Y)\)

kettősviszonyt rendeli hozzá, ahol \(\displaystyle E_1,E_2\) azok a pontok az \(\displaystyle e\) egyenesen, amelyre az \(\displaystyle E_1,X,Y,E_2\) pontok ebben a sorrendben helyezkednek el az \(\displaystyle E_1E_2\) átmérőjű félkörön. Ilyen félkör egyértelműen létezik, hiszen az \(\displaystyle XY\) szakasz felezőmerőlegesének és \(\displaystyle e\)-nek a metszéspontja meghatározza a középpontot. (Ez így még nem teljesen elég, hiszen ez a félkör csak akkor létezik, ha \(\displaystyle XY\not\perp e\), viszont az \(\displaystyle e\perp XY\) esetben definiálhatjuk \(\displaystyle \mathcal{D}(X,Y)\)-t az \(\displaystyle EX/EY\) arányként, ahol \(\displaystyle E=XY\cap e\) és az \(\displaystyle E,Y,X\) pontok ebben a sorrendben vannak az \(\displaystyle XY\) egyenesen. Most már könnyű ellenőrizni, hogy a függvényünk valóban egyértelmű az \(\displaystyle e\) egyenes feletti pontpárokra.)

Az lenne ideális számunkra, ha ez egy távolságfüggvény lenne. Csakhogy \(\displaystyle \mathcal{D}(X,Y)\) mindig egy \(\displaystyle 1\)-nél nem kisebb szám, illetve nem teljesül az sem, hogy egy \(\displaystyle e\)-n fekvő félkörön (ami nálunk egyenesként funkcionál) additív \(\displaystyle \mathcal{D}\). Ezt most kijavítjuk: legyen

\(\displaystyle \| XY\|:=\ln(\mathcal{D}(X,Y)).\)

Vegyük észre, hogy ez már egy valódi távolság lesz, hiszen nemnegatív, szimmetrikus, \(\displaystyle e\)-n fekvő félkörökön additív, és ellenőrizhető, hogy teljesíti a háromszög-egyenlőtlenséget is. Fontos kihangsúlyozni, hogy a \(\displaystyle \|.\|\) távolsággal az \(\displaystyle e\) egyenes feletti félsíkon az egyenesek éppen az \(\displaystyle e\)-n fekvő félkörök. Azaz a legrövidebb út definíció szerint két pont között azon a félkörön (vagy \(\displaystyle e\)-re merőleges egyenesen) van, ami \(\displaystyle e\)-n fekszik és átmegy a két ponton. Kettő kulcslemmára lesz csak szükségünk:

1. Lemma: \(\displaystyle \|.\|\) additív az \(\displaystyle e\)-n fekvő félkörökön, azaz ha az \(\displaystyle E_1,X,Y,Z,E_2\) pontok ebben a sorrendben fekszenek az \(\displaystyle E_1E_2\) átmérőjú körön (ahol \(\displaystyle E_1,E_2\in e\)), akkor \(\displaystyle \|XY\|+\|YZ\|=\|XZ\|\).

Bizonyítás: Csak vegyük észre, hogy

\(\displaystyle \ln \left (\dfrac{E_1Y\cdot E_2X}{E_1X\cdot E_2Y}\right)+\ln \left (\dfrac{E_1Z\cdot E_2Y}{E_1Y\cdot E_2Z}\right)=\ln \left (\dfrac{E_1Y\cdot E_2X\cdot E_1Z\cdot E_2Y}{E_1X\cdot E_2Y\cdot E_1Y\cdot E_2Z}\right)=\ln \left (\dfrac{E_1Z\cdot E_2X}{E_1X\cdot E_2Z}\right).\qquad \square\)

2. Lemma: Legyen \(\displaystyle \Omega\) egy kör, aminek középpontja \(\displaystyle e\) felett van. Tegyük fel, hogy az \(\displaystyle X\) és az \(\displaystyle Y_1,Y_2\in \Omega\) pontok olyanok, amik \(\displaystyle e\) felett vannak és az \(\displaystyle XY_1,XY_2\) egyenesek (azaz \(\displaystyle e\)-n fekvő félkörök) érintik \(\displaystyle \Omega\)-t. Ekkor \(\displaystyle \|XY_1\|=\|XY_2\|\).

Bizonyítás: Tekintsük azt az \(\displaystyle \omega\) kört, ami átmegy \(\displaystyle X\)-en, szimmetrikus \(\displaystyle e\)-re és merőleges az \(\displaystyle \Omega\) körre. Ilyen kör létezik: gondoljuk meg, hogy az az \(\displaystyle e\)-re szimmetrikus kör, ami átmegy \(\displaystyle X\)-en és \(\displaystyle X\) \(\displaystyle \Omega\)-ra vett inverzén megfelelő lesz. Ha invertálunk erre az \(\displaystyle \omega\) körre, akkor \(\displaystyle X\) és \(\displaystyle \Omega\) helyben marad, így \(\displaystyle Y_1\) képe \(\displaystyle Y_2\) lesz és fordítva, hiszen érintő körök képei is érintő körök (valamint \(\displaystyle e\)-n fekvő félkörök képei is \(\displaystyle e\)-n fekvő félkörök lesznek). Mivel az inverzió kettősviszony tartó, valóban \(\displaystyle \|XY_1\|=\|XY_2\|\). \(\displaystyle \quad \square\)

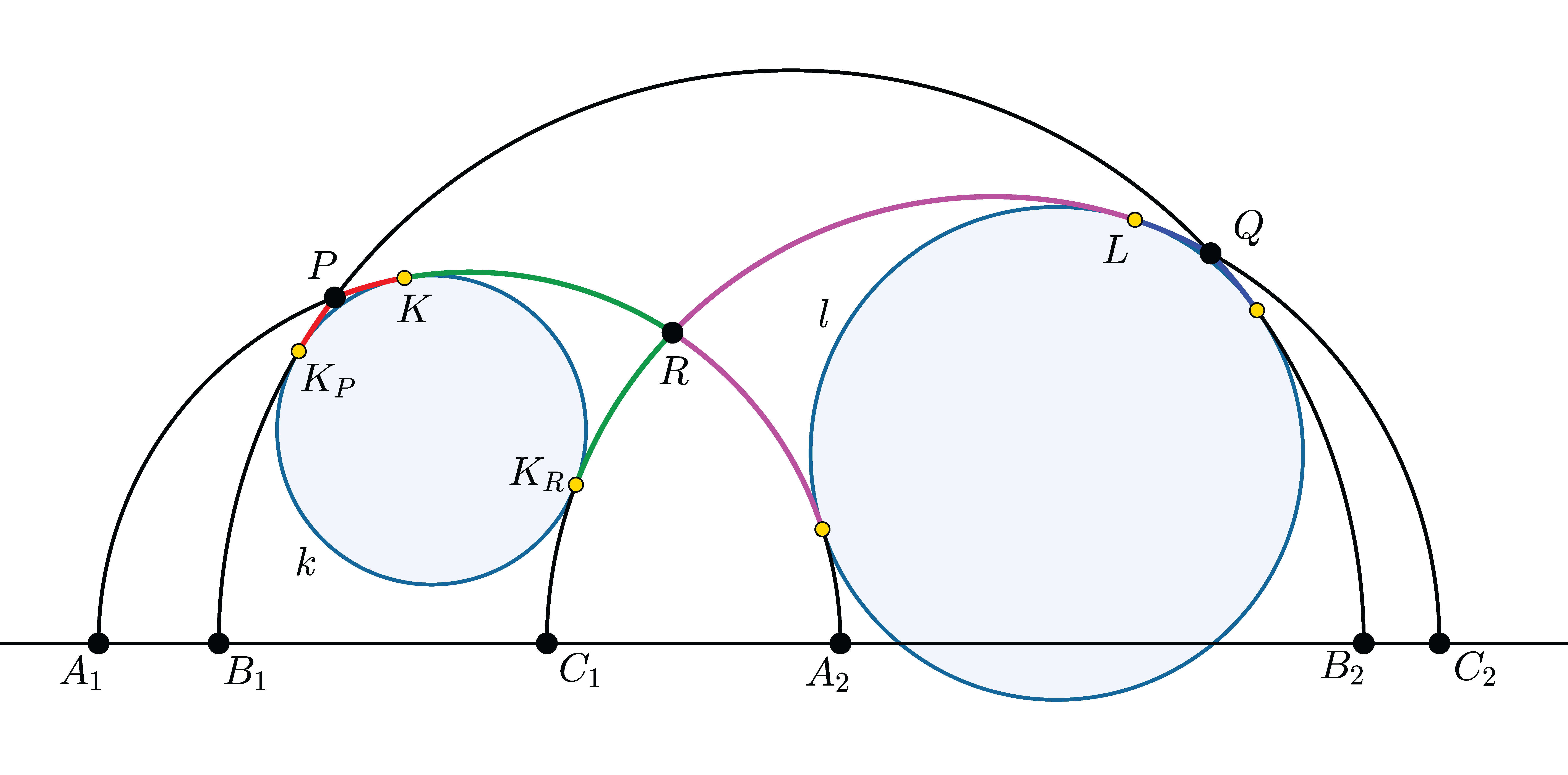
Most térjünk rá a bizonyítandó állításra. Azt kellene igazolni, hogy \(\displaystyle \|KR\|+\|LR\|=\|PQ\|\). Vegyük észre, hogy \(\displaystyle k\) és \(\displaystyle l\) éppen a \(\displaystyle PQR\) háromszög hozzáírt körei. És most ugyanaz működik, mint euklideszi geometriában: ha \(\displaystyle k\) a \(\displaystyle PQ\) egyenest \(\displaystyle K_P\)-ben, az \(\displaystyle RQ\) egyenest \(\displaystyle K_R\)-ben érinti, akkor a 2. Lemmának köszönhetően \(\displaystyle \|QP\|+\|PK_P\|=\|QR\|+\|RK_R\|\) , \(\displaystyle \|PK_P\|=\|PK\|\), \(\displaystyle \|RK_R\|=\|RK\|\), illetve \(\displaystyle \|PK\|=\|RK\|\). Ezekből könnyű számolással következik, hogy

\(\displaystyle \|KR\|=\dfrac{\|PR\|+\|PQ\|-\|QR\|}{2}.\)

Hasonlóan kapjuk, hogy

\(\displaystyle \|LR\|=\dfrac{\|PQ\|+\|QR\|-\|PR\|}{2}.\)

Innen pedig

\(\displaystyle \|KR\|+\|LR\|=\dfrac{\|PR\|+\|PQ\|-\|QR\|}{2}+\dfrac{\|PQ\|+\|QR\|-\|PR\|}{2}=\|PQ\|.\)

Ezt akartuk belátni.

Megjegyzés: Valójában hiperbolikus geometriával, pontosabban a félsík modellben oldottuk meg a feladatot azzal, hogy \(\displaystyle (s-b)+(s-c)=a\) (ahol \(\displaystyle s\) a félkerület, \(\displaystyle a,b,c\) az oldalak).

Statisztika:

2 dolgozat érkezett.
7 pontot kapott:	Varga Boldizsár.
6 pontot kapott:	Forrai Boldizsár.

A KöMaL 2025. májusi matematika feladatai